サーボシステムと位置制御
サーボ機構の目標値が位置や角度である場合, サーボ制御 / 位置制御と呼びます。
産業用ロボットアームの"関節の動き"を司る制御系は, この位置制御が基本となります。
今回は, タミヤ HighPower GearBox(DCモータ付き)に角度検出用の可変抵抗(ポテンショメータ)を取り付けたDCサーボシステムで制御実験を学習します。
なお, "ArduinoとMATLABで制御系設計をはじめよう!" 第5章の再現実験および評価レポートとなります。実験をして思ったこと, 自分なりにアレンジしたことなどをつらつらと書いていこうかと思います。
DCモータの速度制御系は, ステップ応答やシステム同定などを通して1次遅れ系であることが分かりました。角速度の積分が角度となりますので, 1次遅れ系に積分器を掛け合わせたような制御システムになることが前もって予想されます。いかにして, システムを把握し, 制御すべきでしょうか。
では, よろしくお願いします。
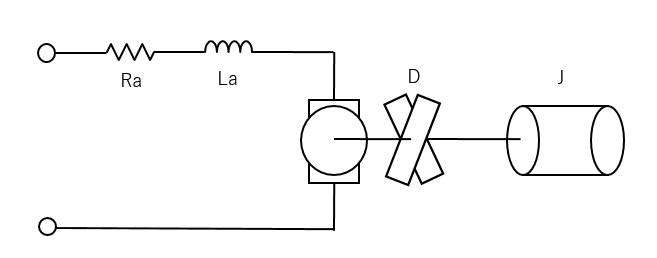
回路図:システム概観
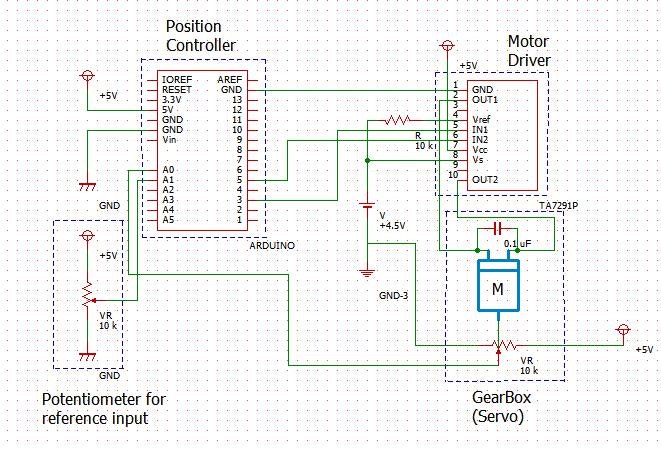
角度制御では, モータを正負両方回転する必要があります。モータを駆動するドライバについてですが, 手持ちでは東芝製 : TA7291Pが見つかりました。(現在生産中止のようですね...比較的新しいドライバを用いたかったのですが, ご勘弁を)
データシートの一部を抜粋します。
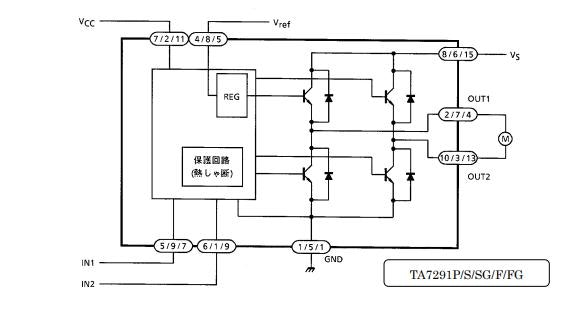
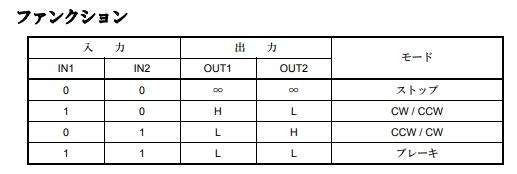
まとめると, IN1に5V, IN2に0Vを印加するとモータは正転し, IN1に0V, IN2に5Vを印加するとモータは逆転します。また片側の電圧に0V, もう片側にPWMを入力すると, デューティ比に応じてモータの回転速度を変えることができます。
角度検出部ですが, High Power Gearboxの出力ギア最上部のギアにポテンショメータ(可変抵抗)を取り付け, モータの出力角度に応じてポテンショメータも回転し, その時の5Vの分圧比によって角度を算出し, Arduino A0 入力端子のADCによって電圧を読み込み, 角度を計算します。DCモータは速度制御され, ギアボックスによって角度を出力し, ポテンショメータとADCをセンサとして, ギアボックスの軸の角度制御を行います。

ギアボックス, タミヤユニバーサルプレート, Arduino, 汎用シールドを一体化してみました。電装系とメカを一体化する部品が流行っているようにも感じます。
伝達関数
DCモータ入力電圧から角度までの伝達関数を求めていきたいと思います。
何度か説明させていただきましたが, DCモータの電気回路方程式
$$ R_{a}i(t) + L_{a}\frac{di(t)}{dt} + K_{e}\omega(t) = u(t)$$
上式にラプラス変換を適用すると,
$$ R_{a}I(s) + sL_{a}I(s) + K_{e}Ω(s) = U(s) $$
$$ I(s) = \frac{1}{sL_{a}+R_{a}}(U(s)-K_{e}Ω(s)) $$
となります。同様に, 回転運動方程式
$$ J \frac{d\omega(t)}{dt} + D\omega(t) = T(t) $$
に対してもラプラス変換を適用して, $Ω(s)$ でまとめると、
$$ Ω(s) = \frac{1}{sJ+D}\tau(s) $$
求まり, 角度と角速度に対しても,
$$ \theta(s) = \frac{1}{s}\omega(s) $$
と求めることができます。これらの関係式の入出力を関係づけることにより,下図のようなブロック図を得ることができます。
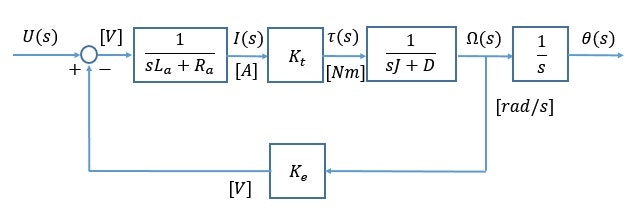
一般的にDCモータは機械系の運動方程式の応答より, 電気系の回路方程式の応答速度が速いです。また, 今回のHigh Power Gear Box付随のDCモータ(マブチ製 : RE-260RA)は, インダクタンスが小さいので $La ≃ 0$ と近似します。
$U(s)$ から $Ω(s)$ までの一巡伝達関数は,
$$ G(s)=\frac{Ω(s)}{U(s)} = \frac{\frac{K_{t}}{R_a}\frac{1}{Js+D}}{1+\frac{K_tK_e}{R_a}\frac{1}{Js+d}}
$$
$$ = \frac{K_t}{R_aJs+R_aD+K_tK_e} $$
$$ = \frac{\frac{K_t}{R_aD+K_tK_e}}{\frac{R_aJ}{R_aD+K_tK_e}s+1}$$
$$ = \frac{K}{Ts+1} $$
$$ K = \frac{K_t}{R_aD+K_tK_e}, T = \frac{R_aJ}{R_aD+K_tK_e} $$
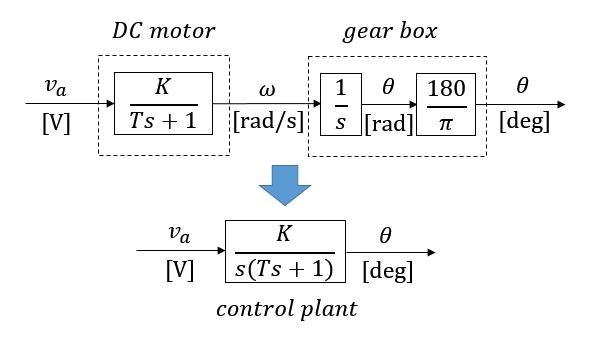
となります。ここで $K$ はゲイン, $T$ は時定数といいます。 したがって, モータ入力電圧 $U(s)$ から $θ(s)$ までの伝達関数は,
$$ θ(s)=\frac{1}{s}Ω(s)=\frac{K}{s(Ts+1)}U(s)$$
となります。このシステムは, 2次遅れシステムと呼びます。今回はこれを制御対象のシステムとします。(タコメータによる回転速度変換とギア比がありますが, どちらとも定数倍の係数が掛けられるので結局2次遅れです。また, †大部分の関節系は2次遅れ系で表されるのだそうです。)
制御対象のシステム同定
ステップ応答によってゲインや時定数を求めていきたいところですが,ポテンショメータの回転範囲が限られているため, 出力軸が最大角に達して止まります。
そこで, 制御プラントをフィードバックによって安定化させてそのあとにステップ応答実験を行い, パラメータを獲得していきます。
プラントの伝達関数を
$$ P(s) = \frac{K}{s(Ts+1)} $$
コントローラの伝達関数を
$$ C(s) = K_{P} $$
と置くことにより, 下図のフィードバック制御系の目標値 $r$ から出力 $y$ までの閉ループ伝達関数を求めてみます。
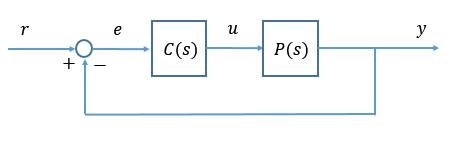
”前向き伝達関数”は, $r$から $y$ へ直線的にたどったときの伝達関数を掛け合わせたものなので $C(s)P(s)$ となり, また, 一巡伝達関数はフィードバックループを一巡した伝達関数を掛け合わせたものなので, これも $C(s)P(s)$ となります。
したがって $r$ から $y$ までの伝達関数は,
$$ G(s) = \frac{C(s)P(s)}{1+C(s)P(s)} $$
$$ =\frac{\frac{KK_p}{s(Ts+1)}}{1+\frac{KK_p}{s(Ts+1)}} $$
$$ = \frac{KK_p}{Ts^2+s+KK_p} $$
$$ = \frac{\frac{KK_p}{T}}{s^2+\frac{1}{T}s+\frac{KK_p}{T}} $$
となります。ここで,
$$ 2\zeta\omega_n = \frac{1}{T} , \omega_n^2=KK_p/T $$
と置くと, 以下の二次遅れシステムの伝達関数を得ることができます。
$$ G(s) = \frac{\omega_n^2}{s^2+2\zeta\omega_ns+\omega_n^2} $$
$\omega_n$は固有角周波数, $\zeta$は減衰比と呼ばれます。
この2次遅れシステムのステップ応答について, 逆ラプラス変換により
$$ y(t) = \mathcal{L}^{-1}[G(s)u(s)] $$
$$ =\mathcal{L}^{-1}[G(s)\frac{1}{s}] $$
$$ =\mathcal{L}^{-1}[\frac{\omega_n^2}{s^2+2\zeta\omega_ns+\omega_n^2}・\frac{1}{s}]$$
ここで $G(s)$ が極 $a_1$, $a_2$ を持つ場合,
$$ G(s)=\frac{a_1a_2}{(s-a_1)(s-a_2)} $$
となり,
$$ y(t) = \mathcal{L}^{-1}[\frac{a_1a_2}{(s-a_1)(s-a_2)}・\frac{1}{s}] $$
$$ y(t) = \mathcal{L}^{-1}[\frac{1}{s}+\frac{c_1}{s-a_1}+\frac{c_2}{s-a_2}] $$
$$ = 1 + c_1{e}^{a_1t} + c_2\mathrm{e}^{a_2t} $$
となり, $a_1$, $a_2$は$s^2+2\zeta\omega_ns+\omega_n^2=0$の極となります。
$ a_1,a_2 = -(\zeta±\sqrt{\zeta^2-1})\omega_n$
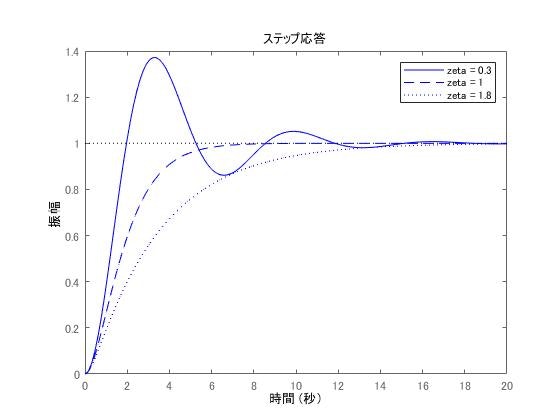
となります。上式より, $\zeta$ の大小により応答は変化します。
[1] $0<\zeta<1$ ... 不足減衰応答 応答は早いが振動的になる
[2] $\zeta=1$ ... 臨界減衰応答 振動せず目標値へ収束する
[3] $\zeta>1$ ... 過減衰 減衰が大きく, ゆっくりと応答する。
% second_sys.m
s = tf('s');
omega_n = 1;
zeta = 0.3;
P1 = omega_n^2/(s^2 + 2*zeta*omega_n*s + omega_n^2);
zeta = 1;
P2 = omega_n^2/(s^2 + 2*zeta*omega_n*s + omega_n^2);
zeta = 1.8;
P3 = omega_n^2/(s^2 + 2*zeta*omega_n*s + omega_n^2);
step(P1,'-',P2,'--',P3,':')
legend('zeta = 0.3','zeta = 1','zeta = 1.8')
% EOF of second_sys.m
出力が指令値を超えて行き過ぎることをオーバーシュートと呼び, 出力が最大になるときの時間 $T_p$ をオーバーシュート時間と呼びます。
それでは実験をしていきます。フィードバックで安定化させたうえで, ステップ応答の実験を行います。
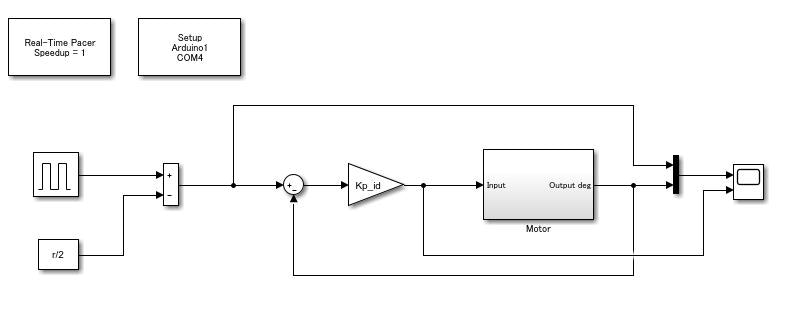
$K_p$ を多少振動するゲインを設定し, 数回分のステップ応答の平均応答を得ます。
% pos_id_step.m
% Initialize
close all
clear all
load sim_param
% Parameters for identification
r = 60;
r_cyc = 8;
Kp_id = 0.1;
Ncyc = 4;
tfinal = r_cyc*Ncyc;
% ID Experiment
open_system('pos_id_step_sl')
open_system('pos_id_step_sl/Scope')
sim('pos_id_step_sl')
% Data processing
y = yout.signals(1).values(:,2);
t = yout.time;
NN = length(y);
N = r_cyc/ts;
yy = reshape(y(2:NN),N,(NN-1)/N);
yf = yy(1:N/2,2:end); % 最初のデータを除き&前進データのみとする
% averaging and meaning
ym = mean(yf')';
y0 = ym(1); yN = ym(end);
ym = (ym-y0)/(yN-y0);
% Plot figure
t = (0:N/2-1)*ts;
figure(1)
subplot(211)
plot(t,yf), grid
xlabel('Time [s]'),ylabel('Output [deg]')
subplot(212)
plot(t,ym), grid
xlabel('Time [s]'),ylabel('Output [deg]')
% EOF of pos id_step.m
こうして得たステップ応答から, 2次遅れシステムの $\zeta$ や $\omega_n$ を求めていくことも考えられますが, 20ms 制御周期下におけるデジタル制御された応答では離散化の影響が大きくなります。
MATLABには最適化関数 fminsearch があります。これを使うと, 制約条件なしでの多変数関数の最小値が得られます。$K$ と $T$と実験で得たステップ応答データ $y[k]$ により, 2乗積分誤差
$$ J=\sum_{i=0}^{L-1}(y[k]-y_{sim}[k])^2 $$
を計算して return します。$y_{sim}[k]$ は制御対象をサンプリング間隔で離散化し, 比例ゲインでフィードバックしたうえで計算します。(離散化の影響を考慮します)
myfuncをfminserchから呼び出すと, $J$ が最小になる $K$ と $T$ を探してくれます。
function J = myfunc(x,y,t,ts,Kp_id);
K = x(1);
T = x(2);
P = tf([0 0 K],[T 1 0]); % P = K/(Ts^2 + s);
Pd = c2d(P,ts,'zoh'); % Discretization
Ld = Pd*Kp_id; % Loop transfer function
Gd = feedback(Ld,1); % Closed-loop system
ysim = step(Gd,t); % Step response
J = norm(y-ysim,2); % Error
function J = myfunc(x,y,t,ts,Kp_id);j
% pos_id_step_fit.m
% Parameter identification
Lt = input('Time length for fitting = ');
L = Lt/ts;
y_fit = ym(1:L);
t_fit = (0:L-1)*ts;
x0 = [500,0.5];
% Search parameters
xmin = fminsearch(@(x) myfunc(x,y_fit,t_fit,ts,Kp_id),x0);
% Plot figure
K_id = xmin(1);
T_id = xmin(2);
P = tf([0 0 K_id],[T_id 1 0]);
Pd = c2d(P,ts,'zoh');
Ld = Pd*Kp_id;
Gd = feedback(Ld,1);
ymodel = step(Gd,t);
figure(2)
plot(t,ym,'b-',t_fit,y_fit,'b*',t,ymodel,'r-');
xlabel('Time [s]'), ylabel('Output [deg]')
% Display results
fprintf('== Results ==\n')
fprintf('K = %f\n',K_id)
fprintf('T = %f\n',T_id)
% EOF of pos_id_step_fit.m
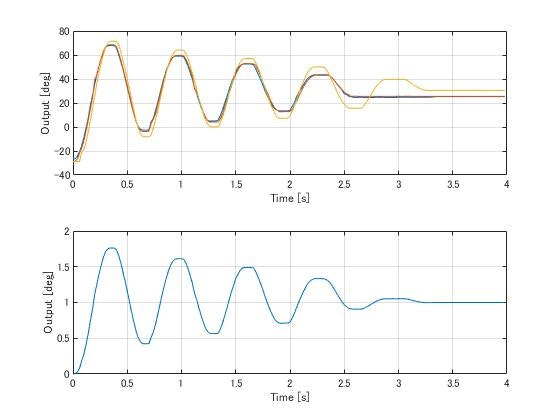
次に波形を示します。

0秒から1.8秒の間, $J$ を計算してもらいました。応答が収束するに従って, 非線形要素である静止摩擦があらわれます。これ以外にも配線の寄生インダクタンスや軸のねじれ, たわみなどの不確定要素が考えられますので, 完全な一致は難しいところです。
パラメータは
$K = 383.654357$
$T = 0.486207$
と得ることができました。
位置制御
得たパラメータで極配置などを行いたいですが, 簡潔にいきたいと思います。DCモータを速度制御する際には, PI 制御を用いました。
制御プラントの伝達関数とコントローラの伝達関数は,
$$ P(s) = \frac{K}{Ts+1} , C(s) = K_P + \frac{K_I}{s} $$
DCサーボを位置制御する際には, PD 制御を用いるといいでしょう。
制御プラントの伝達関数とコントローラ伝達関数は,
$$ P(s) = \frac{K}{s(Ts+1)} , C(s) = K_P + K_D s $$
前向き伝達関数 $C(s)P(s)$ は,
<速度制御>
$$ C(s)P(s) = (K_P+\frac{K_I}{s})・\frac{K}{Ts+1} $$
<位置制御>
$$ C(s)P(s) = (K_P+K_D s)・\frac{K}{s(Ts+1)} $$
$$ = (K_D+\frac{K_P}{s})・\frac{K}{Ts+1}$$
となり, 速度制御と位置制御で
$$ K_I⇔K_P , K_P⇔K_D $$
といった対応関係があることが分かります。位置制御をする際に, $K_P$ ゲインを偏差がなくなる程度に上げた後, $K_D$ ゲインをすこしずつ上げるといった手法で制御をしました。制御パラメータは,
$K_P = 0.12$
$K_D = 0.01$
で, 波形は以下のようになります。
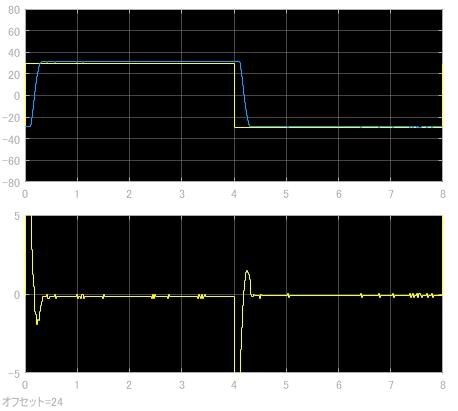
偏差が少し見られるものの, 一定角度に制御できているかと思います。
実験風景になります。
— まなお (@Manao0731) December 20, 2019
拙いですが, 以上で終わりに致します。ありがとうございました。(久しぶりに)DCサーボで位置制御しました。 pic.twitter.com/vqzgohK5Bv
— まなお (@Manao0731) January 26, 2020
参考文献
[1] 平田光男 ArduinoとMATLABで制御系設計をはじめよう!
お世話になっております。感謝です。
[2] 仮想制御研究室 理論と実践の架け橋 ~システム同定からモデル予測制御(PFC)~
[3] 足立修一 システム同定の基礎
[4] TA7291P データシート
[5] 荒木光彦 ディジタル制御理論入門
[6] 細田耕 実践ロボット制御