モデルベースデザイン
ArduinoとMATLAB/Simulinkを連携させてDCモータを速度制御してみる
http://manao55.hatenablog.com/entry/2019/09/11/232544
元の記事になります。
ArduinoとMATLAB/Simulinkを用いたDCモータのシステム同定
https://qiita.com/Manao/items/ed383a30bbe0c7b9534a
上記事の続きとなります。
実機を使った制御設計において, PIDゲインをいろいろ変化させながら実験を繰り返したり, ジーグラ・ニコルスの限界感度法といった持続振動条件を発見し, ゲイン設計を行うといった手法は, ”動き”を"推定"し"獲得"してゆくことになりますが, 時間がかかってしまうことが多いかと思います。
そのため, 制御プラントの数式モデルを獲得し, それに基づいて設計を行うモデルベース設計が行われることが望ましいと思われます。(システム制御の分野に限らず, 回路設計等広範な分野でも採用可かと)試行錯誤を伴う実験を回避したり, 仕様をみたす制御系設計が可能になったり, 新しい制御理論の実験検証がしやすくなります。製品開発期間の短縮, 問題の早期発見といったメリットもあります。
前回では, システム同定によって, 1次遅れ系制御対象(DCモータの速度制御系)のパラメータを同定し, 数式モデルを獲得しました。そこで今回は, 制御プラントの数式モデルを用いつつ, 制御特性の向上を狙って (なるべく簡単に) フィードバック制御設計を行います。
よろしくお願いします。
極配置法による制御ゲイン設計
ここでは, 閉ループ伝達関数の極を配置することによる”極配置法”によってPIゲインを決めていきます。
プラントの伝達関数を
$$ P(s) = \frac{K}{Ts+1} $$
PIコントローラの伝達関数を
$$ C(s) = K_{P} + \frac{K_{I}}{s} $$
と置くことにより, 下図のフィードバック制御系の目標値 $r$ から出力 $y$ までの閉ループ伝達関数を求めてみます。
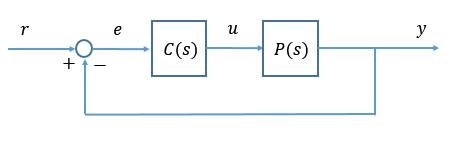
閉ループ伝達関数は以下の公式で計算できます。
$$ G(s) = \frac{C(s)P(s)}{1+C(s)P(s)} $$
上式分子は”前向き伝達関数”で, $r$から $y$ へ直線的にたどったときの伝達関数を掛け合わせたものなので $C(s)P(s)$ となり, また, 一巡伝達関数はフィードバックループを一巡した伝達関数を掛け合わせたものなので, これも $C(s)P(s)$ となります。
したがって $r$ から $y$ までの伝達関数は,
$$ G(s) = \frac{C(s)P(s)}{1+C(s)P(s)} $$
$$ =\frac{\frac{K}{Ts+1}(K_{P}+K_{I}/s)}{1+\frac{K}{Ts+1}(K_{P}+K_{I}/s)} $$
$$ = \frac{\frac{KK_{P}}{T}s+\frac{KK_{I}}{T}}{s^2+\frac{1+KK_{P}}{T}s+\frac{KK_{I}}{T}} $$
となります。
この伝達関数の, 分母式である,
$$ s^2+\frac{KK_{P}+1}{T}s+\frac{KK_{I}}{T} = 0 $$
の根が閉ループの極となります。極と $p1, p2$ が一致するようにゲイン設計をします。$p1$ と $p2$ を根に持つ方程式は,
$$ (s-p_1)(s-p_2) = s^2 -(p_1+p_2)s + p_1p_2 = 0 $$
上2式を比較すると, 次の式が得られます
$$ K_P = -\frac{(p_1+p_2)T+1}{K}, K_I = \frac{p_1p_2T}{K} $$
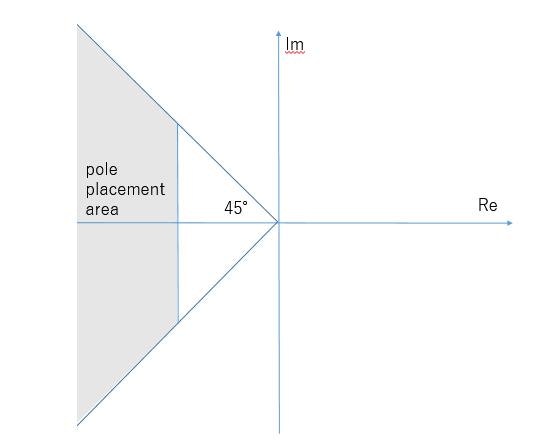
p1とp2は負の実数や共役複素数を設定します。
極と応答の理論背景についての考察, ,ステップ応答は, 逆ラプラス変換により
$$ y(t) = \mathcal{L}^{-1}[G(s)u(s)] $$
$$ \mathcal{L}^{-1}[G(s)\frac{1}{s}] $$
ここで $G(s)$ が極 $a_i$ を持つ場合,
$$ G(s)=\frac{n(s)}{(s-a_1)(s-a_2)...(s-a_n)}$$
となり,
$$ y(t) = \mathcal{L}^{-1}[\frac{c_0}{s}+\frac{c_1}{s-a_1}+\frac{c_2}{s-a_2}+...+\frac{c_n}{s-a_n}] $$
$$ = c_0+c_1\mathrm{e}^{a_1t} + c_2\mathrm{e}^{a_2t} + ... +c_n\mathrm{e}^{a_nt}$$
となり, 指数関数の和が応答になることが分かります。また, 極が虚部を持たなければ振動せず, 実部が絶対値の大きい負であれば応答は早く収束するイメージもつくかと思います。
前回の記事の手法でシステム同定を行いましたがパラメータは
$K : 1.02$
$T : 0.74$
となり, 波形は,
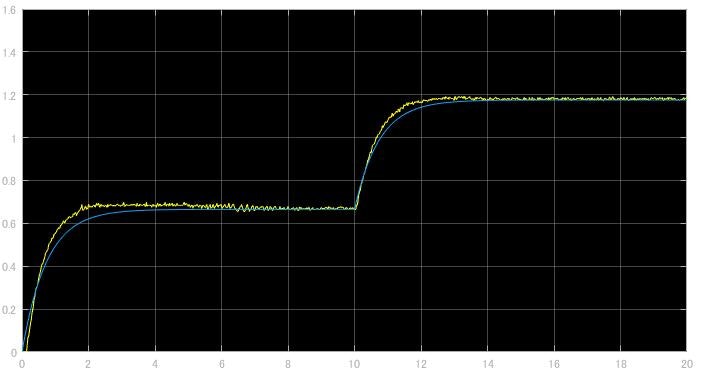
上図のような波形となりました。(すこしずれてしまいましたが...)では制御実験を行います。
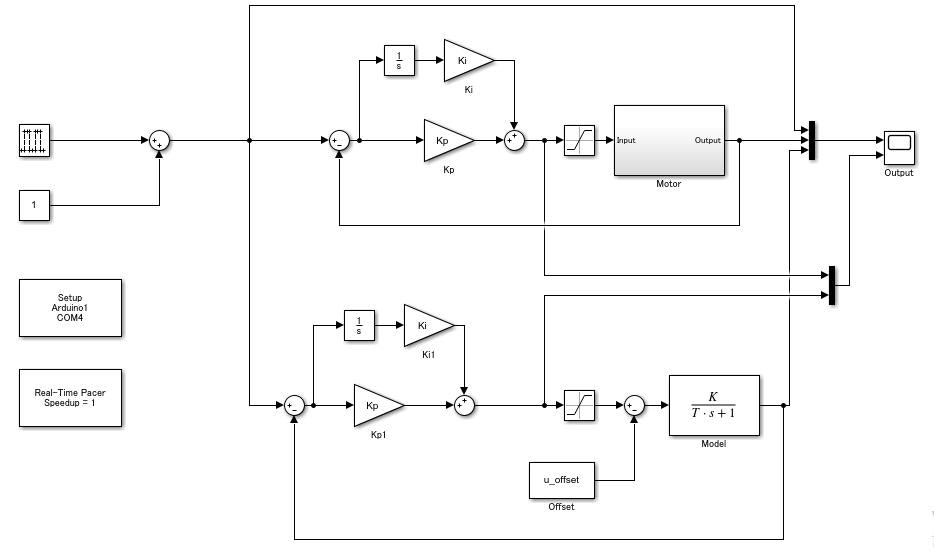
モータの電圧指令値を 1V 初期値, 0.5V 振幅のステップ電圧として, 制御器をPI制御器, 設定する極を-2の重根にした場合で実験を行いました。mファイルでSimulinkファイルを呼び出します。
% velo_pi_mbd.m
% Initialize & load data
close all
clear all
load model_data
% PI design by pole placement
p1 = input('p1 = ');
p2 = p1; % 重根の場合
% p2 = input('p2 = '); % p2も指定する場合
Kp = -((p1+p2)*T + 1)/K;
Ki = p1*p2*T/K;
% Open simulink model
open_system('velo_pi_mbd_sl');
open_system('velo_pi_mbd_sl/Output');
ts = 1/50;
sim('velo_pi_mbd_sl')
% EOF of velo_pi_mbd.m
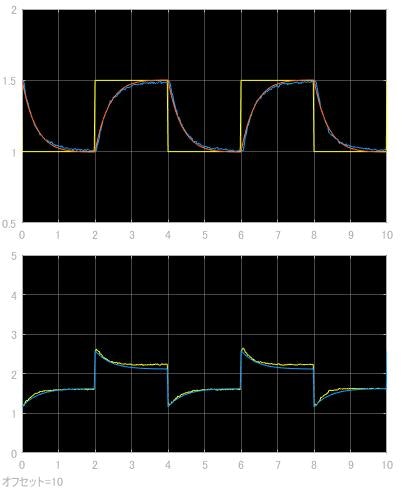
次に波形となります。上図で黄色が指令値,青が実機応答で, オレンジがシミュレーションによる数理応答になります。下図は青が指令値と数理応答の誤差, 黄色が実機応答と指令値の誤差になります。
$Kp = 1.92$
$Ki = 2.90$
$Kp = 3.37$
$Ki = 6.52$
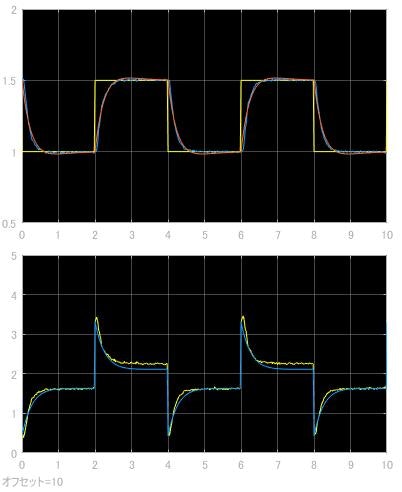
極を左半面に寄せるほど応答は早くなります。ちなみに $p1=p2=-4$ に設定すると,
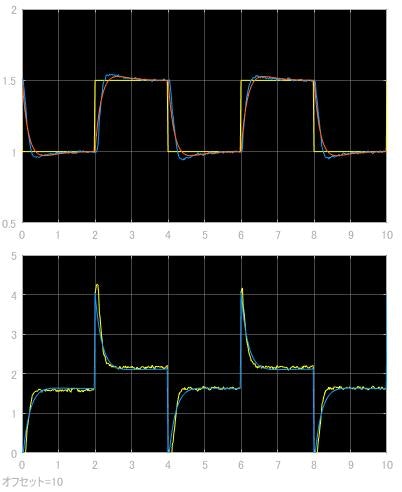
応答が早くなりましたが, オーバーシュートが生じます。PゲインもIゲインも増加しますので, 直感的にゲインを上げ続けると発振していきそうですね。(安定限界は調べていません)
$s$ 領域下における極配置設計, お手軽でなかなか良いと個人的に感じます。
今回 D 制御は入れていませんが, 古典制御におけるPID制御則はやはり偉大です。。。さすがこの世界を支えている制御則です。
z 変換とデジタル制御について
ATMega328Pというマイクロプロセッサを用いたArduinoでの実験を行いました。制御器は $s$ 領域における連続時間の下での設計でしたが, 本来マイコンが行っている計算は, 周期的に測定量をサンプリングし, デジタル回路のなかで計算を行ってから制御量を決定するので, その動作は断続的なものとなります。(デジタル制御と呼ばれる所以です)また, 今回のシステムは連続ダイナミクス(DCモータは連続時間において1次遅れ系)と離散ダイナミクス(デジタル論理のこと。コンピュータ, オートマトン)が混在したシステムのなので, ハイブリッド制御系と言ったりすることもできます。厳密にはデジタル制御器を実現し, 離散時間下で性能を評価したほうがよいですね。 離散信号を扱うのなら "$z$変換" を用いるのが便利です。
$k$を整数として,
$$ x(k)=0 (k<0) $$
を満たす $k$ の関数について,このような $x$ は数列
$$ {{x(0),x(1),x(2),...}}$$
を表し, $x(k)$ に対して $z$ の関数 $X(z)$ を
$$ X(z)=x(0)+x(1)z^{-1}+x(2)z^{-2}+...$$
$$
=\sum_{k=0}^{∞}x(k)z^{-k}
$$
で定義します。この(正則)関数を $x$ の $z$ 変換と呼びます。離散的時刻 $k$ に対して$z^{-k}$ を割り当てると解釈するといいでしょう。また数列 $x(k)$ に対応するインパルス列 $x(t)$ を
$$ x(t)=\sum_{k=0}^{∞}x(k)\delta(t-kT_{s}) $$
で, サンプリング信号を模擬します。時刻 $kT_s$ に発生する単位インパルス$\delta(t-kT_{s})$のラプラス変換は, $e^{-skT_{s}}$ であり, したがって $x(t)$ のラプラス変換 $X(s)$ は,
$$ X(s)= \mathcal{L}[x(t)]=\sum_{k=0}^{∞}x(k)e^{-skT_s} $$
となり, ここで,
$$ e^{sT_s} = z $$
と置き換えると. $X(z)$の右辺を得ることができます。つまり, 「インパルス列$x(t)$ の $z$ 変換は $x(t)$ のラプラス変換において $e^{sT_s}$ を $z$ で置き換えたもの」と解釈できます。この式から, $z$ が1ステップ(時間 $T_s$ )だけ信号を進める作用を持ち, $z^{-1}$ は1ステップだけ遅らせる作用をすることが示唆されます。
$e^{sT_s}$ について, 1次までのマクローリン展開より
$$ e^{sT_S} ≃ 1+sT_s $$
$e^{sT_s}=z$ と比較すると,
$$ \frac{1}{s} = \frac{T_s}{z-1} $$
と求めることができます。(前進オイラー法)
ちなみに, 双一次変換では
$$ \frac{1}{s} ≃ \frac{T}{2}\frac{z+1}{z-1}$$
といった変換となります。今回は簡易的に前進オイラー法でいきます。
PI制御器の伝達関数は $s$ 領域では,
$$ C(s)=K_p+\frac{K_i}{s}$$
ですが, マイコン側から見れば $z$ 領域におけるデジタル PI 制御器は,
$$ C(z)=K_p+K_i\frac{T_s}{z-1}$$
となります。
山谷サンプリングを想定して(Atmega328のサンプルホールドは違うかもしれません。後で調査します。), ADCがサンプリングしてからPWM出力するまでを1サンプリング遅延 $z^{-1}$ とすると, Simulinkファイルは次のようになります。

では, 全章で $s$ 平面上で設計した, $p=-3$ の時のゲインで実験したときの波形をそれぞれ見比べてみます。
$s$ 領域

$z$ 領域
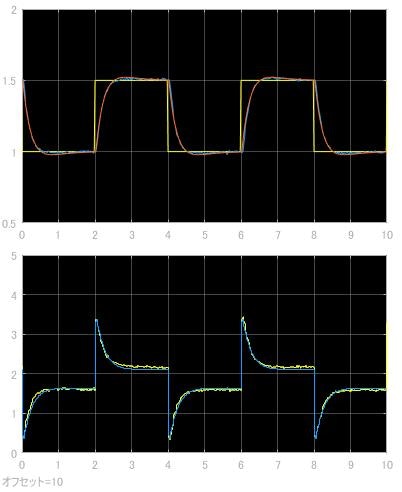
上図が $s$ 領域のPI制御器, 下図が $z$ 変換後の PI 制御器による実験波形とシミュレーション波形です。$z$ 変換した後のほうが数理応答に近づき, 誤差が少なくなっていることが分かりました。
これでさらに精密な実機評価が可能になったと思っています。
デジタル制御によって,
・$z$ 平面上の単位円で応答性や安定性を評価できる。
・数サンプルで制定する制御法(有限時間制定制御)が可能になる。
といった恩恵を得ることができます。z平面上で再設計したいところですが, 今回はここまででご勘弁を。(個人的に学生実験レベルでとどめておきたいのです。)
ちなみに実験風景は
このような感じです。test pic.twitter.com/FejzynGBaC
— まなお (@Manao0731) December 7, 2019
さらに性能を上げるには...
・デッドビート制御(有限時間制定制御, プラントも離散化して, 一巡伝達関数が n サンプル遅れと仮定して系を設計)
・モデル予測制御の導入(システム同定の恩恵により, プラントのパラメータが得られているため)
・完全追従制御 (堀藤本研究室グループの研究によく見受けられます)
(これらの制御法はAtmega328の演算性能が耐えられればの過程。コントローラの選定しなおしがあるかもしれません。ハードウェアサポートのあるマイコンボードが増えていくと個人的にうれしいです...)
・GaN-MOSFET, SiC-MOSFETなど低損失・高速応答デバイスとそのドライブ回路の導入 ( や み が ふ か い )
・ハイパーダッシュモーターやウルトラダッシュモーターへの移行
など考えています。
しばらくは電子デバイスやモータといったハードウェアの性能に頼らず, 制御ロジックを改善する方向で頑張っていこうと思います。(もともとの趣旨でもあります)
(80~90年代は繰り返し制御が, 昨今ではニューラルネットやディープラーニングなどが流行りましたが, FF的にパスを設けられないでしょうか)
また, FA-130RAを継続して使用していましたが, 実験を繰り返すうちに特性が悪化する傾向がありましたので, (ブラシ付きDCモータなので仕方ない部分はあります) 整流子がなく, ブラシ摩耗による制御悪化を受けにくいブラシレスDCモータによるベクトル制御にも挑戦したいと思っています。
簡易的ですが, ありがとうございました。
補足(前回分):DCモータの回路方程式, 運動方程式
DCモータの数式モデルを詳しく見ていきましょう。
下図のような, DCモータのプラントについて, 数式を追っていきます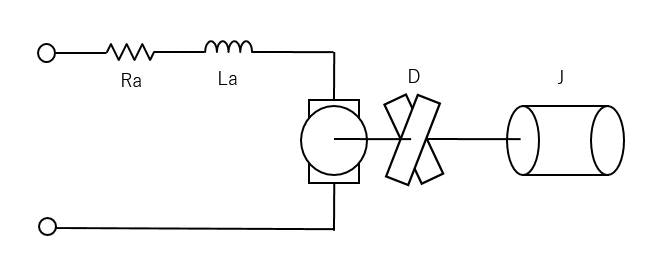
$Ra$ は巻き線抵抗, $La$ は巻き線のインダクタンスであり, モータへ電圧 $u$ を加えると電機子には電流 $i$ が流れます。モータは回転すると, それによって逆起電力が発生します。(手回し発電機と同じ原理です)逆起電力はDCモータの回転速度に比例します。
逆起電力定数を $K_e$, 電機子の回転各速度を $ω(t)$ とすると, $K_eω(t)$ と表すことができます。
抵抗での電圧降下 $R_ai(t)$, コイルの電圧降下 $L_a\frac{di(t)}{dt}$, モータの逆起電力 $K_eω(t)$ をすべて加えたものがモータの印加電圧 $u(t)$ と釣り合うので, 電気回路の微分方程式は,
$$ R_{a}i(t) + L_{a}\frac{di(t)}{dt} + K_{e}\omega(t) = u(t)$$
となります。DCモータに電流が流れると, トルクが生じます。トルクは電流に比例するので, 発生トルクを $Τ(t)$ とすると,
$$ T(t) = K_{t}i(t) $$
となります。$K_t$ はトルク定数と呼ばれます。
機械側の力学方程式に移りましょう。慣性モーメントが $J$, 粘性摩擦係数が $D$ の回転体にトルクがかかった出力側の回転運動方程式は下式のようになります。
$$ J \frac{d\omega(t)}{dt} + D\omega(t) = T(t) $$
モータの回転角度を $θ(t)$ とおくと, 回転角の時間変化が回転角速度となるので,
$$ \frac{d\theta(t)}{dt} = \omega(t) $$
となります。
補足(前回分):伝達関数
制御工学の理論を使って伝達関数を求めていきます。入力に対して何らかの因果を持って出力されるものをシステムと呼びます。その中で, 線形かつ時間特性が普遍なものを線形時不変システム(LTIシステム)と呼び, 伝達関数を求めることができます。
伝達関数は, 入力信号 $u(t)$ と, 出力信号 $y(t)$ をラプラス変換によって, 時間 $t$ の関数から $s$ 平面 $s$ の関数に変換したときの入力に対する出力の比です。
ラプラス変換は, 負期間において値が0となる時間関数 $f(t)$ に対して, 次のように定義されます。
$$ F(s) = \mathcal{L}[f(t)] = \int_0^∞ f(t)e^{-st}dt$$
$s$ は複素数を値に持つ変数です。例えば,
$$ \mathcal{L}[1] = \frac{1}{s}$$
微分公式は,
$$ \mathcal{L}[\frac{df(t)}{dt}] = sF(s) - f(0) $$
$f(0)$ は一般的に0と置くので, 微分関数のラプラス変換には, $s$ が微分の作用をしているとも取れます。$s$ は微分演算子と言われたりもします。では, DCモータの回路方程式
$$ R_{a}i(t) + L_{a}\frac{di(t)}{dt} + K_{e}\omega(t) = u(t)$$
上式にラプラス変換を適用すると,
$$ R_{a}I(s) + sL_{a}I(s) + K_{e}Ω(s) = U(s) $$
$$ I(s) = \frac{1}{sL_{a}+R_{a}}(U(s)-K_{e}Ω(s)) $$
となります。同様に, 回転運動方程式
$$ J \frac{d\omega(t)}{dt} + D\omega(t) = T(t) $$
に対してもラプラス変換を適用して, $Ω(s)$ でまとめると、
$$ Ω(s) = \frac{1}{sJ+D}\tau(s) , \tau(s) = K_{t}I(s) $$
求まり, 角度と角速度に対しても,
$$ \theta(s) = \frac{1}{s}\omega(s) $$
と求めることができます。これらの関係式の入出力を関係づけることにより,下図のようなブロック図を得ることができます。
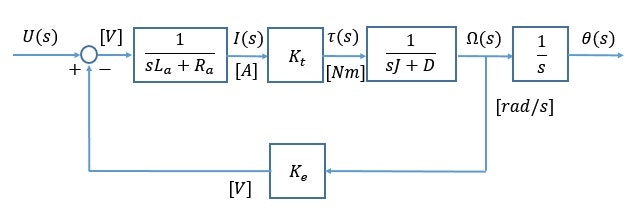
一般的にDCモータは機械系の運動方程式の応答より, 電気系の回路方程式の応答速度が速いです。また, 今回のDCモータ(マブチ製 : FA-130RA)は, インダクタンスが小さいので $La ≃ 0$ と近似します。(よくある仮定のようです)
$U(s)$ から $Ω(s)$ までの一巡伝達関数は,
$$ G(s)=\frac{Ω(s)}{U(s)} = \frac{\frac{K_{t}}{R_a}\frac{1}{Js+D}}{1+\frac{K_tK_e}{R_a}\frac{1}{Js+d}}
$$
$$ = \frac{K_t}{R_aJs+R_aD+K_tK_e} $$
$$ = \frac{\frac{K_t}{R_aD+K_tK_e}}{\frac{R_aJ}{R_aD+K_tK_e}s+1}$$
$$ = \frac{K}{Ts+1} $$
$$ K = \frac{K_t}{R_aD+K_tK_e}, T = \frac{R_aJ}{R_aD+K_tK_e} $$
となります。ここで $K$ はゲイン, $T$ は時定数といいます。 したがって, モータ入力電圧 $U(s)$ から $Ω(s)$ までの伝達関数は,
$$ Ω(s)=\frac{K}{Ts+1}U(s)$$
となります。このシステムは, 1次遅れシステムと呼びます。今回はこれを制御対象のシステムとします。(タコメータによる回転速度変換がありますが, 速度計側は回転速度と電圧が比例するので, 定数倍の係数が掛けられるので結局1次遅れです。)
参考文献
[1] 平田光男 ArduinoとMATLABで制御系設計をはじめよう!
Simulinkモデルとmファイルを参考にさせていただきました。お世話になっております。
今回の実験を通して多くの知識と経験を得させていただきました。感謝です。
[2] 仮想制御研究室 理論と実践の架け橋 ~システム同定からモデル予測制御(PFC)~
この人の書く文章が楽しみだったりします。
[3] 足立修一 システム同定の基礎
足立先生
[4] Atmega328 データシート
勉強します。
[5] 荒木光彦 ディジタル制御理論入門
古い本ですが参考になります。
[6] 2SK3234 データシート
手持ちのFETです。勉強します。
みなさまありがとうございます。