はじめに
最近, 機械学習, 深層学習の発展や社会実装に伴い, 数多くのAIベンチャーが目に移ります。主な適用先は, 自動運転車や産業用ロボット, バイオ分野で, 特に画像認識の応用が見受けられます。
ロボット・AIというワードをみると, 制御と学習の関連が連想されます。 ひとによって異なるのでしょうが, AIで動くロボットという概念はどこかにいる人類が考えていそうな欲のひとつなのかなと思われます。(ロボットが自律して判断して行動すると面白そうですよね)
制御と学習は昔から思いつく人は多いでしょうし, 始まりはなんだったのだろうかとふと思いました。近頃のロボティクスなどの研究では比較的新しい学習理論が適用されるとは思いますが, ここでは温故知新ということで, 個人的に学習と制御に関する初期の理論を調べてみて, 繰り返し制御のアイデアが興味を引いたので取り上げて確認しようと思いました。
繰り返し制御
繰り返し制御は, 東京工業大学制御工学科の井上 悳氏, 中野 道雄氏 およびに高エネルギー研 (現高エネルギー加速器研究機構)の久保 忠志氏, 松本 啓氏, 馬場 斉氏らにより陽子シンクロトロン加速器の電源の制御のために最初に考案されました。
井上 悳, 中野 道雄, 久保 忠志, 松本 啓, 馬場 斉, 陽子シンクロトロン電磁石電源の繰返し運転における高精度制御, 電気学会論文誌C, 1980, 100 巻, 7 号, p. 234-240
https://www.jstage.jst.go.jp/article/ieejeiss1972/100/7/100_7_234/_article/-char/ja
1周期 (試行) 前の偏差を利用して周期的な目標入力に高精度で追従させる制御系のようです。
当時は理論的に, またさまざまな分野への応用に関しての研究がなされていたようです。
原 辰次, 小俣 透, 中野 道雄, 繰返し制御系の安定条件と設計法, 計測自動制御学会論文集, 22 巻, 1 号, p.36-42
https://www.jstage.jst.go.jp/article/sicetr1965/22/1/22_1_36/_pdf
小林 史典, 原 辰次, 田中 啓友, 中野 道雄, 繰返し制御を応用したモータの回転むら低減法, 電気学会論文誌D, 107 巻, 1 号, p.29-34
https://www.jstage.jst.go.jp/article/ieejias1987/107/1/107_1_29/_pdf
ずいぶん昔の理論ではありますが, 理論的な考察も多く, 実応用に期待されていた制御法であったことは伺えます。採用するメリットとして,
・ロボットの繰返し動作など, 周期的な目標入力に対して有効である.
(閉ループ内に周期信号の発生機構をもつ繰返し制御系は,電源周波数やモータの回転
数に依存した周期的な外乱入力の除去にも効果がある.)
・逆システムの反復的生成法と考えられる学習制御方式は,ロボットの軌道制御などを実現する制御入力の自動生成の強力なひとつの方式である.
・数少ない日本人考案の国産の制御法である.
大元は加速器がターゲットでしたが, 1970年代ごろ複数の日本の企業が産業用ロボットの生産を開始したことにより, 反復作業の高性能化を狙った制御手法を求めていて, 学習制御のひとつとして注目され始めたのかなと推測しています。
加速器を安定に制御させて得たかった彼らの本当の目的についてはここでは触れないことにします。
繰り返し制御の構成
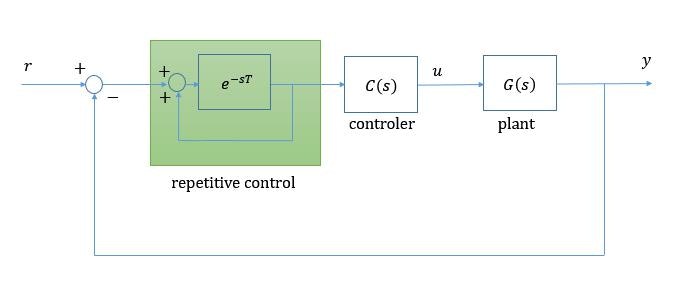
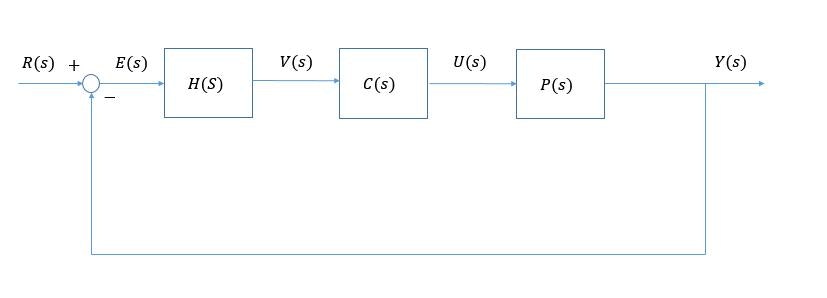
繰り返し制御の構成方法として様々な方法がありますが, 基本的な制御ブロックは以下のようになります。
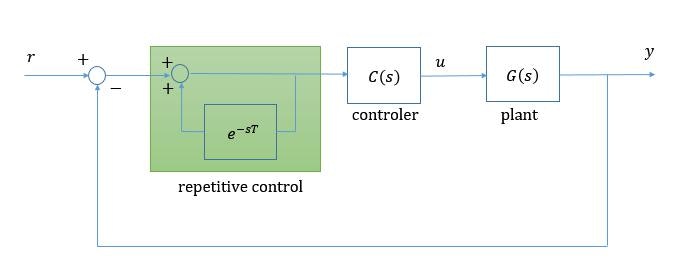
または $e^{-sT}$ のブロックをループ内の前向き伝達関数のブロックに配置して以下のようにもなります。
制御器 $C(s)$ の前段に設置されることが多いです。 二自由度制御のフィードフォワード制御部として扱われることがあります。
原理
繰り返し制御の原理について説明します。定式化の都合上, いくつか前提条件を設定します。
(ⅰ) 制御系の目標値 $r(t)$ は一定周期 $T$ を持つ繰返し信号か, あるいは一定値信号であるとする。
(ⅱ) この目標値のもとで, 波高値の有限な何らかの操作信号を制御対象に加えることにより制御偏差をなくすることが可能であるとする。
(ⅲ) 制御対象は線形であるとする。
前章のブロック図で示すような繰り返し制御器の伝達関数を $G_r(s)$ とすると,
$$
G_r(s)=\frac{e^{-sT}}{1-e^{-sT}}
$$
周波数応答は, $s → j\omega$ として,
$$
G_r(j\omega)=\frac{e^{-j\omega T}}{1-e^{-j\omega T}}
$$
(ⅰ) の仮定条件およびに上式より, $G_r(j\omega)$ は離散角周波数
$$
\omega_{k} = \frac{2\pi k}{T} (k=0,1,2,...)
$$
において各々一定の周波数成分を持ちます。(極を持ちます)
このとき, 周波数成分は
$$
|G_r(j\omega_k)|→\infty, \omega=\omega_k
$$
となり, 利得が無限大に近づくことが分かります。
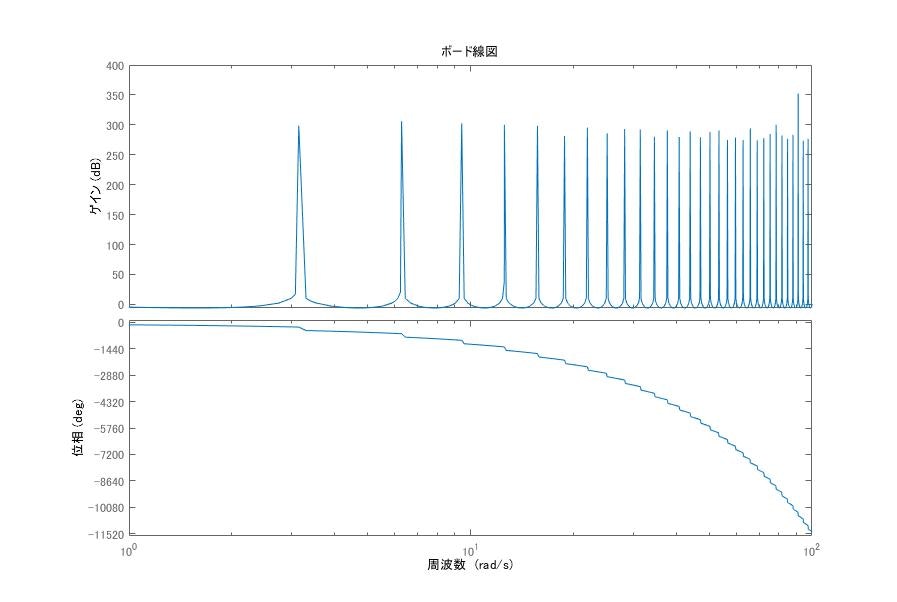
以下に繰り返し制御部の周波数応答を示します。
% repete_bode.m
s = tf('s');
T = 2; % 2秒の周期関数の発生機構
G = exp(-s*T)/(1-exp(-s*T));
bode(G);
このため, 制御系が安定で, $|C(s)G(s)|$ が有限の周波数で零にならず, 外乱 $ d(t) $ が一定値あるいは $T$ の整数分の1の周期を持つとき、偏差は零へ収束します。
例えば外乱がないとき, 閉ループ伝達関数 $G_{close}(j\omega) $ は,
$$
G_{close}(j\omega_k)=\frac{G_{r}(j\omega_k)C(j\omega_k)G(j\omega_k)}{1+G_{r}(j\omega_k)C(j\omega_k)G(j\omega_k)}=\frac{C(j\omega_k)G(j\omega_k)}{\frac{1}{G_r(j\omega_k)}+C(j\omega_k)G(j\omega_k)}→1
$$
1 に収束するので, 偏差が零へと収束していきます。
サーボ系の重要な要件である内部モデル原理 (前向き伝達関数のいずれかに目標値の伝達関数が含まれれば定常偏差が0になる) がこの場合でも成立するのであれば, 周期関数の発生機構を制御ループ内に挿入することで, 周期 $T$ の任意の周期目標入力に対して定常偏差をなくすことができます。
強引な式変形ですが,
$$
e^{-sT}≃\frac{1}{1+sT}
$$
と近似すると,
$$
\frac{e^{-sT}}{1-e^{-sT}}≃\frac{1/(1+sT)}{1-1/(1+sT)}=\frac{1}{sT}
$$
と表してみると, 周期関数の発生機構自体が(ゆっくりとした)近似的な積分器として解釈することもできます。
Iコントローラ $k_i/s$ やPIコントローラ $k_p+k_i/s$ などをかんがみると, 1形の制御系と繰り返し制御系とは
$$
\frac{k_i}{s} → \frac{e^{-sT}}{1-e^{-sT}}, k_p → α
$$
といった対応があることが分かります。
以下の図において, 単純に周期関数発生機構 $e^{-sT}/(1-e^{-sT})$ だけでなく $α$ を並列に接続し, PI制御器を模したような繰り返し補償器としての構成も考えることができます。この構成を, 修正繰り返し制御系とも呼びます。
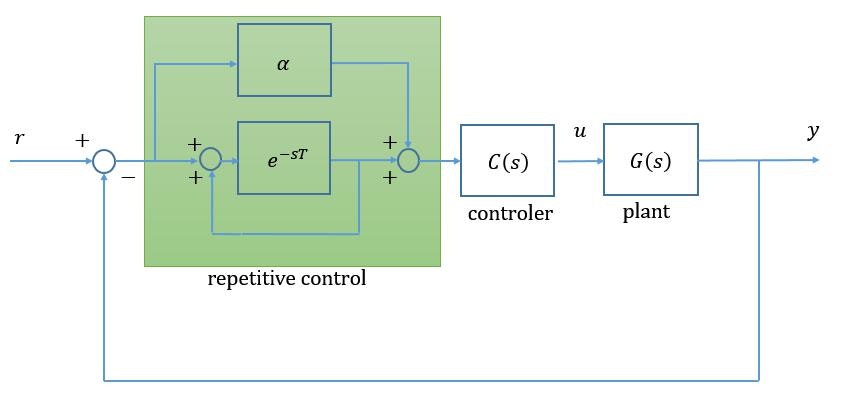
初めの繰り返し制御のブロック図は $ \alpha= 1 $ としたときに対応することとなります。
PI制御器と繰り返し制御器はよく似ていますが, 前者が有限次元システムであるのに対して, 繰り返し制御はむだ時間 $T$ をもつ無限次元システムである点が異なります。(次数を問いません)
この性質は制御の安定性を議論する際に特殊な側面が表れてきます。
繰り返し制御の安定条件
$$
E(s) = R(s) - Y(s) ... (1)
$$
$$
Y(s) = G(s)V(s) + Y_{0}(s) ... (2)
$$
$$
V(s) = \alpha E(S) + W(s) ... (3)
$$
$$
W(s) = e^{-sT}{W(s)+E(s)} + W_{0}(s) ... (4)
$$
が成立します。($Y_{0}(s)$, $W_{0}(s)$はそれぞれG(s), $e^{-sT}$ の初期値応答のラプラス変換である。)
これらの関係を用いると, $(1)$, $(4)$ 式より
$$
(1-e^{-sT})E = (1-e^{-sT})(R-Y) ... (1)'
$$
$$
(1-e^{-sT})W = e^{-sT}E + W_{0} ... (4)'
$$
が成立します。ここで, (2), (3), (4) 式より,
$$
(1-e^{-sT})Y = (1-e^{-sT})(GV+D+Y_{0})
$$
$$
= (1-e^{-sT})(\alpha GE+GW+D+Y_{0})
$$
$$
= (1-e^{-sT})\alpha GE + e^{-sT}GE + GW_{0} + (1-e^{-sT})(D+Y_{0}) ... (5)
$$
が導かれ, $(1)'$に$(5)$を代入すると,
$$
(1-e^{-sT})E = (1-e^{-sT})R-(1-e^{-sT})\alpha GE - e^{-sT}GE - GW_{0} - (1-e^{-sT})(D+Y_{0})
$$
つまり,
$$
(1+\alpha G)E = e^{-sT}[1+(\alpha-1)G]E + D_{e}
$$
$$
E = e^{-sT}[1+\alpha G]^{-1}[1+(\alpha-1)G]E+[1+\alpha G]^{-1}D_e ... (6)
$$
となります。ここで,
$$
D_{e}=(1-e^{-sT})R-(1-e^{-sT})Y_{0}-GW_{0} ... (7)
$$
となります。
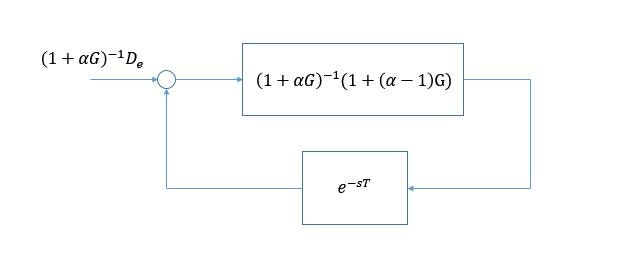
$(7)$ 式の関係をブロック線図で表すと, 以下の等価系が得られます。
ではこの図の等価系の入出力条件から、繰り返し制御系の安定条件を求めてみましょう。
$$
r_0(t) = \mathcal{L}^{-1}[(1-e^{-sT})R(s)] ... (8)
$$
$$
d_0(t) = \mathcal{L}^{-1}[(1-e^{-sT})D(s)] ... (9)
$$
とおいて
$$
r_{0}(t) = 0, d_0(t) = 0; t>=T
$$
と定義します。 $ 0<=t<=T $ で $ r(t) $ , $ d(t) $ が有界であるならば,
$ r_{0}(t) ∈ L_2 $ , $ d_{0}(t) ∈ L_2 $ となります。
($ L_2 $ は $‖f‖^2_{L2} = \int_{0}^{\infty}f(t)^2dt < \infty$ でノルムが定義される [0,∞]上の加速関数 $f(t)$ の集合です)
ここで, $ [1+\alpha G(s)]^{-1} $ の漸近安定性($t→\infty$ で平衡点 $X_e$ に収束)を仮定すると, $(7)$式より,
$$ \mathcal{L}^{-1}[(1-e^{-sT})D_{e}(s)] ∈ L_2 ... (10) $$
となります。等価系の閉ループにおいてスモールゲイン定理を用いると,
$$
|[1+\alpha G(s)]^{-1}[1+(\alpha-1)G]|<1 ... (11)
$$
が成立します。
$(10)$,$(11)$ の仮定の下, 有界で連続な周期信号 $ r(t) $, $ d(t) $ に対して
$$
e(t) = \mathcal{L}^{-1}[E(s)] ∈ L_2
$$
が成立し, 繰り返し制御の定理となります。
$(11)$ 式の考察について, $(11)$ 式は,
$$
[1+\alpha G(j\omega)]^{-1}[1+(\alpha-1)G(j\omega)][1+(\alpha-1)G^{*}(j\omega)][1+\alpha G^{}(j\omega)]^{-1}<1
$$
$$
[1+(\alpha-1)G(j\omega)][1+(\alpha-1)G^{}(j\omega)]<[1+\alpha G(j\omega)][1+\alpha G^{}(j\omega)]
$$
$$
G(j\omega) + G^{*}(j\omega) + (2\alpha-1)G^{*}(j\omega)G(j\omega)>0
$$
と変形することができ,
$$
\gamma = \frac{1}{2\alpha-1}
$$
と置くと, 以下のように場合分けすることができます。
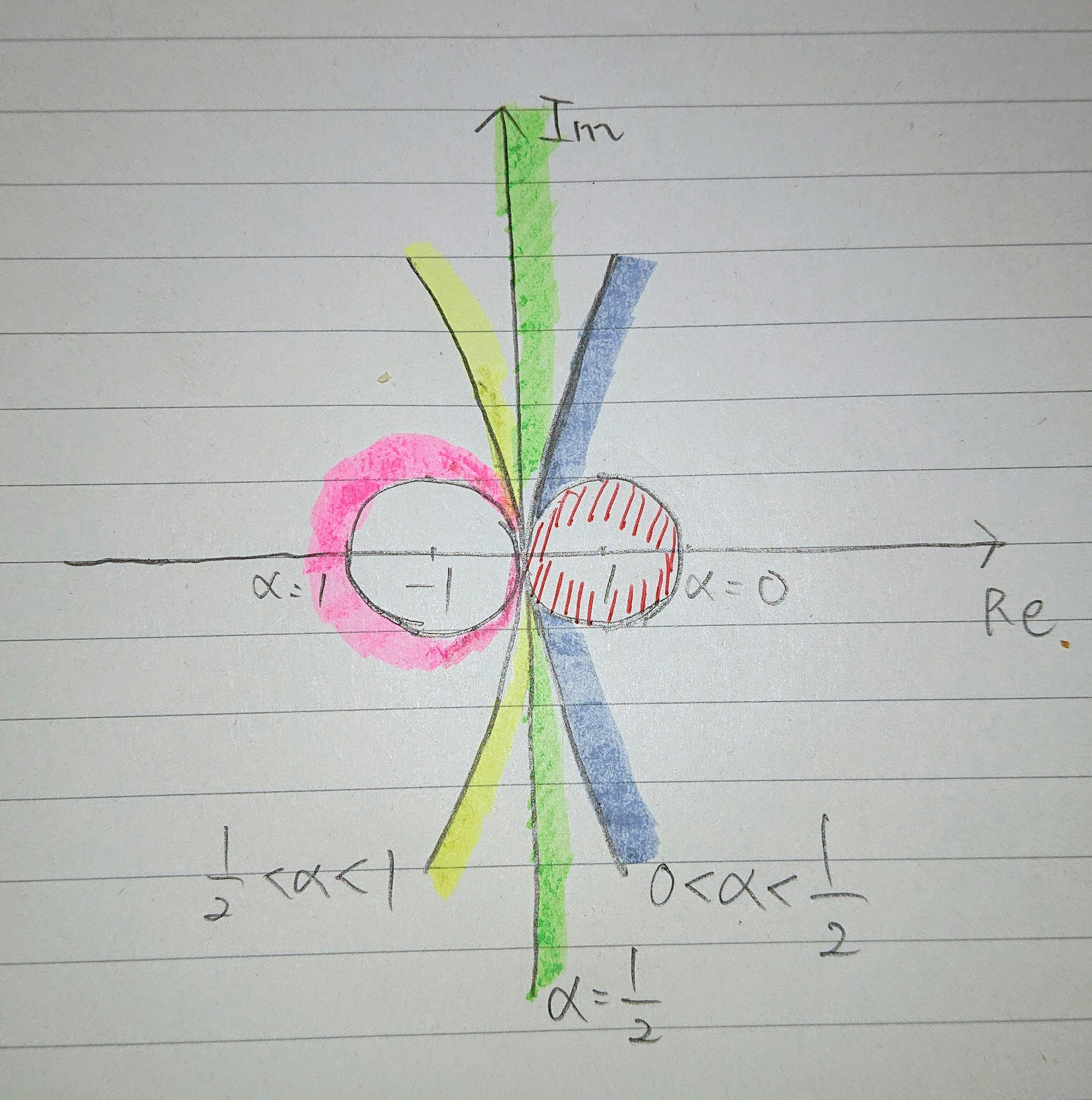
$1)$ $\gamma>0(\alpha>1/2)$ のとき,
$$
|G(j\omega)+\gamma|>\gamma ... (12)
$$
$2)$ $ \gamma = \infty (\alpha=1/2)$ のとき,
$$
G(j\omega)+G^{*}(j\omega) > 0 ... (13)
$$
$3)$ $\gamma<0 (\alpha<1/2)$ のとき,
$$
|G(j\omega)+\gamma|>-\gamma ... (14)
$$
と導くことができます。特に $ \alpha = 1 $ のとき, 最適制御やカルマンフィルタの最適性条件 (円条件) と等しくなります。以下にナイキスト線図を示します.(すみません.手書きですが)
繰り返し制御の設計法
当時, 繰り返し制御などの学習制御の収束条件についても最適制御の最適性条件との関係性が考察されており, 状態フィードバックによる設計法が提案されています。
川村 貞夫, 宮崎 文夫, 有本 卓, 学習制御システムのシステム論的考察, 計測自動制御学会論文集, 21 巻, 5 号, p.445-450
https://www.jstage.jst.go.jp/article/sicetr1965/21/5/21_5_445/_pdf/-char/ja
個人的にはあまり本質的な場面ではない(は?)と思ってしまったので, ここでは出力動的フィードバックによる繰返し制御系の設計法をなるべく簡単に事実だけ述べて説明します。
プラント $ P(s) $ が与えられたとき, $ G(s) = C(s)P(s) $ が
$$
[1+\alpha G(s)]^{-1} : 漸近安定
$$
$$
|G(j\omega)+1/(2\alpha-1)|>1/(2\alpha-1) (\alpha>1/2) ... (15)
$$
の二つの条件を満たす補償器 $ H(s), C(s) $ の設計法について検討します。
ここではカルマンフィルタと完全制御の手法を用いた最小位相系に対する修正繰り返し制御の設計法 $ (\alpha = 1) $ を説明します。
まず, $ P(s) $ を最小実現 $(A_p,B_p,C_p) $ を用いて,
$$
P(s) = C_p(sI-A_p)^{-1} B_p
$$
と置きます。このとき, $ C(s) $ を 以下の図のように構成します。

このとき, $ G(s) = (C(s)P(s)) = Y(s)V(s)^{-1} $ は,
$$
G(s) = [C_p (sI-A)^{-1}-C_p(sI-A_p+BK)^{-1}]*[I+FC_p(sI-A_p+B_p K)^{-1}]^{-1} F ... (16)
$$
と表せます. ここで, $ K $ を完全制御のアルゴリズム†(補足)で求め, それを $ K_p $ を表すと
$$
\lim_{\rho \to \infty} C(sI-A_p+B_p K \rho)^{-1} = 0
$$
が成立します。これを $(16)$ 式に適用すると,
$$
\lim_{\rho \to \infty} G(s) = C_p (sI - A_p) F
$$
このとき, $F$ はカルマンフィルタのゲイン
$$
F = \beta \sum C_{p}^{T}
$$
$ \phi $ : 非負定, $ (\phi^{1/2},A_p) $ : 可観測対という条件で, $ \sum $ はリカッチ方程式
$$
A_p \sum + \sum A_p^{T} + \phi - \sum C_p^{T} C_p \sum = 0
$$
で定めるとすると, ロバスト性不等式
$$
(1+1/\beta G_\infty(j\omega))(1+1/\beta G_\infty^{*}) > 1
$$
つまり
$$
|G_\infty(j\omega) + \beta| > \beta
$$
が成立します。したがって,
$$
2\alpha-1>1/\beta ... (17)
$$
と設定すれば, $\rho → \infty$ で $ G(s)$ は $\omega=\infty$ を除いて漸近的に式 $(12)$ を満たします。
この時, $(17)$ 式より,
$$
\alpha \beta> (1+\beta)/2 > 1/2 ... (18)
$$
であるので, カルマンフィルタのゲイン減少に関する安定余裕が $1/2$ であることを用いると, 式 $(10)$ 式が成立することが確かめられます。
これまでの議論をまとめると, 漸近的設計法は以下のようにまとめられます。
$1)$ $ P(s) $ の最小実現 $ (A_p, B_p, C_p) $ を求める.
$2)$ $ C(s) $ を図のように構成し, ゲイン $ F $ と, $ K $ を以下のように決める。
$F$ : カルマンフィルタのゲインの $ \beta $ 倍
$K$ : 完全制御のゲイン $ K_\rho $
$3)$ 式 $(17)$ を満たすように $\alpha$, $\beta$ を決定する。
あとがき
正直自分で書いていてこれだけでは自分がよくわかってないなと思ったので(???), 具体的なプラントを使って制御する様子を Matlab/Simulink advent Calender 4日目の記事で書いてみました。ご興味ありましたらご覧ください。
外乱オブザーバと繰り返し制御を併用した単軸アームの学習制御
https://qiita.com/Manao/items/cb8c0ab05cee98e6fde3
(補足)完全制御について
線形システム
\begin{align}
x &= Ax+Bu \\
y &= Cx
\end{align}
を考える。ここで $x$ は $n$ 次元状態ベクトル, $u$ は, $r$ 次元入力ベクトル, $y$ は $m$ 次元出力ベクトルで, $A$, $B$, $C$ は適当なサイズの定数行列であります。上システムは、可制御・可観測であるとします。評価関数
$$
J=\int_{0}^{\infty}(y^{T}Qy+u^{T}Ru)dt, Q>0,R>0
$$
に対する最適レギュレータは, 状態フィードバック
$$
u=K_{opt} x, K_{opt} = -R^{-1}B^T P
$$
で与えられます。ただし $P$ はリカッチ方程式
$$
PA+A^T P-PBR^{-1}B^T P+C^T QC=0
$$
の正定解です。最適還送差行列を
$$
T_{opt}(s)=I-K_{opt}(sI-A)^{-1} B
$$
で定義すると, $T_{opt}(s) $ は不等式
$$
T_{opt}^{*}(j\omega) \ \ R\ \ T_{opt}(j\omega) > 0
$$
を満足することが知られています。上式は安定余裕や感度改善などの最適レギュレータのロバスト性にかんする議論の基礎を与えるもので, ロバスト性不等式と呼ばれます。
カルマンフィルタのロバスト性不等式も双対性を用いれば導かれます。つまり,
$$
F_{opt}=-P_{k} CR_{k}^{'}
$$
$$
AP_k+P_kA^T-P_kC^TR_k^{-1}CP_k+BQ_kB^T=0
$$
で与えられるカルマンフィルタゲインに対して, 最適還送差行列を
$$
T_{k \ \ opt}^{*}(s)=I-C(sI-A)^{-1} F_{opt}
$$
で定義すると, $T_{opt}(s) $ は
$$
T_{k \ \ opt}(j\omega) R_k T_{k \ \ opt}^{*}(j\omega)-R_k>0
$$
を満足します。ここで, $Q_{k}>0$, $R_k>0$ はそれぞれ外乱, 観測雑音の共分散行列である。
完全制御について, 必要な結果を述べます。パラメータ $\rho$ を含む状態フィードバックの族
$$
u=K_{\rho} x
$$
を考えます。ただし $\rho$ はゲイン行列の各要素に有利関数として含まれる。 $K_{\rho}$ が
$$
\lim_{\rho \to \infty} \int_{0}^{\infty}||C_{e}^{(A+BK_{\rho})t}||^{2} dt = 0 ... (20)
$$
を満足するとき, $K_{\rho}$ はシステムに対して完全制御を達成するといいます。
以下 $\rho→\infty$で閉ループ系の極が次の条件を満足する場合を考えます。
[A] $A+BK_{\rho}$ のすべての固有値(状態フィードバックのもとでの閉ループ極)は次の2つの条件のうちいずれかを満足する。
(i) $ \lim_{\rho \to \infty} \lambda_i (A+B K_{\rho}) = r_i $
(ii) $ \lim_{\rho \to \infty} \rho^{-1} \lambda_i (A+B K_{\rho}) = r_i$
ただし $r_i$ は負の実部を持つ複素数である。仮定[A]のもとで関係(20)は等価な周波数値域における条件
$$
\lim_{\rho \to \infty} C(sI-A-BK_{\rho})^{-1} = 0
$$
$$
\lim_{\rho \to \infty} C(\rho sI-A-BK_{\rho})^{-1} = 0
$$
に置き換えられます。完全制御の存在条件は次のように与えられます。
[命題1]
$ K_{\rho} → (C,A,B) $ を満足する $K_{\rho}$ が存在するための必要十分条件は, システム(C,A,B)が右可逆で最小位相系(すべての零点の実部が負)であることです。
完全制御の双対は完全観測です。完全観測は$ F_{p}^{T}→(B^{T},A^{T},C^{T})$ を満足するオブザーバゲインの族 $F_{p}$ によって定義される。つまり恒等オブザーバ
$$
z = (A+F_p C)z-F_p y + B u
$$
は, (20)式に対応した関係
$$
\lim_{\rho \to \infty} \int_{0}^{\infty}||C_{e}^{(A+BF_{\rho})t}||^{2} dt = 0 ... (21)
$$
を満足します。[A]と同様の仮定の下で (21)式は周波数領域における条件
$$
\lim_{\rho \to \infty} C(sI-A-F_{\rho}C)^{-1} B = 0
$$
$$
\lim_{\rho \to \infty} C(\rho sI-A-BF_{\rho})^{-1} B
= 0
$$
と等価になります。完全観測を$F_p → (C,A,B) $ と書きます。完全観測の存在は[命題1]で右可逆を左か逆に置き換えたものであります。