TensorFlowを自習した事を忘れない様にするためのメモです。 TensorFlow の チュートリアルや入門書に掲載されているサンプルコード元にして、独自に訓練データを乱数で作成して、線形回帰と非線形回帰の問題を修正したコードで解いたものです。 TensorFlowの初心者で間違いを含むかもしれませんので、もし間違いを発見したら教えていただけると幸いです。
TensorFlow実行環境
TensofFlowの実行環境は、MacOSにDockerCEをインストールして、コンテナのJupyter Notebookを利用しました。 これは、とても簡単に、Jupyter notebook を利用することができます。
MacのDockerCEのインストールは参考資料[3]を参照しました。また、Jupyter Notebookは DockerHubに登録されているコンテナ jupyter/tensorflow-notebook 参考資料[4] を利用しました。
Juypter Notebookの起動方法
DockerCEの実行環境ができたら、次のコマンドを実行してJupyter Notebookを起動します。
docker run -it --rm -p 8888:8888 jupyter/tensorflow-notebook
起動が完了すると、URLアドレスと次の様なメッセージが表示されるので、ブラウザでアクセスして、利用を開始します。
[C 02:22:41.514 NotebookApp]
Copy/paste this URL into your browser when you connect for the first time,
to login with a token:
http://localhost:8888/?token=56b93c77abe72760dbab8afb4fc7510861142722973d801f
線形回帰
トレーニング・データの作成
Jupyter notebook を使って、乱数で 配列 x_data を作って、次の式で 配列 y_data を作ります。
$$ y = 3x + 2 $$
これだけだと、綺麗すぎて現実のデータっぽく無いので、乱数を使って、配列 y_dataにノイズを加えておきます。
import numpy as np
import matplotlib.pyplot as plt
# データを生成
n=10
x_data = np.random.rand(n).astype(np.float32)
y_data = x_data * 3 + 2
# ノイズを加える
y_data = y_data + 0.15 * np.random.randn(n)
# ノイズ付きデータを描画
plt.scatter(x_data,y_data)
plt.show()
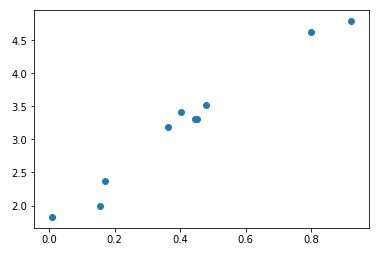
次の図は、上記のコードの実行結果です。 このデータを訓練データとして、TensorFlow で線形回帰分析を実行します。
線形回帰モデルと最適化対象のインスタンス化
次の式のWとbの最適値をTensorFlowを利用して求めていきます。
$$ y = W * x + b $$
この最適化対象の変数WとbをTensorFlowのtf.Variableクラスのインスタンスとして定義します。
そして、トレーニングデータとWとbを使って、線形回帰モデルの式をPythonのコードで表現します。
W = tf.Variable(tf.zeros([1]))
b = tf.Variable(tf.zeros([1]))
y = W * x_data + b
損失関数 (誤差関数)の定義
TensorFlowは訓練の過程で、その段階のWとbの値か得られる計算結果と、訓練データとの差を評価して、最も差が小さくなる様に、Wとbの変数を調整していきます。この誤差を計算する式は、次の最小二乗法の手法に従った式を用いてTensorFlowで表現します。
$$ E = \frac{1}{N} \sum_{i=1}^{N} (y_{i} - yt_{i})^2 $$
上記の損失関数をTensorFlowのコードで次の様に表現します。
loss = tf.reduce_mean(tf.square(y - y_data))
- tf.reduce_mean() は引数に与えられた配列横断で、平均を求めます。[5]
- tf.square()は配列の各要素を2乗にします。[6]
勾配降下法の訓練モデルを設定
Wとbの値を最適化するために、損失関数の値を小さくなる様に徐々に調整していく、勾配降下法を指定します。 この時の学習率は 0.5 をおいています。 この値が小さいと計算に時間がかかり、大きいと発散するため、適切な値に調整する必要がある様です。 前述の損失関数(loss)をオプチマイザーに定義します。
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)
- tf.train.GradientDescentOptimizer() 勾配降下法を実装するオプチマイザー [7]
TensorFlowの初期化
TensorFlowのおまじない(定型的な手順)として、変数の初期化、セッションを開始して初期化します。
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
トレーニング
繰り返しオプチマイザを実行していくことで、勾配降下法によるWとbの最適値を求めていきます。 下記のコードでは、200回の最適化を実行して、10回毎に、Wとbの変化、関数の評価結果をプリントします。
for step in range(201):
if step % 10 == 0:
loss_val = sess.run(loss)
W_val = sess.run(W)
b_val = sess.run(b)
print('Step: %03d, Loss: %5.4f, W: %f, b: %f' % (step,loss_val,W_val,b_val))
sess.run(train)
予測関数
最適化されたWとbの値を利用して、未知のxから、予測を実行する関数を実装します。
def predict(x):
return W_val * x + b_val
グラフの描画
matplotlib.pyplotで、前述の予測関数で結果をプロットして、トレーニングデータを重ねて表示します。
fig = plt.figure()
subplot = fig.add_subplot(1,1,1)
plt.scatter(x_data,y_data)
linex = np.linspace(0,1,2)
liney = predict(linex)
subplot.plot(linex,liney)
plt.show()
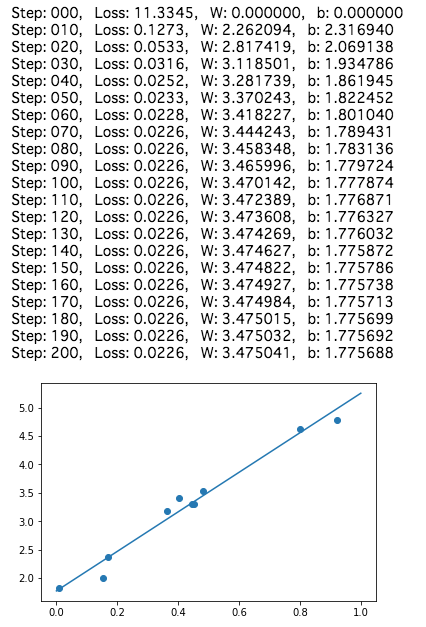
実行結果
Jupyter Notebookで実行して、Wとbを求めていきます。 90回程度のトレーニングで収束している様に見られます。
全リスト
以下は、jupyter notebookで 前述のトレーニング・データの作成の後続として実行することを想定したコードです。
import tensorflow as tf
# 最適化の対象の変数を初期化
W = tf.Variable(tf.zeros([1]))
b = tf.Variable(tf.zeros([1]))
# モデル
y = W * x_data + b
# 誤差関数
loss = tf.reduce_mean(tf.square(y - y_data))
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)
# 初期化
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
# トレーニング
for step in range(201):
if step % 10 == 0:
loss_val = sess.run(loss)
W_val = sess.run(W)
b_val = sess.run(b)
print('Step: %03d, Loss: %5.4f, W: %f, b: %f' % (step,loss_val,W_val,b_val))
sess.run(train)
# 予測関数
def predict(x):
return W_val * x + b_val
# グラフ描画
fig = plt.figure()
subplot = fig.add_subplot(1,1,1)
plt.scatter(x_data,y_data)
linex = np.linspace(0,1,2)
liney = predict(linex)
subplot.plot(linex,liney)
plt.show()
非線形回帰
線形回帰だけでは少し簡単すぎるので、多次元配列を利用した問題を解いてみるために、非線形回帰について取り組んでみます。
非線形回帰のトレーニングデータ作成
線形回帰のケースと同じ様に、Jupyter notebook を使って、乱数で xの配列データを作り、次の式で yの配列のデータを作ります。
$$ y = 0.14x^4 - 0.35x^3 + 0.2x^2 + 0.01x + 2 $$
同じ様に現実のデータっぽくするために、乱数を使って、yの配列データに乱数でノイズを加えておきます。
import numpy as np
import matplotlib.pyplot as plt
# データを生成
n=50
x_data = np.random.rand(n).astype(np.float32)
y_data = 0.14* x_data**4 - 0.35* x_data**3 + 0.2 * x_data*2 + 0.01*x_data + 2
# ノイズを加える
y_data = y_data + 0.009 * np.random.randn(n)
# ノイズ付きデータを描画
plt.scatter(x_data,y_data)
plt.show()
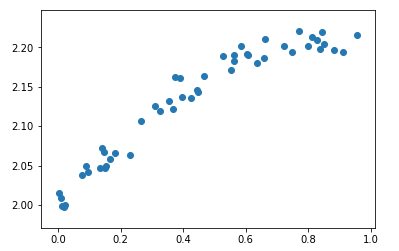
トレーニング・データの作成結果
次の図は、前述のコードで生成したトレーニング・データをプロットしたものです。
非線形回帰モデルと最適化対象のインスタンス化
非線形回帰のモデルとして、次の計算式を想定します。
y = w_0x^0 + w_1x^1 + w_2x^2 + w_3x^3 + w_4x^4
このモデルを多次元配列で表現すると、次の様に表すことができます。 ここで TensorFlow を使って w0,w1,w2,w3,w4 の最適値を求めていきます。
y_n=
\begin{pmatrix}
x_n^0 & x_n^1 & x_n^2 & x_n^3 & x_n^4
\end{pmatrix}
\begin{pmatrix}
w_{0} \\
w_{1} \\
w_{2} \\
w_{3} \\
w_{4} \\
\end{pmatrix}
この式を行列計算のモデルにします。
トレーニング・データの y0 〜 yn までを次の行列として表現できます。
y=
\begin{pmatrix}
y_{0} \\
y_{1} \\
\vdots \\
y_{n}
\end{pmatrix}
トレーニング・データのx0 〜 xn までを行列として次の様に表現できます。
X=
\begin{pmatrix}
x_{0}^0 & x_{0}^1 & x_{0}^2 & x_{0}^3 & x_{0}^4 \\
x_{1}^0 & x_{1}^1 & x_{1}^2 & x_{1}^3 & x_{1}^4 \\
\vdots & \vdots & \vdots & \vdots & \vdots\\
x_{n}^0 & x_{n}^1 & x_{n}^2 & x_{n}^3 & x_{n}^4 \\
\end{pmatrix}
求めるべき、wの行列です。
w=
\begin{pmatrix}
w_{0} \\
w_{1} \\
w_{2} \\
w_{3} \\
w_{4}
\end{pmatrix}
これでモデルは、行列計算として次の様に表現できます。
y = X w
この行列計算をTensorFlowのコードで表現すると、次の様になります。
xt = tf.placeholder(tf.float32, [None,5])
yt = tf.placeholder(tf.float32, [None,1])
w = tf.Variable(tf.zeros([5,1]))
y = tf.matmul(xt,w)
- tf.placeholder()は、トレーニング・データセットが格納される入れ物で、型と行列の情報を与えて空の状態で作ります。[9]
- tf.Variable() 最適化する対象となる変数です。 w0〜w1 まで5個の変数です。[10]
- tf.matmul() これは行列の内積を計算します。[11]
損失関数 (誤差関数)の定義
最適値を評価する損失関数は、訓練データと計算結果の差の合計を返します。
$$ E = \sum_{i=1}^{N} (y_{i} - yt_{i})^2 $$
この計算式をTensorFlowのコードで表現すると以下の様になります。
loss = tf.reduce_sum(tf.square(y-yt))
この損失関数を利用して、確率的勾配降下法を使って、w0,w1,w2,w3,w4 を求めていきます。
train = tf.train.AdamOptimizer().minimize(loss)
- tf.reduce_sum 行列横断で合計を計算します。 [12]
- tf.train.AdamOptimizer 確率的勾配降下法を実装したオプチマイザー [13]
トレーニングデータの準備
次の行列データを作成します。 縦がトレーニング・データ数になります。そして横が、非線形モデルの x にセットされる要素になります。
X=
\begin{pmatrix}
x_{0}^0 & x_{0}^1 & x_{0}^2 & x_{0}^3 & x_{0}^4 \\
x_{1}^0 & x_{1}^1 & x_{1}^2 & x_{1}^3 & x_{1}^4 \\
\vdots & \vdots & \vdots & \vdots & \vdots\\
x_{n}^0 & x_{n}^1 & x_{n}^2 & x_{n}^3 & x_{n}^4 \\
\end{pmatrix}
この式の配列を作るコードが以下になります。
x_train = np.zeros([n,5])
for i in range(0,n):
for j in range(0,5):
x_train[i][j] = x_data[i]**j
トレーニング
次のコードでトレーニングを実行します。 ここで、xt パラメータとして、トレーニング・データの x_train、 yt パラメータとして、y_train を train 関数へ渡していきます。
sess.run(train, feed_dict={xt:x_train,yt:y_train})
このトレーニングを12000回を繰り返しながら、1000回目づつで、損失関数の結果を表示するのが、次のコードです。
for step in range(12001):
if step % 1000 == 0:
loss_val = sess.run(loss, feed_dict={xt:x_train, yt:y_train})
print('Step: %03d, Loss: %5.4f' % (step,loss_val))
w_val = sess.run(w)
sess.run(train, feed_dict={xt:x_train,yt:y_train})
予測関数
TensorFlowで計算された w0〜w4 の最適値を使って、未知のxの計算結果を返す関数です。
def predict(x):
result = 0.0
for n in range(0,5):
result += w_val[n][0] * x**n
return result
描画処理
最後に、訓練データからTensorFlowで求めたパラメータを使ったモデルで計算した曲線を重ねてプロットします。
fig = plt.figure()
subplot = fig.add_subplot(1,1,1)
plt.scatter(x_data,y_data)
linex = np.linspace(0,1,100)
liney = predict(linex)
subplot.plot(linex,liney)
plt.show()
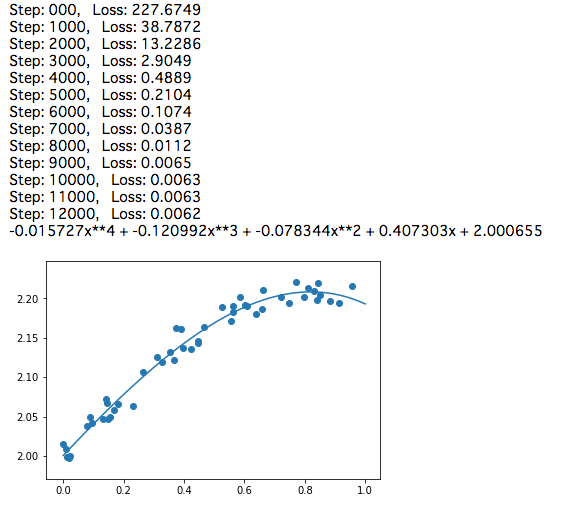
実行結果
Jupyter Notebookで実行した結果です。 元の式とはかなり違うw0,w1,w2,w3,w4の結果になりましたが、プロットしたグラフを見ると、適切な結果を出していることが理解できます。
全リスト
最初の訓練データを作るコードの続きとして、同じノートブック上で実行することを前提にしたコードです。
import tensorflow as tf
# モデル
xt = tf.placeholder(tf.float32, [None,5])
yt = tf.placeholder(tf.float32, [None,1])
w = tf.Variable(tf.zeros([5,1]))
y = tf.matmul(xt,w)
# 誤差関数
loss = tf.reduce_sum(tf.square(y-yt))
train = tf.train.AdamOptimizer().minimize(loss)
# TF初期化
sess = tf.Session()
sess.run(tf.global_variables_initializer())
# 先に作ったデータをトレーニング・データとして準備
y_train = y_data.reshape([n,1])
x_train = np.zeros([n,5])
for i in range(0,n):
for j in range(0,5):
x_train[i][j] = x_data[i]**j
# トレーニング
for step in range(12001):
if step % 1000 == 0:
loss_val = sess.run(loss, feed_dict={xt:x_train, yt:y_train})
print('Step: %03d, Loss: %5.4f' % (step,loss_val))
w_val = sess.run(w)
sess.run(train, feed_dict={xt:x_train,yt:y_train})
print('%fx**4 + %fx**3 + %fx**2 + %fx + %f' % (w_val[4],w_val[3],w_val[2],w_val[1],w_val[0]))
# 予測関数
def predict(x):
result = 0.0
for n in range(0,5):
result += w_val[n][0] * x**n
return result
# 描画
fig = plt.figure()
subplot = fig.add_subplot(1,1,1)
plt.scatter(x_data,y_data)
linex = np.linspace(0,1,100)
liney = predict(linex)
subplot.plot(linex,liney)
plt.show()
まとめ
TensorFlow を理解するために、参考資料の[1]、[2]を見ながら、独自に作った訓練データでトレーニングして結果を確かめました。 チュートリアルにあるプログラムの変形ですが、線形回帰 や 非線形回帰 のパラメータ決定にも簡単に適用できることが、コードレベルで理解できたので、とても価値があったと思います。 これから、もっと高度な問題にもチャレンジして、さらに理解を深めていきたいと思います。
参考資料
[1] TensorFlow, Getting Staeted r0.12, Indroduction https://www.tensorflow.org/versions/r0.12/get_started/
[2] TensorFlowで学ぶディープラーニング入門 ~畳み込みニューラルネットワーク徹底解説~ 中井 悦司
[3] docker docs, install Docker https://docs.docker.com/docker-for-mac/install/
[4] jupyter/tensorflow-notebook https://hub.docker.com/r/jupyter/tensorflow-notebook/
[5] tf.reduce_mean https://www.tensorflow.org/api_docs/python/tf/reduce_mean
[6] tf.square https://www.tensorflow.org/api_docs/python/tf/square
[7] tf.train.GradientDescentOptimizer https://www.tensorflow.org/api_docs/python/tf/train/GradientDescentOptimizer
[8] matplotlib.pyplot https://matplotlib.org/api/pyplot_api.html
[9] tf.placeholder() https://www.tensorflow.org/api_docs/python/tf/placeholder
[10] tf.Variable() https://www.tensorflow.org/api_docs/python/tf/Variable
[11] tf.matmul() https://www.tensorflow.org/api_docs/python/tf/matmul
[12] tf.reduce_sum() https://www.tensorflow.org/api_docs/python/tf/reduce_sum
[13] tf.train.AdamOptimizer() https://www.tensorflow.org/api_docs/python/tf/train/AdamOptimizer