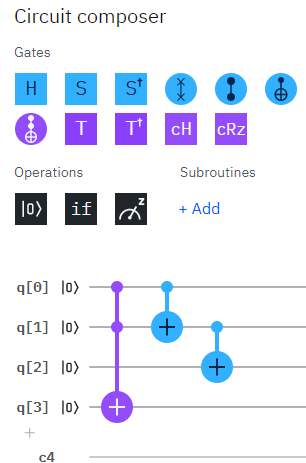
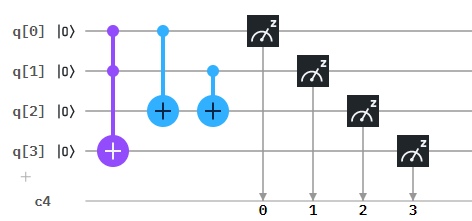
量子コンピュータ初心者です。前回に引き続き、IBM Quantum ExperienceとBlueqatを使って2進数の加算回路を作ってみます。
今回のゴール
今回は4量子ビットを用いて、2個の2進数を加算する計算機を作ってみたいと思います。最初は2量子ビットでなんとかならないかと思ったのですが妙案思い浮かばず、Blueqatの加算回路のチュートリアルを見ながら作ってみます。
2個の2進数の加算ですのでパターンとしては4通りあります。
- 0+0 = 00
- 1+0 = 01
- 0+1 = 01
- 1+1 = 10 ←桁上り発生
上から3番目までは普通ですね。4番目の1+1は10進数だと2になりますが、2進数なので桁上りが発生します。ここが1つのポイントでしょうか。これを量子ビットで入力と出力の関係が以下の表のように表現できれば完成です。
| 入力1 q[0] | 入力2 q[1] | 出力1桁目 q[2] | 出力2桁目 q[3] |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
ちょっとややこしいのですが出力は先の計算式とは逆にq[3]が1桁目、q[4]が桁上りした2桁目の順番にしています。トリッキーなように見えますが、Circuit Composerだと量子ビットの並び順と結果の並び順が逆になるので、これで問題ありません。
どの量子ゲートを使うか検討する
この演算をどのように量子ゲートを使って実現するかを考えます。先の表を見ると次のようなパターンを見てとれます。
- **q[0]とq[1]が共に0ならば、q[2]もq[3]も0
- q[0]かq[1]のどちらかが1のときだけq[2]が1になるが、q[3]は0
- q[0]とq[1]が共に1ならばq[2]は0で、q[3]は1**
1は特にゲート操作が必要なさそうなので、とりあえず無視します。
3はとっつきやすそうです。前回で取り上げた$CCX$ゲート(トフォリゲート)を使ってq[0]とq[1]を制御ビットにq[3]をターゲットビットにすれば、q[0]とq[1]が共に1ならばq[3]は1は簡単に実現できそうです。
2はq[0]が1のときにq[2]を1にするだけであれば、前々回で取り上げた$CX$ゲートで行けそうです。
厄介なのがq[0]とq[1]が共に1ならばq[2]は0の部分です。実はこれは$CX$ゲートの2段重ねでいけます。q[0]が1のときにq[2]を1にして、その後でq[1]が1であればq[2]を反転させることで0になります。
実際に回路を作ってみる
以上のアイディアを元にCircuit Composerで回路を作ってみます。
今回は4量子ビットを使いますので、'q' register qubitsを4にセットします。
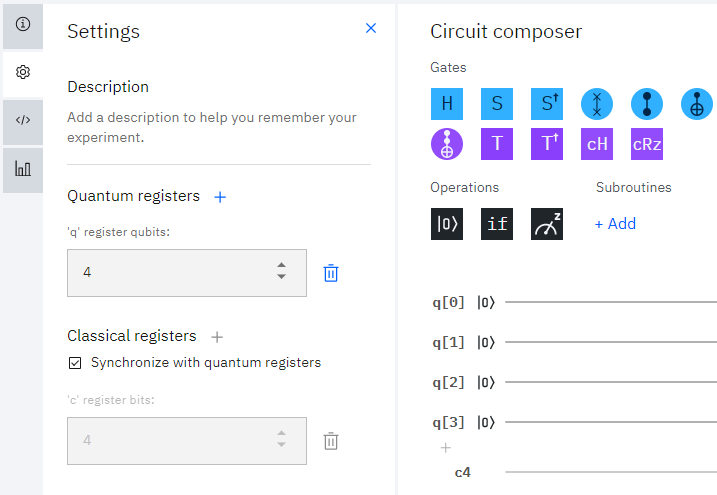
CCXゲートを追加する
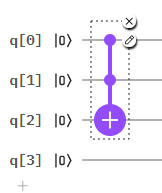
最初に$CCX$ゲートを追加します。普通にアイコンを置くとq[0]~q[2]にゲートが設置されました。が、ゲートを設置したいのはq[0],q[1],q[3]なのでこのままだと困ります。
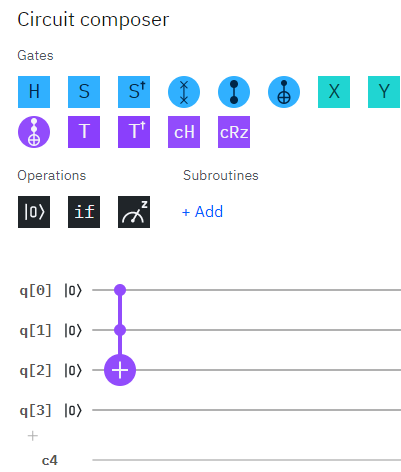
このような場合は設置したゲートを編集しましょう。ゲートをクリックして鉛筆マークの小さなアイコンをクリックします。
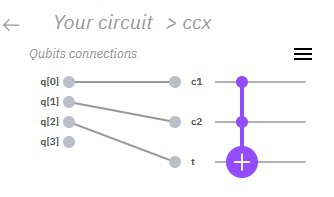
するとこのような画面に遷移します。
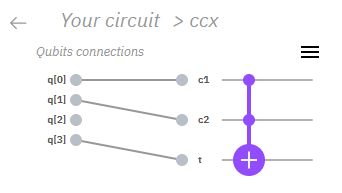
q[2]の結節点をドラッグ&ドロップしてq[3]につなぎ替えます。
元の画面に戻ると、無事ターゲットビットがq[3]に移動しました!
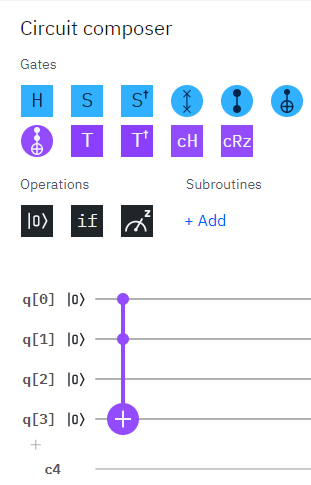
CXゲートを追加する
最初の$CX$ゲートはターゲットビットをq[2]にしたいので、先の要領で繋ぎ変えておきます。
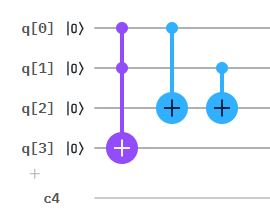
実際に計算してみる
結果(Measurement Probability)を見てみましょう。
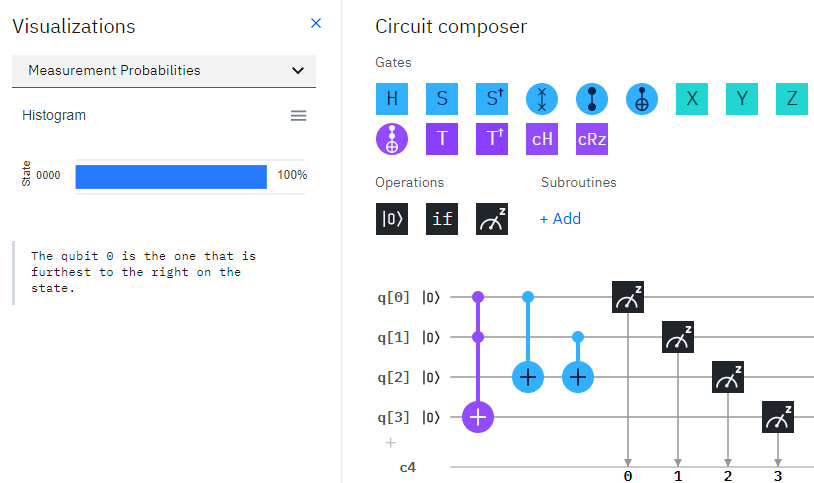
0+0
現在の状態はq[0],q[1]は共にゼロですので、結果も予想通り00となります。Circuit Composerではビットの順番と結果の並び順が逆ですのでq[3],q[2],q[1],q[0]の順で4桁で結果が出ていることに注意してください。
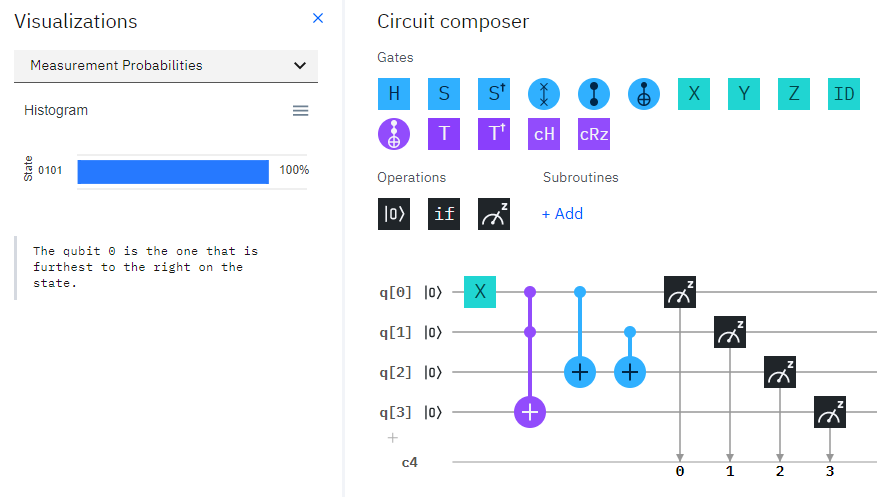
1+0
q[0]に$X$ゲートを入れて1にすると、結果は01(q[3]が1でq[4]が0)となります。
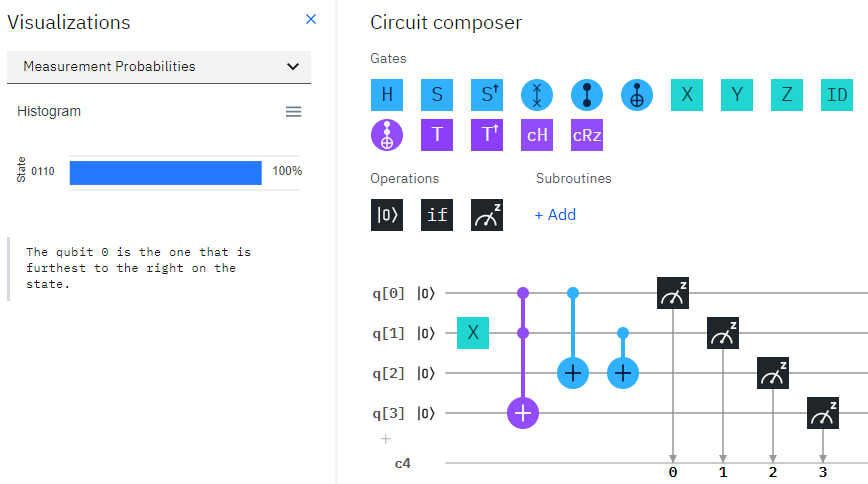
0+1
q[1]に$X$ゲートを入れて1にすると、結果は01(q[3]が1でq[4]が0)で同じですが、入力ビットの値(後ろ2桁)が01から10に変わっています。
1+1
q[0]とq[1]に$X$ゲートを入れて共に1にすると、結果は10(q[3]が0でq[4]が1)となります。
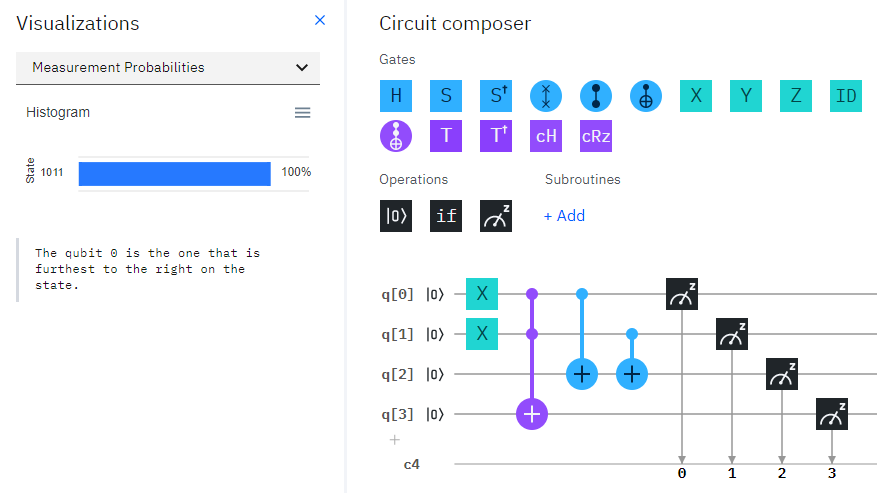
たった2つの加算ですが、無事回路が実現できました!
Blueqatで計算してみる
Blueqatでも計算してみます。チュートリアルのコードを少し改造して、まとめて4つの計算をできるようにしてます。
Blueqatではあらかじめadder=で作った回路を、Circuit().x[1] + adderのように別の回路に簡単に組み合わせができるのですね。。。とても便利です。サブルーチンを組むような感覚で使えそうです。
なお、前回までは説明の都合上Circuit(2)のように明示的に量子ビットの数を指定していましたが、BlueqatではCircuit()としても勝手に解釈してくれるようです。これもありがたい仕様ですね。
from blueqat import Circuit
res = []
adder = Circuit().ccx[0,1,3].cx[1,2].cx[0,2]
# 0+0
res.append((Circuit() + adder).m[:].run(shots=1))
# 0+1
res.append((Circuit().x[1] + adder).m[:].run(shots=1))
# 1+0
res.append((Circuit().x[0] + adder).m[:].run(shots=1))
# 1+1
res.append((Circuit().x[0].x[1] + adder).m[:].run(shots=1))
for i in res:
print(i)
実行結果です。Blueqatは量子ビットの順番通りに結果を出すので、Circuit Composerとは順番が逆の結果になります。
Counter({'0000': 1})
Counter({'0110': 1})
Counter({'1010': 1})
Counter({'1101': 1})