この記事は近畿大学 Advent Calendar 2019の21日目の記事です.
SOMってどんなもの?
SOMはニューラルネットワークの一種で与えられた入力情報の類似度をマップ上での距離で表現するモデルです.
と紹介されています.つまり入力データ(大抵は高次元データ)を低次元(大抵2次元)に写像することによって類似度をマップ上の距離で表現するニューラルネットワークです.SOMについてより詳しくしりたい方は先ほどのホームページで公開されているpdfをお読みください.
Somocluを使ってみる
SomocluとはSOMのライブラリです.なかなかSOMのライブラリがない中でしっかりしたライブラリだと思います.
3次元データを表現する
公式ページにしたがって3次元データを分類分けしてみようと思います.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import somoclu
c1 = np . random . rand ( 50 , 3 ) / 5
c2 = ( 0.6 , 0.1 , 0.05 ) + np . random . rand ( 50 , 3 ) / 5
c3 = ( 0.4 , 0.1 , 0.7 ) + np . random . rand ( 50 , 3 ) / 5
data = np . float32 ( np . concatenate (( c1 , c2 , c3 )))
colors = [ "red" ] * 50
colors . extend ([ "green" ] * 50 )
colors . extend ([ "blue" ] * 50 )
fig = plt . figure ()
ax = Axes3D ( fig )
ax . scatter ( data [:, 0 ], data [:, 1 ], data [:, 2 ], c = colors )
labels = range ( 150 )
n_rows , n_columns = 100 , 160
som = somoclu . Somoclu ( n_columns , n_rows , compactsupport = False )
som . train ( data )
som . view_umatrix ( bestmatches = True , bestmatchcolors = colors , labels = labels )
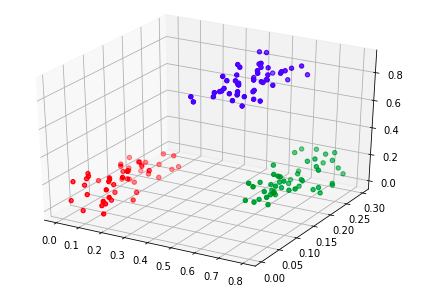
上記のコードで生成した3次元データがこちらで
学習後の画像はこちらです.
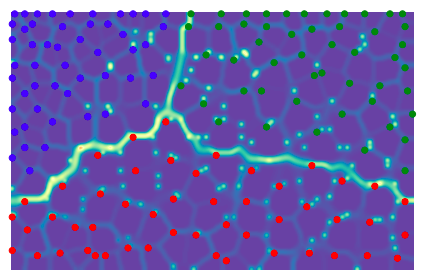
2次元空間に写像してもうまく似たデータ(3次元空間上で同じ郡に属していたもの)で固まっているのがわかると思います.
巡回セールスマン問題を解きたい!
そもそも巡回セールスマン問題とはなんでしょうか.[wiki]で調べてみると(https://ja.wikipedia.org/wiki/%E5%B7%A1%E5%9B%9E%E3%82%BB%E3%83%BC%E3%83%AB%E3%82%B9%E3%83%9E%E3%83%B3%E5%95%8F%E9%A1%8C)では
巡回セールスマン問題(じゅんかいセールスマンもんだい、英: traveling salesman problem、TSP)は、都市の集合と各2都市間の移動コスト(たとえば距離)が与えられたとき、全ての都市をちょうど一度ずつ巡り出発地に戻る巡回路のうちで総移動コストが最小のものを求める(セールスマンが所定の複数の都市を1回だけ巡回する場合の最短経路を求める)組合せ最適化問題である。
と紹介されています.巡回セールスマン問題は都市の数Nに対して計算量がO(N!)とNP困難な問題なので、通常近似解を求めていきます.
方針
今回はSOMの近い性質を持つものは潜在空間上の近い位置に写像される性質を利用して、1次元に写像するといい感じ(アホがバレる)に解が出てきそうだと考えました.
終わらなかった実装と他力本願な結末
はい、実装出来ませんでした.
ただ他の方が今年のアドカレでSOMで巡回セールスマン問題を解かれていたのを見ると1次元に写像する考えは間違って無さそう・・・.
最後に
流石にこのまま終わりたくないので自分で実装出来次第追記します.