この記事は古川研究室 Advent_calendar 13日目の記事です。
本記事は古川研究室の学生が学習の一環として書いたものです。内容が曖昧であったり表現が多少異なったりする場合があります。
はじめに
みなさん、こんにちは
みなさんは巡回セールスマン問題というものをご存知でしょうか。
まあよくある組み合わせ最適化問題の一種なのですが、本記事では私が巡回セールスマン問題を適当に解こうとした時の悲しい事件について書きたいと思います。
先に結論を言いますと丸め誤差って怖いねって話です。
プログラム初心者の頃の話なので全てにおいてハードルを低くして読んでいただけると幸いです。
巡回セールスマン問題
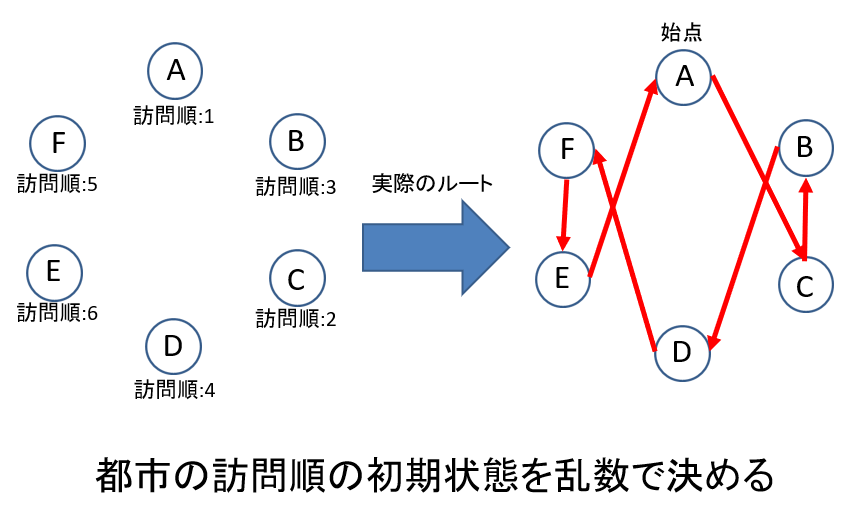
まず巡回セールスマン問題について説明したいと思います。巡回セールスマン問題とは「全ての都市を1度ずつ通って始点に帰る最短距離を求める問題」です。例えば次の図のように4つの都市A,B,C,Dが与えられると最短距離は次のようになります。
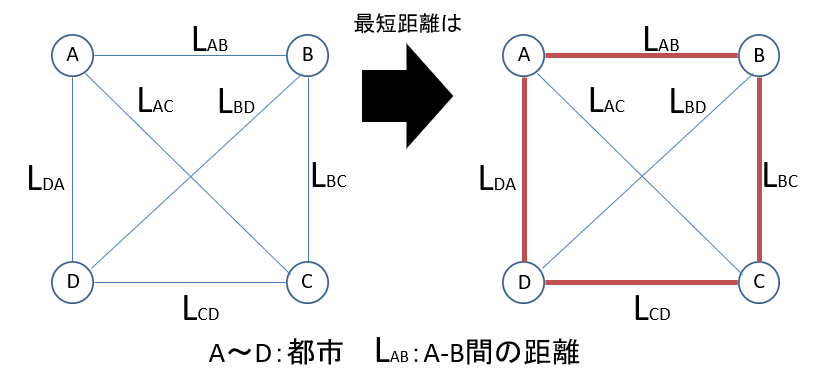
この場合は都市数も少なく、配置も簡単ですから見てすぐに最短距離が分かりますが、次の図のようにちょっと都市が増えると最短距離はぱっと見じゃわからなくなります。
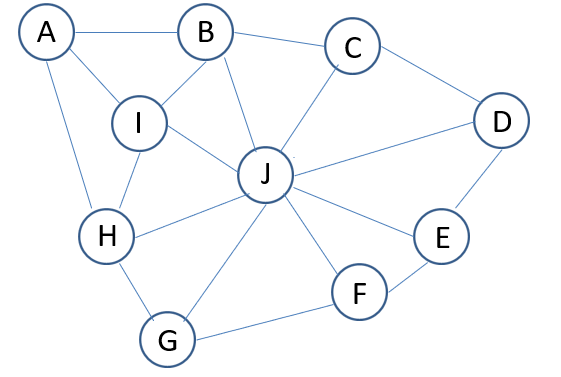
実は都市の訪問順の組み合わせ数は(都市の数-1)!となるので30都市、40都市となるとそれだけでえらい数の訪問順が存在することになり、とても全ての訪問順を調べるなんてことは難しくなるわけですね。
そこでこの組み合わせ最適化問題をそれなりにいい感じの解を得られるように適当に解いちゃおうとしたわけです。
SA法
組み合わせ最適化問題を解くうえで一番オーソドックスな汎用方法がSA法(Simulated-anearing)と呼ばれる方法です。日本語訳すると焼きなまし法となります。
焼きなまし法ではエネルギー関数$E$を設定します。今回の場合のエネルギー関数は全ての都市を回って始点に帰ってきた総合距離となります。この総合距離が下がるように都市の訪問順を入れ替えていきます。
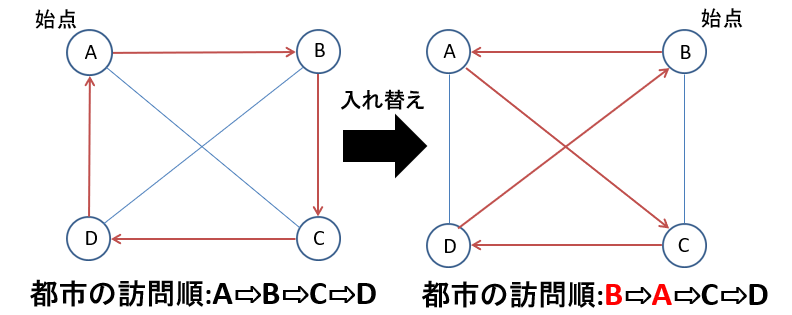
この場合だと総合距離は入れ替え前と比べて長くなってしまいます。なのでこの入れ替えを不採用としたいところですが、SA法では以下の式に示す確率でたとえ距離が長くなってしまっても入れ替えを採用します。
p=\exp \left\{-\frac{1}{T}\left(E_{t+1}-E_{t}\right)\right\}
ここで式中の$T$は温度と呼ばれるパラメータでノイズの役割をしています。$T$が大きいほど入れ替えを採用しやすくなります。また、入れ替えた結果距離が小さくなった場合は確率1で採用します。この方法をメトロポリス法と呼びます。
ここまでの流れをまとめると
- 訪問順を入れ替える
- メトロポリス法で入れ替えの採用不採用を決める
以降これを都市数分繰り返し1ステップとする
となります。
さらに、SA法では温度$T$をステップ数に合わせて以下の式で徐々に小さくしていきます。
T_{t+1}=\alpha T_{t}
また$\alpha$はどれだけ早く温度を下げるかの指標で$0<\alpha<1$の値を取ります。
この温度の下げ方をすることでステップ数の小さいときは入れ替えが発生しやすくなり、ステップ数の大きいとき、つまり終盤のときは入れ替えがあまり起こりにくくなるわけですね。
そうすると最初の方は局所解に陥っていても抜け出すことができますし、最後の方はきっちり決めてくれるような更新をしてくれるようになるわけです。
これは鍛冶の際に高い温度から始め徐々に冷やしていくことで鋼の強度を高めるところからきており、その由来で焼きなまし法と呼ばれています。
この方法は非常に組み合わせ最適化問題において強い汎用性があります。
アルゴリズムの反乱
さてここからが話したかったところです。私は上記の焼きなまし法を使って巡回セールスマン問題を解こうとしていました。アルゴリズム自体は簡単なのですぐに組めました。なのでめちゃめちゃ簡単な都市配置にしてテストしようとしたわけです。一番簡単な都市配置はおそらく円状です。
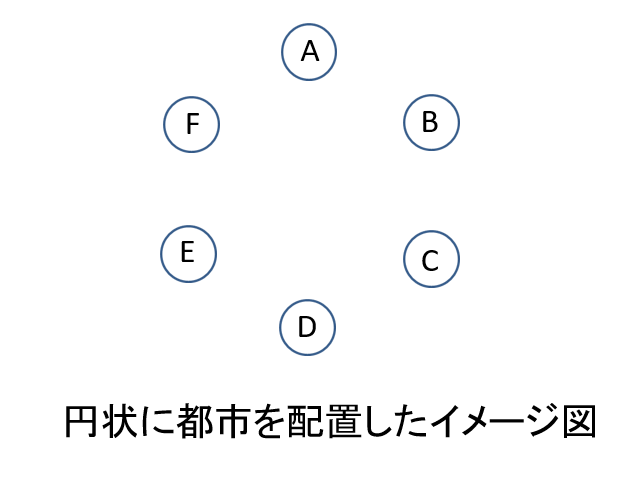
今回はこの都市配置を前提として話をしていきたいと思います。さて、おさらいですが焼きなまし法の手順は
一目で最短経路ではないとわかりますね。続いて入れ替える都市を決めましょう。ここも乱数で決めるのですが当時の僕はC言語を使っていたこともあり$0<x<1$の値を出力する一様分布に都市数$N$(int型)をかけることで$0<x<N-1$のint型乱数を生成していました。これが反乱の原因でした。
この自作した整数を出力する乱数を用いてシミュレーションを行いました。最初はステップ数100くらいだったのですが十分うまくいきます。600回入れ替えてるわけですからね。しかしある日事件は起こりました。ひょんなことから10000ステップ(60000回の入れ替え)試してみようと思い、シミュレーションを回したところ
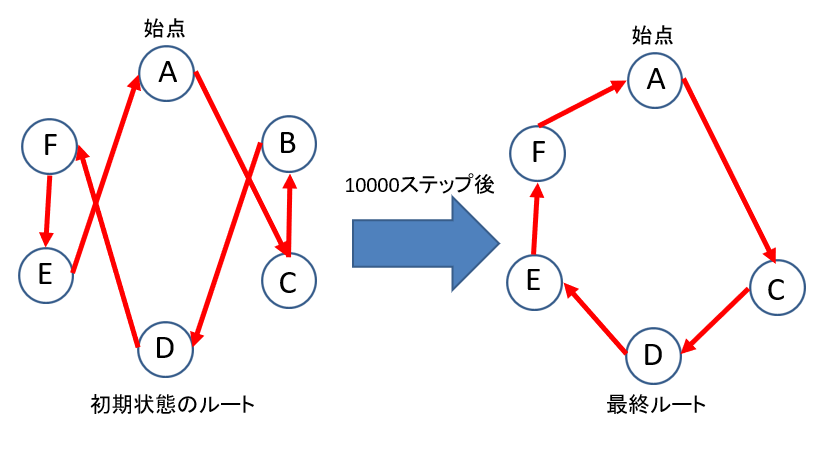
こんな結果が出ちゃいました。おかしいと思ったんです。座標を手計算した理論値を下回る総合距離が出力された時点で何かおかしいと思ってたんですよ。そりゃ当然ですよ、都市が消えちゃってるんですから。
しかもこの結果には再現性がなく1都市消えたり2都市消えたりなんなら消えなかったりとめちゃくちゃしてきます。プログラミングに慣れた人なら「再現性のない結果=乱数が悪さしている」とすぐピンとくるかもしれませんが当時の僕は駆け出しも駆け出し、頭を抱えてしまいました。
挙句の果てには「最短距離を出すためには都市が無くなればいいとアルゴリズムが判断したのでは?」と某スカイネットのような妄想すらしてしまいました。
オチ
もうお気づきの方もいらっしゃるとは思いますがオチとしては$0<x<1$の一様乱数を出す部分で極稀に丸め誤差のせいで1そのものが出力されちゃうことが原因でした。1が出力されちゃうとN番目の都市と入れ替えることになります。c言語の配列は0から数える決まりになっているので配列は0~N-1まで用意されていますから、N番目の配列は存在しません。そこから無を取得して入れ替えた結果、都市が消えちゃったんですね。
SOMと巡回セールスマン問題
またここから先は完全に別の話となってしまいますが、最近また巡回セールスマン問題に挑戦してみたのでそちらの結果を載せたいと思います。今回はSOMを用いて巡回セールスマン問題を解こうとしてみました。
SOMとはめちゃくちゃ簡単にいうと観測データ$\mathbf{Y}=(\mathbf{y}_1,\mathbf{y}_2,...\mathbf{y}_N)\in \mathbb{R}^{D×N}$と潜在変数
$\mathbf{X}=(\mathbf{x}_1,\mathbf{x}_2,...\mathbf{x}_K)\in \mathbb{R}^{M×K}$を繋ぐ滑らかな写像$\mathbf{f}:\mathbb{R}^{M}→\mathbb{R}^{D}$を推定することです
詳しいアルゴリズムについては我が研究室の教授が書いたドキュメントがあるのでそちらを参考にしていただけると幸いです。
例えば3次元のデータと2次元の潜在空間を与えるとこのような結果が生まれます。
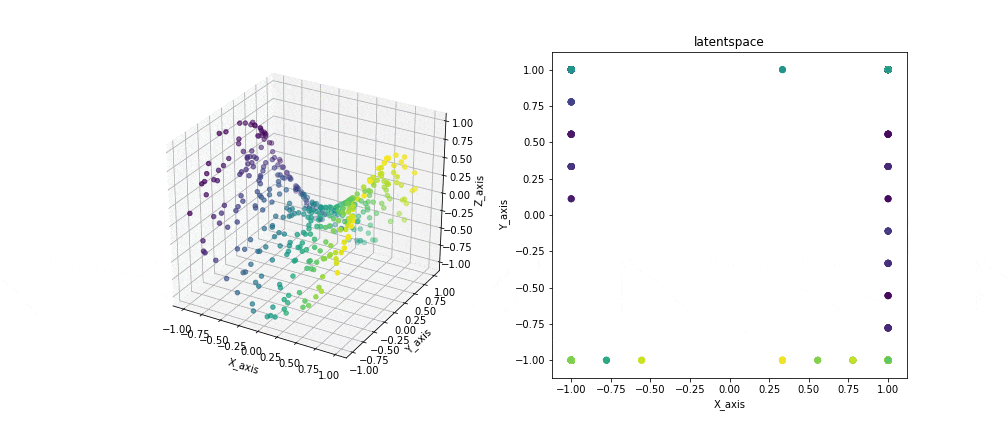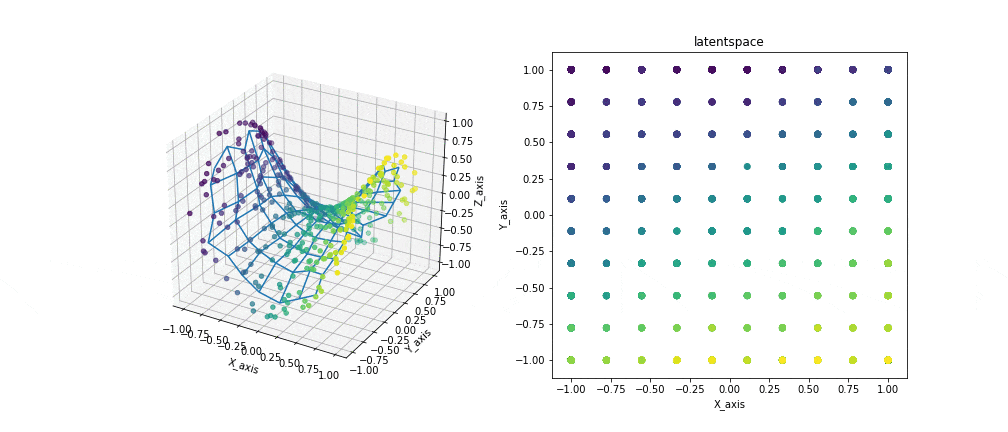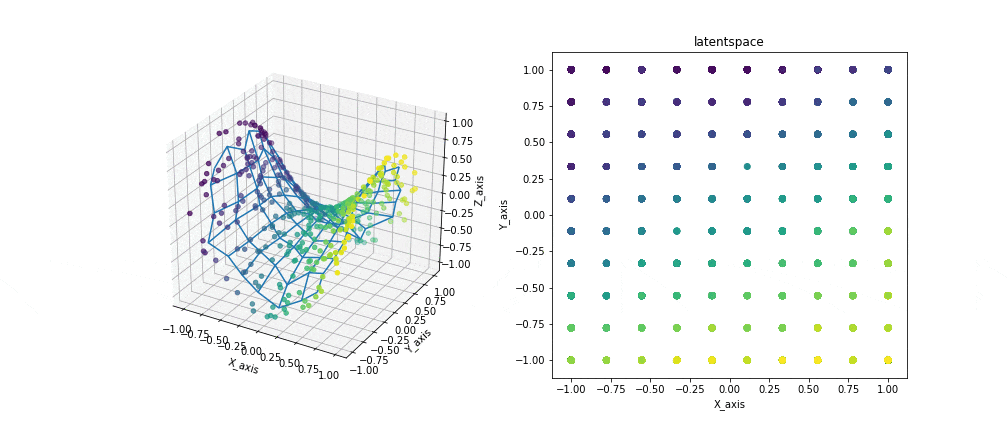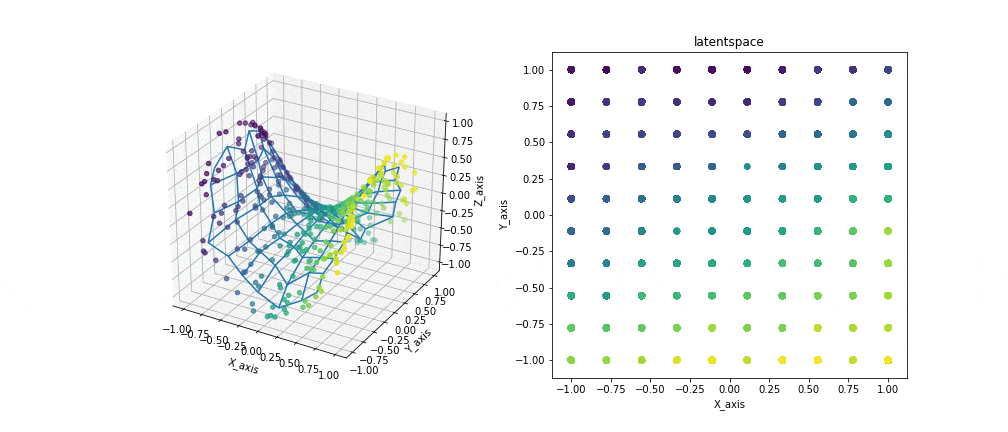
左の図では観測データと写像を、右の図では潜在空間を表示しています。
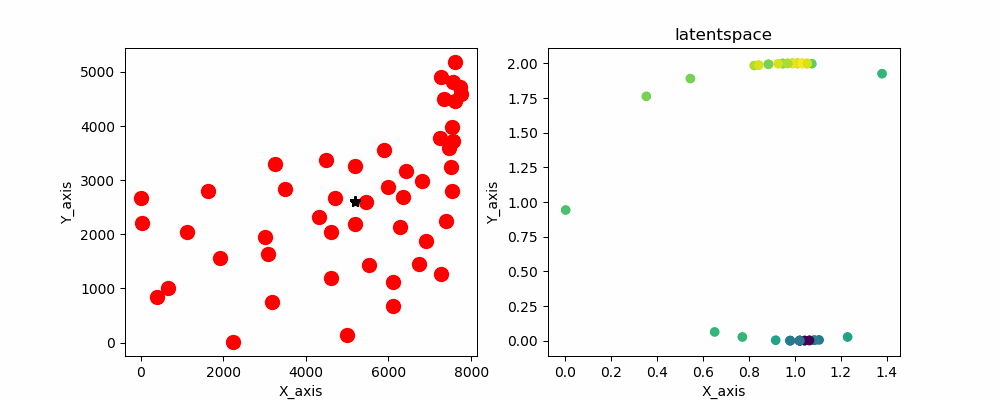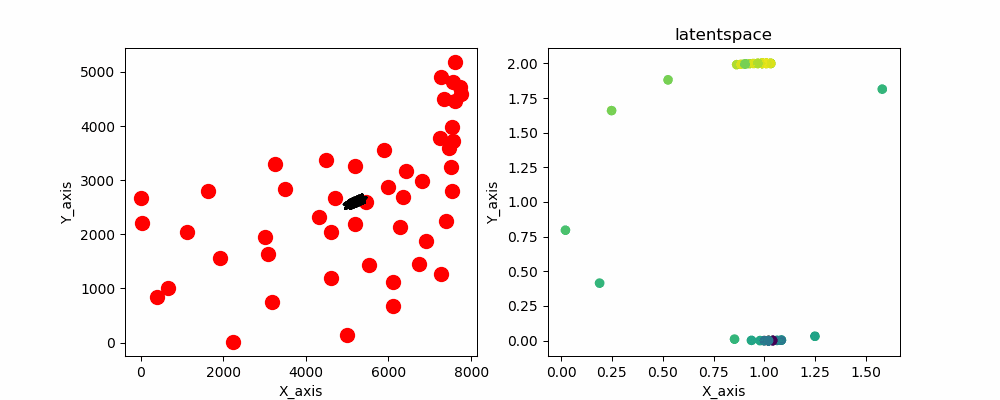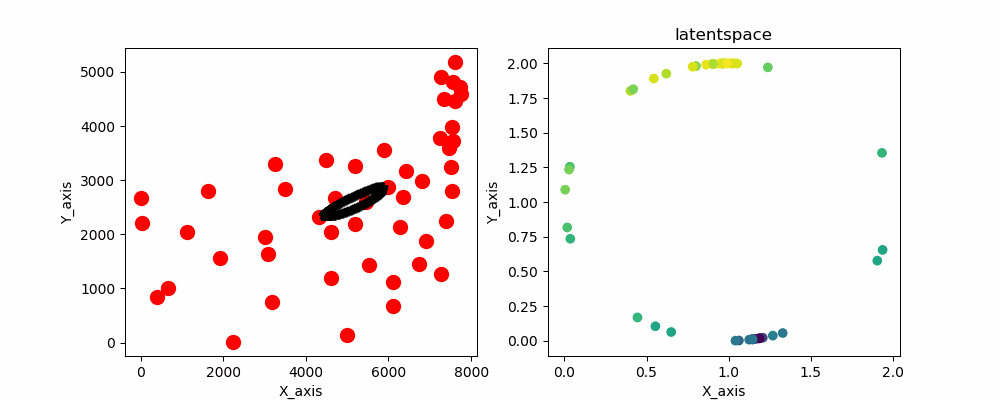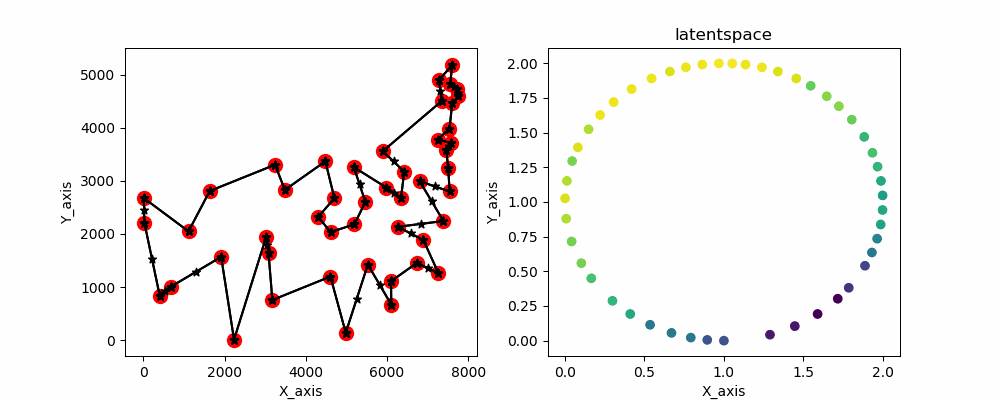
また、2次元のデータと1次元の潜在空間を与えるとこのような結果が生まれます。
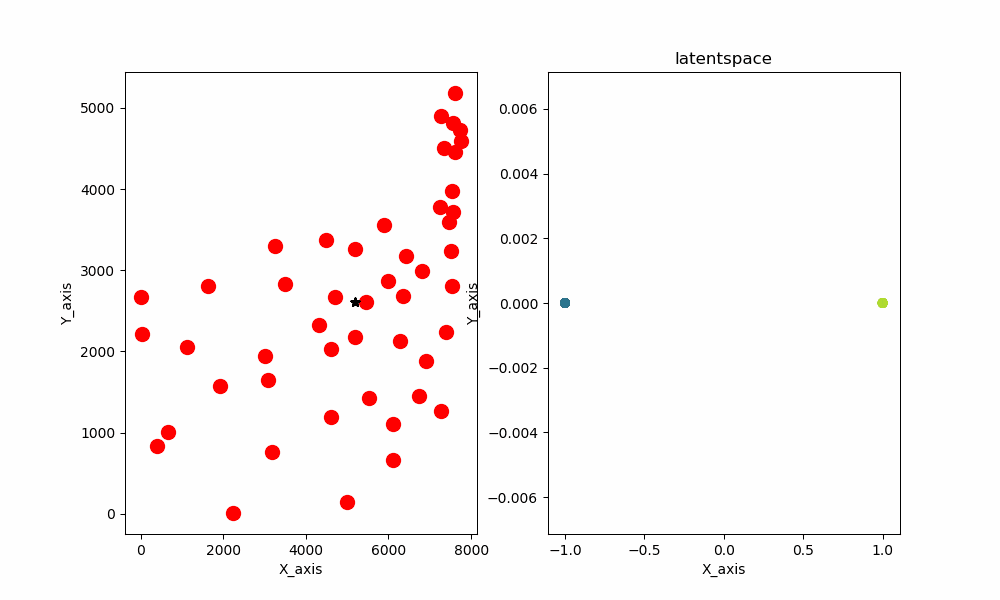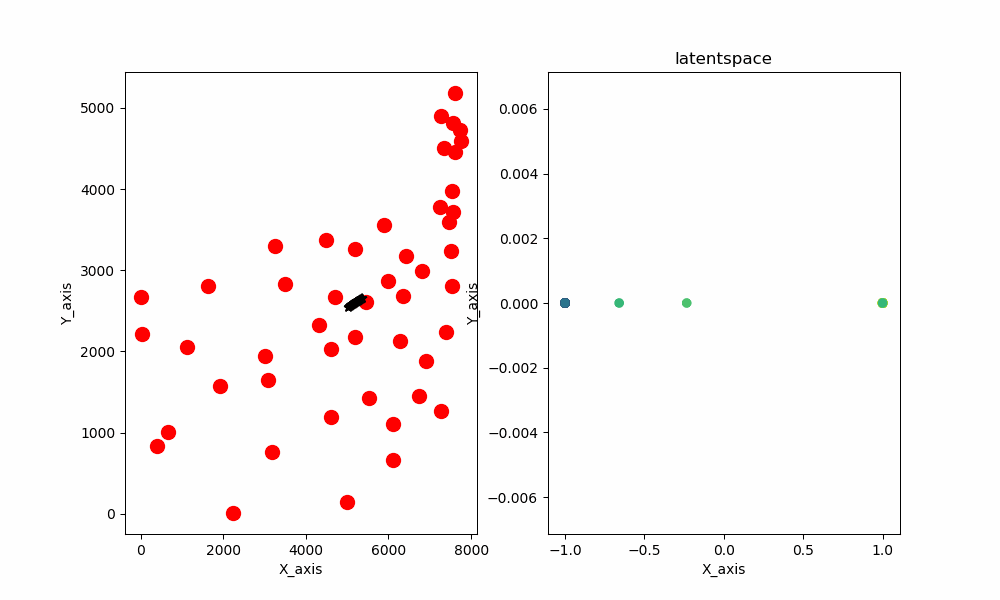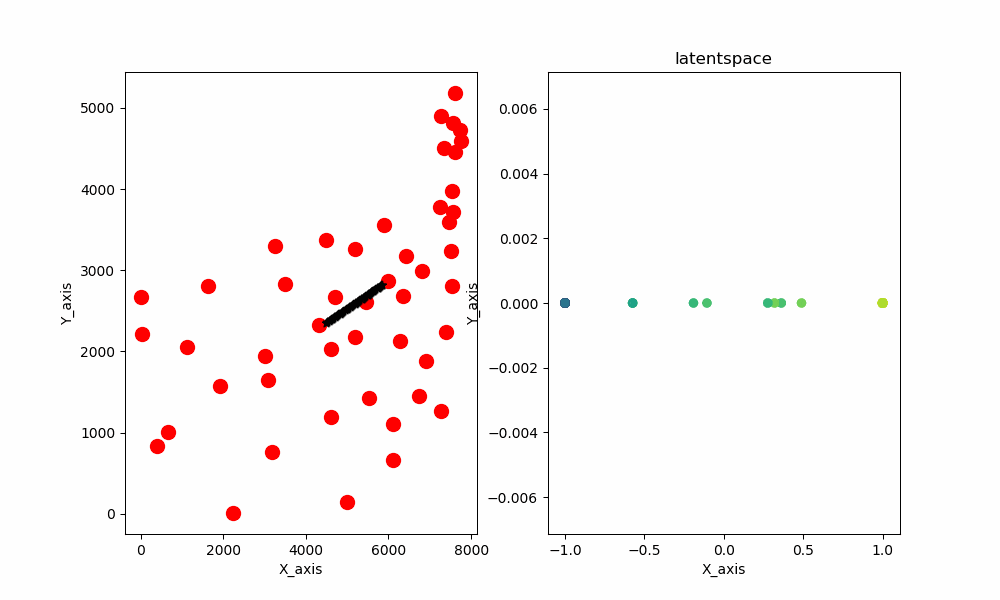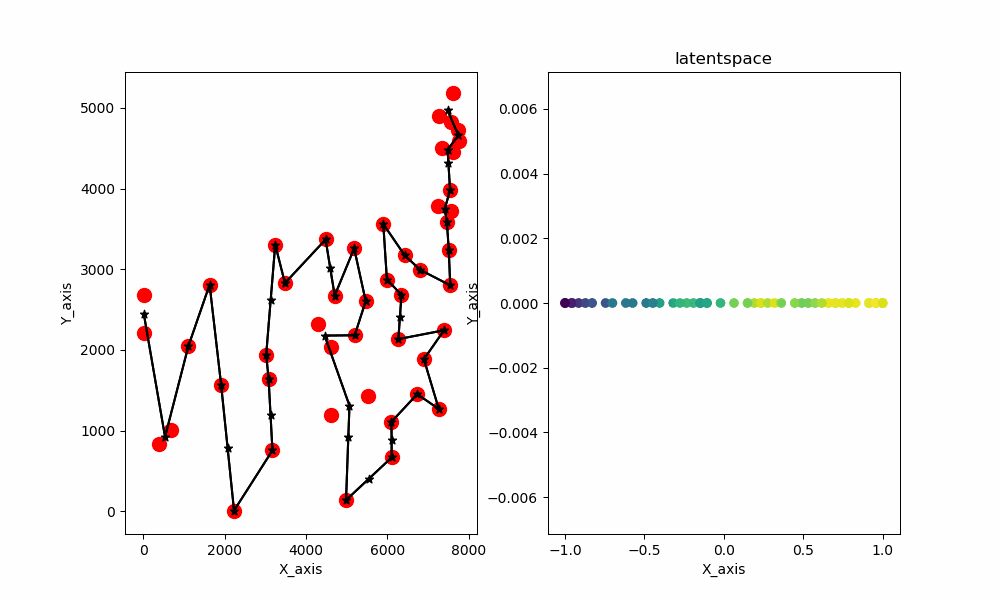
最終結果を示した画像はこちらとなります
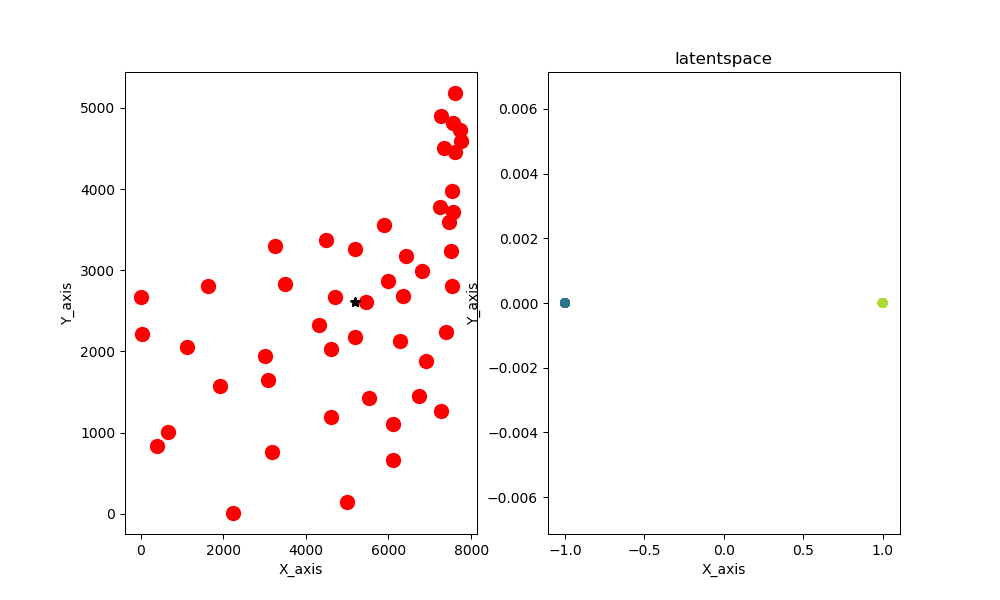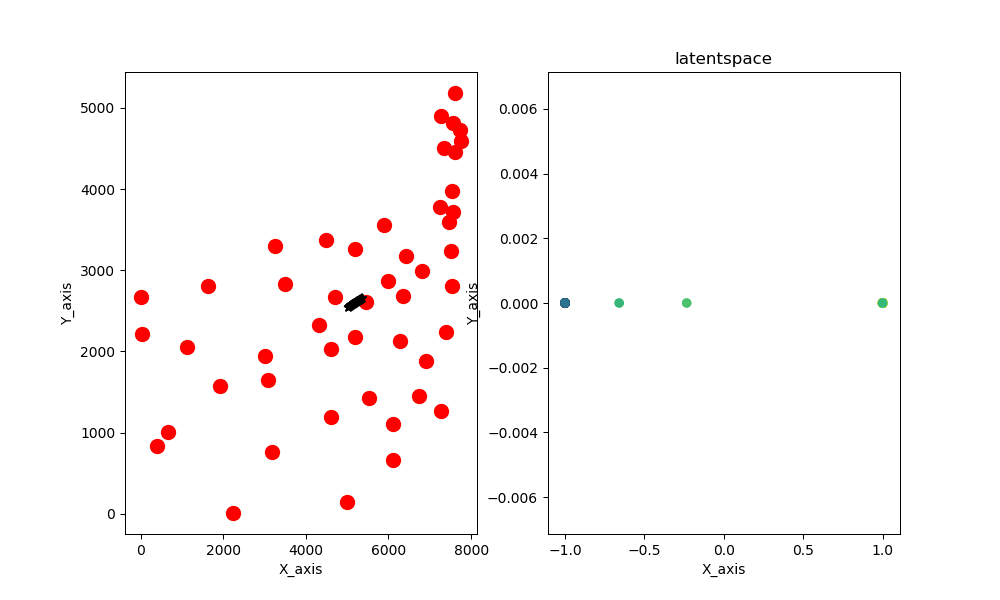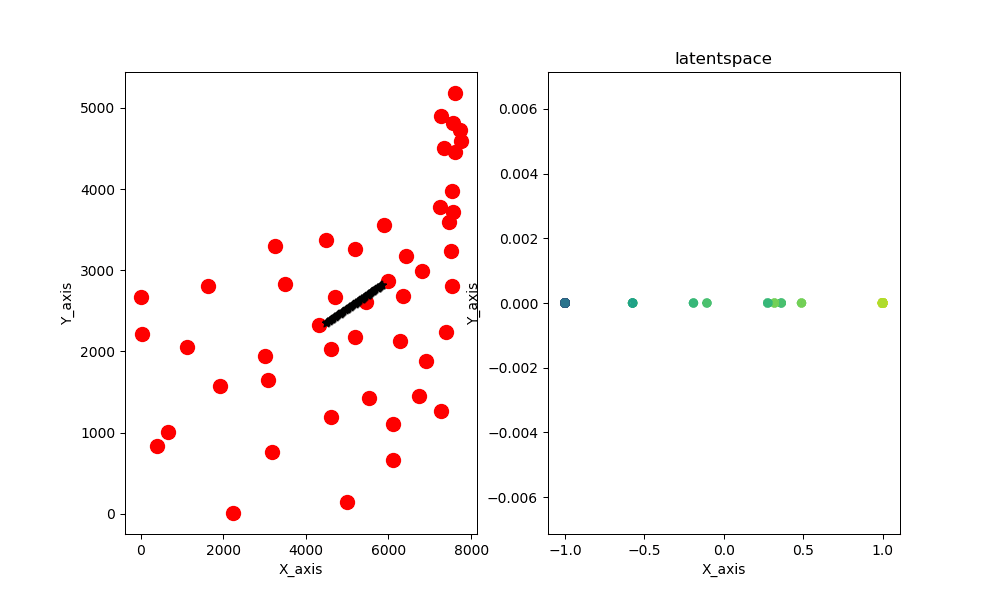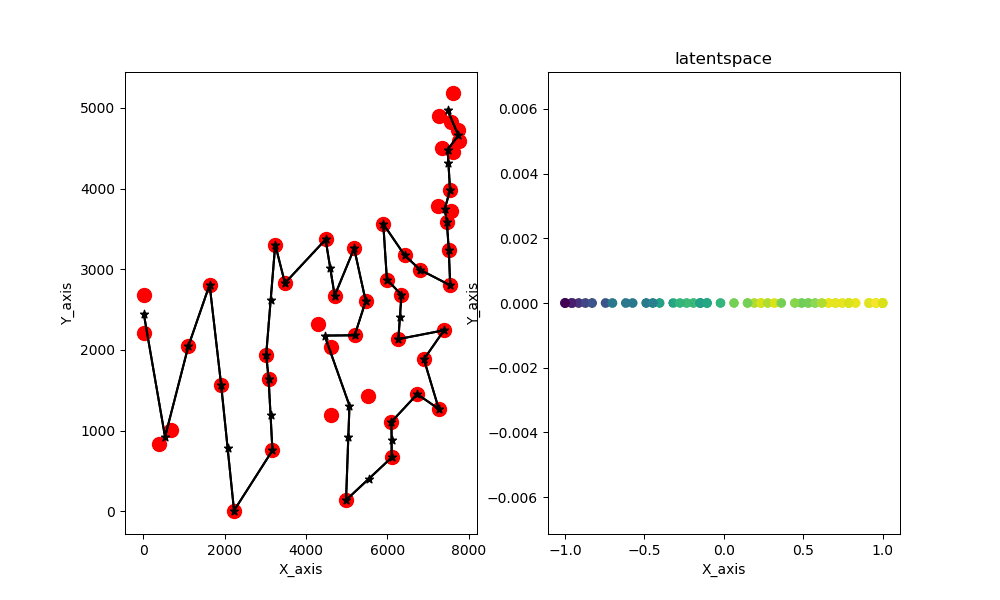
ちなみにデータとして与えているのはatt48と呼ばれるアメリカ48都市の座標データです。
なんか惜しいですよね。できそうな気がしてきます。
ここでネックなのは始点と終点が繋がっていないことです。それさえできれば終わりです。
なので始点と終点が繋がるような潜在変数を与えてあげます。そうです、潜在空間上に円状に潜在変数を配置します。
円状の潜在変数を配置したSOMのソースコードと実行結果がこちらとなります。
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
from numpy.random import*
import matplotlib.animation as anm
import math
import random
%matplotlib nbagg
fig = plt.figure(1,figsize=(6, 4))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
class som():
def __init__(self,N,K,sigmin,sigmax,r,w,zeta):
self.N = N
self.K = K
self.sigmin = sigmin
self.sigmax = sigmax
self.r = r
self.w = w
self.zeta = zeta
self.hist =[]
self.hist2 = []
self.hist3 = []
self.sigma=0
def fit(self,T):
for i in range(T):
#print(i)
if i==0 :
self.kn=np.random.randint(self.K,size=(self.N))
#if i%10 == 0 :
# self.sigma = self.sigma+0.5
self.sigma=max(self.sigmax-(i/self.r)*(self.sigmax-self.sigmin),self.sigmin)
#print(self.kn.shape)
self.test = (self.zeta[self.kn][None,:,:]-self.zeta[:,None,:])**2
#print("self,test=",self.test.shape)
#print("self,zeta=",self.zeta[self.kn][None,:,:].shape)
#print("self,zeta=",self.zeta[:,None,:].shape)
self.h_kn= np.exp(-1/(2*self.sigma**2)*np.sum((self.zeta[self.kn][None,:,:]-self.zeta[:,None,:])**2,axis=2))
#print(self.h_kn)
self.g_k = np.sum(self.h_kn,axis=1)
self.y_test =(1/(self.g_k[:,None]))*self.h_kn @ self.w
#print("y_test:{}",self.y_test.shape)
self.kn= np.argmin(np.sum((self.w[:,None,:]-self.y_test[None,:,:])**2,axis=2),axis=1)
self.X1=np.reshape(self.y_test,(K,2))
self.hist.append(self.X1)
self.hist2.append(self.kn)
self.hist3.append(self.sigma)
print(self.sigma)
print(np.array(self.hist).shape)
return self.hist,self.hist2,self.hist3
#self.hist.setdefault('y',[]).append(self.y_test)
#self.hist.setdefault('k',[]).append(self.kn)
#def history(self):
#return self.hist
a=0.1
c=-0.1
N=48#データ数
D=2#データの次元数
L=1#潜在空間の次元数
K=300#ノード数
T=100
zeta=np.zeros((K,2))
distance = 0
sigmax=5.0#sigmaの初期値
sigmin=0.01#sigmaの最小値
latent_space=np.random.normal
r=T-5#傾き
rad = np.linspace(-np.pi, np.pi, K)
zetax = np.sin(rad)+1
zetay = np.cos(rad)+1
zeta[:,0] = zetax
zeta[:,1] =zetay
train_data = np.loadtxt('att48.txt')
w = np.reshape(train_data,(48,D))
i=0
SOM = som(N,K,sigmin,sigmax,r,w,zeta)
kekka,k,sigma = SOM.fit(T)
kekka = np.array(kekka)
k = np.array(k)
sigma = np.array(sigma)
# print(k.shape)
for i in range(K):
#print(("x1",kekka[T-1,i,0]))
#print(("x2",kekka[T-1,i+1,0]))
#print(("y1",kekka[T-1,i,1]))
#print(("y2",kekka[T-1,i+1,1]))
#print(("x_delta",kekka[T-1,i,0]-kekka[T-1,i+1,0]))
#print(("y_delta",kekka[T-1,i,1]-kekka[T-1,i+1,1]))
if(i==K-1):
distance += np.sqrt(abs(kekka[T-1,i,0]-kekka[T-1,0,0])**2+abs(kekka[T-1,i,1]-kekka[T-1,0,1])**2)
else:
distance += np.sqrt(abs(kekka[T-1,i,0]-kekka[T-1,i+1,0])**2+abs(kekka[T-1,i,1]-kekka[T-1,i+1,1])**2)
#print("delta",np.sqrt(abs(kekka[T-1,i,0]-kekka[T-1,i+1,0])**2+abs(kekka[T-1,i,1]-kekka[T-1,i+1,1])**2))
print(distance)
# print(kekka.shape)
def update(i, zeta,w):
# for i in range(T):
print(i)
ax1.cla()
ax2.cla()
ax1.scatter(w[:,0],w[:,1],s=100,color='r')
ax1.scatter(kekka[i,:,0],kekka[i,:,1],color = 'k',marker = '*')
ax1.plot(kekka[i,:,0],kekka[i,:,1],color='k')
ax1.plot(kekka[i,:,0].T,kekka[i,:,1].T,color='k')
ax2.scatter(zeta[k[i,:]][:,0],zeta[k[i,:]][:,1],c=w[:,0])
ax1.set_xlabel("X_axis")
ax1.set_ylabel("Y_axis")
ax2.set_title('latentspace')
ax2.set_xlabel("X_axis")
ax2.set_ylabel("Y_axis")
ani = anm.FuncAnimation(fig, update, fargs = (zeta,w), interval = 100, frames = T-1,repeat = False)
ani.save("RSom_TSP_Node300.gif", writer = 'imagemagick')
gifだと一瞬で最終結果が消えちゃうので画像も用意してます。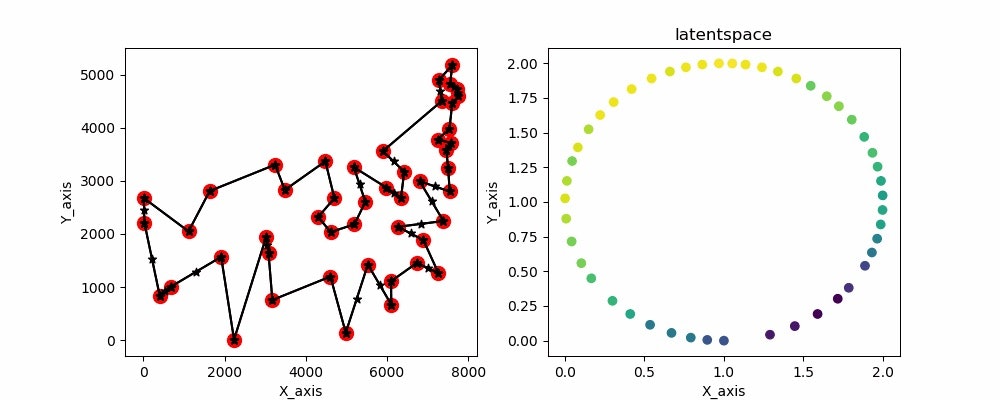
こちらです
めっちゃいい感じにできてますね 計算時間も早いのでかなりいい線いってると思います。あとはノイズとか加えて局所解を抜け出せるようにすればもっとよくなると思います。