やったこと
- 主成分分析(PCA)を行い、ホテリングT2統計量およびQ統計量を計算し、異常値の検出をやってみた。
- 部分二乗回帰分析(PLS)を行い、予測精度に対する前処理の影響などを比較してみた。
PCA
PCAについては他に優れた説明が溢れているので割愛。次元圧縮により膨大な変数の変動の大部分を少しの潜在変数で説明できるようになるのでとても便利。
ものづくりの現場では装置やセンサーからのたくさんの情報が得られるますが、1つずつ変動を追って異常に気づくことは難しいため、PCAで理解可能な次元まで落とし込んでモニタリングすることに利用されている。ただし、使用する潜在変数がどれだけもとの次元の情報を説明できているかに注意が必要。
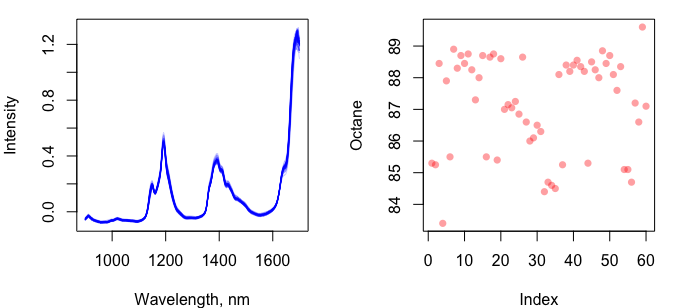
モデルデータとして、{pls}に含まれるgasolineデータを使用する。gasolineデータには、60個のガソリンの近赤外分光スペクトルデータとオクタン価のセットが含まれている。
60個のデータを7:3に分割し、7で主成分分析を行ってQ統計量やホテリングT2統計量のクライテリアを設定し、残りの3のデータの投影、異常値判定などを行った。
まずは、データの確認。
library(pls)
library(dplyr)
data(gasoline)
# wavelength of NIR spectrum
wl <- seq(900, 1700, 2)
# plot gasoline data
par(mfrow = c(1, 2), mar = c(4,4,1,2))
matplot(wl, t(gasoline$NIR), type = 'l', lty = 1, col = '#0000FF30',
xlab = 'Wavelength, nm', ylab = 'Intensity')
plot(gasoline$octane, col = '#FF000060', pch = 16, ylab = 'Octane')
次にデータの分割と主成分分析をした。
データは、60セットあるので、7割をtrain、残りの3割をtestにした。
主成分分析は、stats::prcomp()を用いて行った。分析結果の概要をsummary()で確認し、このデータセットにおいては2つの主成分で元のデータの分散のうち99.9%以上を説明できていることが確認できた。以降のtestデータの射影や異常値の検出は第2主成分までを使って行った。
# confirm dimension of NIR data
dim(gasoline$NIR)
# randam sampling
gr <- sample(1:60, 42) %>% .[order(.)]
# split data into train and test
train <- list()
train$x <- gasoline$NIR[gr,]
train$y <- gasoline$octane[gr]
test <- list()
test$x <- gasoline$NIR[-gr,]
test$y <- gasoline$octane[-gr]
# PCA model ----
PCAmodel <- prcomp(train$x, scale. = F, center = F)
summary(PCAmodel)
# Importance of components:
# PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8 PC9 PC10
# Standard deviation 5.8165 0.2096 0.06686 0.05798 0.04586 0.02740 0.02147 0.01750 0.01461 0.01288
# Proportion of Variance 0.9983 0.0013 0.00013 0.00010 0.00006 0.00002 0.00001 0.00001 0.00001 0.00000
# Cumulative Proportion 0.9983 0.9996 0.99977 0.99986 0.99993 0.99995 0.99996 0.99997 0.99998 0.99998
# continue ...
第2主成分までを使ってtestデータの主成分空間へ射影し、主成分スコアを取得する。predict()を使って射影を行うと返り値として主成分スコアが返される。
PCApred <- predict(PCAmodel, newdata = test$x)
head(PCApred[,1:2])
# PC1 PC2
# 5 -5.898345 0.173485951
# 10 -5.818701 0.145801384
# 12 -5.887769 0.145208816
# 16 -5.862742 0.003486377
# 18 -5.765301 0.082039319
# 25 -5.759995 -0.006302773
異常値検出
ここから、trainデータの主成分スコアとローディング(潜在変数に対する元の各特徴量の重み)からホテリングT2統計量およびQ統計量を求め、異常値検出のためのクライテリアを設定し、テストデータにおける異常値の確認を行った。
ホテリングT2統計量は、主成分スコアを標準化してから計算されたユークリッド距離に相当する。
ホテリングT2統計量のUCLは、第2主成分まで使用することを想定して算出した。
\alpha(x')=\sum_{i=1}^{M} \frac{(x'_{i} - \bar{\mu_{i}})^2}{\sigma_{i}^2}
サンプル数が多い場合、ホテリングT2統計量がカイ二乗分布に従うため、カイ二乗分布から有意水準$\alpha = 0.05$の場合の値を閾値とする。
# 各主成分の平均と分散
scoreMean <- apply(PCAmodel$x[,1:2], 2, mean)
scoreSD <- apply(PCAmodel$x[,1:2], 2, sd)
# T2統計量の算出
train$T2 <-
sweep(PCAmodel$x[,1:2], 2, scoreMean, FUN = '-') %>%
sweep(., 2, 2, FUN = '^') %>%
sweep(., 2, scoreSD ^ 2, FUN = '/') %>%
apply(., 1, sum)
test$T2 <-
sweep(PCApred[,1:2], 2, scoreMean, FUN = '-') %>%
sweep(., 2, 2, FUN = '^') %>%
sweep(., 2, scoreSD ^ 2, FUN = '/') %>%
apply(., 1, sum)
# UCLの算出
T2_UCL <- qchisq((1 - 0.05), 2)
# [1] 9.186547
Q統計量は、主成分スコアと負荷量(ローディング)から再構築されたデータと元のデータとの二乗誤差の総和をとったものである。
Q = \sum_{k=1}^{p} (x_k - \bar{x}_k) ^2
Q統計量の閾値は、トレーニングデータにおけるQ統計量の95パーセンタイルの値とした。
# Q統計量の算出
train$rev <- PCAmodel$x[,1:2] %*% t(PCAmodel$rotation[,1:2])
train$Q <- rowSums((train$x - train$rev) ^ 2)
test$rev <- PCApred[,1:2] %*% t(PCAmodel$rotation[,1:2])
test$Q <- rowSums((test$x - test$rev) ^ 2)
# QのUCLの算出
Q_UCL <- quantile(train$Q, c(0.95))
# 95%
# 0.02910094
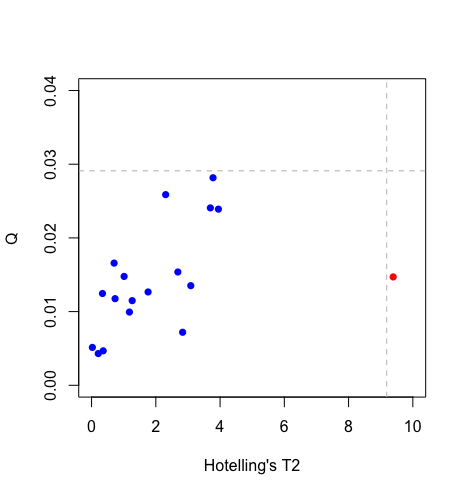
テストデータのホテリングT2統計量およびQ統計量、そしてそれぞれの閾値が求められたので、プロットとして異常値がないか確認してみた。
結果より、T2統計量において1つのデータが閾値を超えていることがわかった。以降のPLS分析にはこのデータを排除したものをテストデータとして使用することにした。
PLS
部分二乗回帰分析はplsパッケージのplsr()関数を用いて行う。潜在変数(factor)の数はncomp引数で10にし、バリデーションの方法はLeave-One-Outを指定した。
モデルの概要は、summary()関数でみることができる。潜在変数が7まではクロスバリデーションのRMSEP(平方平均二乗予測誤差)は減少し、その後増加しているため、潜在変数を8個以上にするとオーバーフィッティングの可能性が高くなると想定される。テストデータの予測の際には潜在変数を7つ使用することにした。
PLSmodel <- plsr(train$y ~ train$x, ncomp = 10, validation = "LOO")
summary(PLSmodel)
# Data: X dimension: 42 401
# Y dimension: 42 1
# Fit method: kernelpls
# Number of components considered: 10
#
# VALIDATION: RMSEP
# Cross-validated using 42 leave-one-out segments.
# (Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps 8 comps 9 comps
# CV 1.581 1.408 0.4536 0.2572 0.2402 0.2414 0.2193 0.2293 0.2351 0.2540
# adjCV 1.581 1.408 0.4500 0.2494 0.2428 0.2402 0.2183 0.2282 0.2339 0.2527
# 10 comps
# CV 0.2897
# adjCV 0.2875
#
# TRAINING: % variance explained
# 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps 8 comps 9 comps 10 comps
# X 70.68 80.56 84.68 95.13 96.31 97.13 97.76 98.40 98.80 98.97
# train$y 28.17 93.27 98.15 98.27 98.97 99.20 99.27 99.32 99.36 99.44
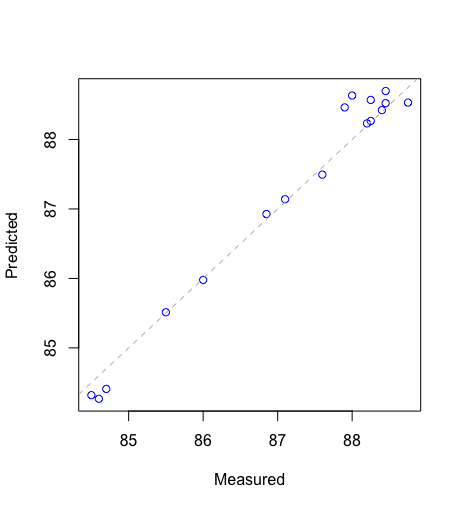
テストデータのオクタン価の予測結果を実測値に対してプロットした。RMSEは、0.264であった。
今回のデータは、ベースラインの変動などがあまりないデータであったが、そのような変動がある場合には、前処理としてSNV(Standard Normal Variate)処理やSavitzky-Golayの微分処理をするとより精度の高いモデルが構築できると思われる。SNV処理はbase::scale()、Savitzky-Golayの微分処理はsignal::sgolayfilt()を利用すると簡単に実行できる。