はじめに
医療統計や機械学習でよく使われるROC曲線ですが、機械学習を勉強するとROC曲線だけでなくPrecision-Recall曲線(PR曲線)というのもよく使われます。
どちらもAUCという面積を求めることで精度を比べるために使ったりします。
ROC曲線とPR曲線の違いを勉強していると以下の文章を見つけました。
Introduction to Data Science
ROC curves have one weakness and it is that neither of the measures plotted depend on prevalence. In cases in which prevalence matters, we may instead make a precision-recall plot. The idea is similar, but we instead plot precision against recall:
ROC曲線には1つの弱点があり、プロットされた測定値のどちらも有病率に依存しないということです。有病率が問題となる場合には、代わりに精密リコールプロットを作成することができます。考え方は似ていますが、代わりに再現率に対して精度をプロットします。(google翻訳)
@ogamikiさんのこちらの記事でも同じようなことが書かれていました。
TNの値が大きくなりやすい場合や、ネガティブケースが豊富な場合には、PR曲線が一般的に適しています。例えば、偏りが大きく、ポジティブケースが稀な場合にはPR曲線を使用します。一つの例として、不正検知の場合には、不正でないサンプルは10000あったとしても不正のサンプルは100以下という場合があります。ほかの場合にはROC曲線がより有用です。
具体例もあり読むと確かにそうなのですが、なぜネガティブケースが多い場合にそのようなことが起こるのかがよくわかりませんでした。
加えて予測の正確性にはaccuracyとprecisionがあり有病率がそれぞれにどのようにが影響を与えるのか気になります。
今回は混合行列を復習しながらRでプログラムを書いて考察してみたいと思います。
混合行列の復習
| 実際に病気だった | 実際には病気じゃなかった | |
|---|---|---|
| 検査で「陽性」と診断された | 真陽性(TP) | 偽陽性(FP) |
| 検査で「陰性」と診断された | 偽陰性(FN) | 真陰性(TN) |
| 用語 | 別の呼び方 | 機械学習での呼ばれ方 | 意味 |
|---|---|---|---|
| 感度(Sensitivity) | TPR | 再現率(recall) | 実際に病気だった人の中で陽性だった確率 |
| 特異度(Specificity) | TNR | 実際に病気じゃなかった人で陰性だった確率 | |
| 正確度 | accuracy | 診断の正確性 | |
| 適合度・精度 | precision | 陽性と言われた人の正答率 |
混合行列を感度、特異度、有病率(p)、人数(n)で代入して表現してみます。
真陽性 = n*p*感度
偽陽性 = n*(1-p)*(1-特異度)
偽陰性 = n*p*(1-感度)
真陰性 = n*(1-p)*特異度
正確度 = p*感度+(1-p)*特異度 #(真陽性+真陰性)/n
適合度 = p*感度/(1-特異度+p*(感度+特異度-1)) #真陽性/(真陽性+偽陽性)
Rを使ってグラフ化してみる
ここからRで有病率を変えてそれぞれの値がどうかわるのか計算してみます。
1例として感度を0.9、特異度を0.8、人数を10000人としてみます。
library(tidyverse)
n <- 10000
感度 <- 0.9
特異度 <- 0.8
有病率 <- c(seq(0,0.1,length.out = 11),seq(0.2,0.8,length.out = 7),seq(0.9,1,length.out = 11))
a <- map_df(有病率,function(p){
list(有病率 = p,
病気の人の人数 = n*p,
病気でない人の人数 = n*(1-p),
真陽性 = n*p*感度,
偽陽性 = n*(1-p)*(1-特異度),
偽陰性 = n*p*(1-感度),
真陰性 = n*(1-p)*特異度,
正確度 = p*感度+(1-p)*特異度,
適合度 = p*感度/(1-特異度+p*(感度+特異度-1)))
})
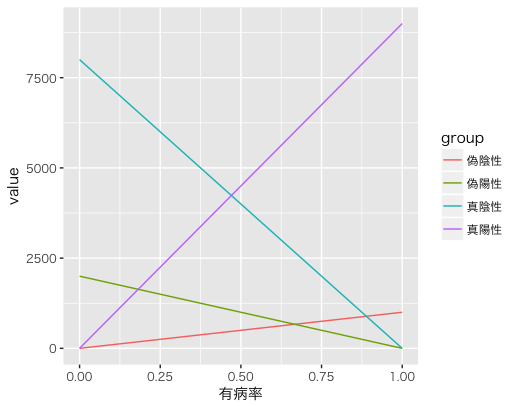
# 混合行列の値をグラフ化する
b<- a %>%
select(c(-病気の人の人数,-病気でない人の人数,-正確度,-適合度)) %>%
gather(key = "group", value, -有病率 )
b %>%
ggplot(aes(x=有病率,y=value, color=group))+
geom_line()+
theme_gray(base_family="HiraKakuPro-W3")
# 正確度と適合度をグラフ化する
c<- a %>%
select(c(-病気の人の人数,-病気でない人の人数,-真陽性,-偽陽性,-偽陰性,-真陰性)) %>%
gather(key = "group", value, -有病率 )
c %>%
ggplot(aes(x=有病率,y=value, color=group))+
geom_line()+
theme_gray(base_family="HiraKakuPro-W3")
結果
表
グラフ
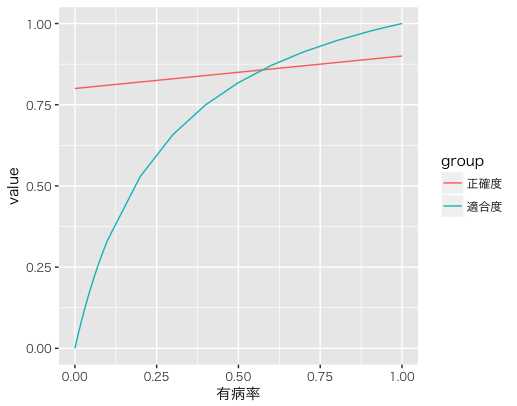
正確度(accuracy)は線形ですが、適合度(Precision)が反比例のようなグラフになっていて、確かに有病率が下がると正確度と適合度の乖離が広がることが見てとれます。
考察
混合行列から正確度と適合度を考える
このグラフを見ると、有病率が下がる(横軸の左側)に連れて「そもそも病気の人(真陽性+偽陰性)」が減り、「そもそも病気じゃない人(偽陽性+真陰性)」がかなり増えています。
上のグラフから一部抜粋
| 有病率 | 真陽性 | 偽陽性 | 偽陰性 | 真陰性 | 正確度 | 適合度 |
|---|---|---|---|---|---|---|
| 50% | 4500 | 1000 | 500 | 4000 | 0.85 | 0.82 |
| 10% | 900 | 1800 | 100 | 7200 | 0.81 | 0.33 |
| 1% | 90 | 1980 | 10 | 7920 | 0.80 | 0.04 |
そのためどうしても真陽性の数に対して偽陽性の数がふえることが適合度の低下に繋がっていると思われます。
特に真陰性の数が増えています。
数式から正確度と適合度を考えてみる
適合度はp*感度/(1-特異度+p*(感度+特異度-1))でした。
もしpの値が0に近づくと、分子→0、分母→1-特異度となり限りなく0に近づきます。
そのため適合度はpの影響を受けると言えます。
それに比べ正確度はp*感度+(1-p)*特異度でした。
よく式を見ると、pが下がれば’p*感度’の値が減るかわり’(1-p)*特異度’の値が増え、pが増えるとその逆になっていることが見てとれます。
pが0だと正確度=特異度。しかも特異度が高ければ真陰性の値が増えるので、正確度は適合度ほど影響を受けないと思われます。
ROC曲線は?
ROC曲線は横軸に偽陽性、縦軸に感度を取ります。
感度は真陽性/(真陽性+偽陰性)=n*p*感度/(n*p*感度+n*p*(1-感度))=感度と数式からpが消え、pの影響を受けないことがわかります。
偽陽性は1-特異度=1-真陰性/(偽陽性+真陰性)=n*有病率*特異度/n*(1-p)*特異度/(n*(1-p)*特異度-n*(1-p)*特異度)=1-特異度となり、感度と同様にpの影響を受けないことがわかります。
縦軸も横軸もpの影響を受けないのでROC曲線のした面積であるAUC影響がありません。
PR曲線は?
PR曲線は横軸にrecall(感度)、縦軸にprecision(適合度)を取ります。
縦軸である適合度はこれまであったようにpの影響を受けpが下がると適合度が下がるので、面積であるAUCも下がることになります。
まとめ
今回は有病率がROC曲線とPR曲線のそれぞれにどのようにな影響を与えるのか検討してみました。
なぜ有病率が低い、もしくはネガティブケースが多い場合、accuracyやROCのと比べてprecisionやPR曲線を選ぶのか理解できました。