座標変換 回転行列 まとめ

はじめに

いろいろと座標変換を行う必要があったのでそのまとめです

github:https://github.com/Shunichi09/Qiita/tree/master/Functions
にも上がってます

目的

座標変換のメモ
https://physnotes.jp/mechanics/2d_rot_cor/
を参考にしています

表記

プログラムの表記と合わせています
thは$\theta$を
omeは$\omega$を意味してます

座標変換について

今は以下の状態を考えましょう
このような人($base$と表現します)が位置、角度、と速度、角速度を持っているとします

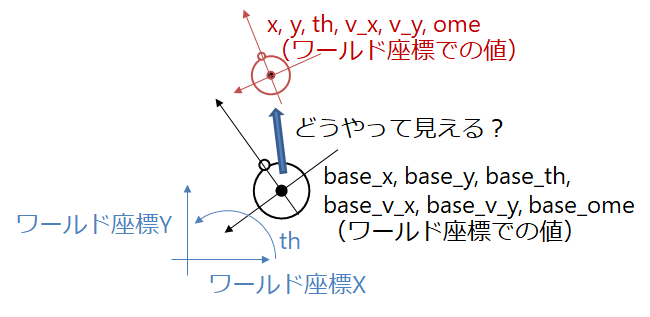
ではこの人からみた、違う人($X$と表現します)はどのように見えるかというのが座標変換です
つまり、今の人の状態がすべて0になり、そうなった場合の赤い人の状態を求めよという問題になります

この問題は平行移動と回転移動が共に存在するため少しややこしいです
手順としては以下の通り
まず以下の通り平行移動させます
これは単に引き算しているだけなので難しくはありません

\boldsymbol{X_{para}} = \boldsymbol{X}-\boldsymbol{X_{base}}

\boldsymbol{X} = 
\begin{bmatrix}
x & y & th & v_x & v_y & ome
\end{bmatrix}

\boldsymbol{X_{base}} = 
\begin{bmatrix}
x_{base} & y_{base} & th_{base} & v_{x_{base}} & v_{y_{base}} & ome_{base}
\end{bmatrix}

そして回転移動させます
これはいわゆる回転行列を使います
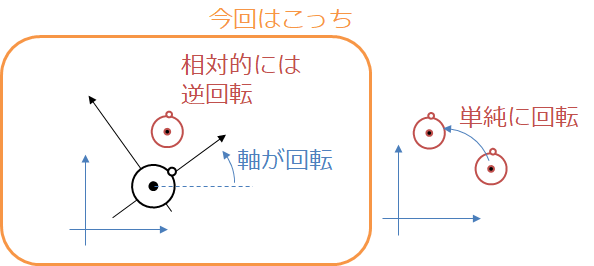
ただし、たまに勘違いしてしまいそうになりますがこれは、軸を回転させているということです
つまり，いつもの何度回転させてではなく，軸が回転しているので，相対的には逆回転していることになります
なのでいつも見慣れている行列とは逆に回転しているように見えるかもしれませんが，それは軸が回転しているからです

位置の軸の回転行列

\boldsymbol{X_{rot}} = 
\begin{bmatrix}
cos(th_{base}) & sin(th_{base}) \\
-sin(th_{base}) & cos(th_{base})
\end{bmatrix}
\begin{bmatrix}
x \\
y 
\end{bmatrix}

速度の回転行列

\boldsymbol{V_{rot}} = ome_{base}
\begin{bmatrix}
-sin(th_{base}) & cos(th_{base}) \\
-cos(th_{base}) & -sin(th_{base})
\end{bmatrix}
\begin{bmatrix}
x \\
y 
\end{bmatrix}
+
\begin{bmatrix}
cos(th_{base}) & sin(th_{base}) \\
-sin(th_{base}) & cos(th_{base})
\end{bmatrix}
\begin{bmatrix}
v_x \\
v_y 
\end{bmatrix}

すると求めることができます
こういう作業は機械学習なんかでのデータの事前処理に使えますね

もちろん戻せます
今度は回転移動⇨平行移動、さっきと逆の作業です
もちろん角度をマイナス、つまり逆回転、して代入しても同じにはなりますが、もともとの角度をそのまま使えた方がいいような気がしたのでこれで計算します
計算式は以下の通り

位置の回転行列

\boldsymbol{X_{rot}} = 
\begin{bmatrix}
cos(th_{base}) & -sin(th_{base}) \\
sin(th_{base}) & cos(th_{base})
\end{bmatrix}
\begin{bmatrix}
x \\
y 
\end{bmatrix}

速度の回転行列

\boldsymbol{V_{rot}} = ome_{base}
\begin{bmatrix}
-sin(th_{base}) & -cos(th_{base}) \\
cos(th_{base}) & -sin(th_{base})
\end{bmatrix}
\begin{bmatrix}
x_{rot} \\
y_{rot}
\end{bmatrix}
+
\begin{bmatrix}
cos(th_{base}) & -sin(th_{base}) \\
sin(th_{base}) & cos(th_{base})
\end{bmatrix}
\begin{bmatrix}
v_{x_{rot}} \\
v_{y_{rot}}
\end{bmatrix}

プログラムです
平行移動は単に引き算すれば良いので！
47行目まではそれぞれ位置の回転行列と速度の回転行列を作成するになります！
それ以降の関数は、その行列を作ってくれる関数を用いて平行移動と回転移動を全てやってくれる関数ですね

Rotation_and_parallele.py

import numpy as np
import math
import matplotlib.pyplot as plt

# thはラジアンです

# 回転行列の作成
# base_angle 何度回転させるか
def make_rot_mat(base_th):
    rot_matrix = [[np.cos(base_th), np.sin(base_th)], \
                  [-1*np.sin(base_th), np.cos(base_th)]]
    rot_matrix = np.array(rot_matrix)
    return rot_matrix

# 回転速度行列の作成
# 2つの行列を作成
def make_vel_rot_mat(base_th, base_ome):
    #第1項
    vel_rot_mat_1 = [[-1*np.sin(base_th), np.cos(base_th)], \
                     [-1*np.cos(base_th), -1*np.sin(base_th)]]
    vel_rot_mat_1 = base_ome * np.array(vel_rot_mat_1)
    #第2項
    vel_rot_mat_2 = [[np.cos(base_th), np.sin(base_th)], \
                     [-1*np.sin(base_th), np.cos(base_th)]]
    vel_rot_mat_2 = np.array(vel_rot_mat_2)

    return vel_rot_mat_1, vel_rot_mat_2

# 逆回転行列の作成
# baseはもともと回転させた角度
def make_inv_rot_mat(base_th):
    inv_rot_matrix = [[np.cos(base_th), -1 * np.sin(base_th)], \
                    [np.sin(base_th), np.cos(base_th)]]
    inv_rot_matrix = np.array(inv_rot_matrix)
    return inv_rot_matrix

# 逆回転速度行列の作成
# もとに戻す
def make_inv_vel_rot_mat(base_th, base_ome):
    #第1項
    inv_vel_rot_mat_1 = [[-1*np.sin(base_th), -1*np.cos(base_th)], \
                         [np.cos(base_th), -1*np.sin(base_th)]]
    inv_vel_rot_mat_1 = base_ome*np.array(inv_vel_rot_mat_1)
    #第2項
    inv_vel_rot_mat_2 = [[np.cos(base_th), -1*np.sin(base_th)], \
                         [np.sin(base_th), np.cos(base_th)]]
    inv_vel_rot_mat_2 = np.array(inv_vel_rot_mat_2)

    return inv_vel_rot_mat_1, inv_vel_rot_mat_2

def rotation_parallele(x, y, th, v_x, v_y, ome, base_x, base_y, base_th, base_v_x, base_v_y, base_ome):
    # ①下準備
    X = np.array([x, y, th, v_x, v_y, ome])
    base_X = np.array([base_x, base_y, base_th, base_v_x, base_v_y, base_ome])

    # 回転行列の作成
    rot_mat = make_rot_mat(base_th)
    vel_rot_mat_1, vel_rot_mat_2 = make_vel_rot_mat(base_th, base_ome)

    # ②平行移動
    para_X = X - base_X

    # ③回転移動
    rot_xy = np.dot(rot_mat, para_X[:2].reshape(2,1))
    rot_v_xy = np.dot(vel_rot_mat_1, para_X[:2].reshape(2,1)) + np.dot(vel_rot_mat_2, para_X[3:5].reshape(2,1))

    # 入れ直し
    para_rot_x, para_rot_y = rot_xy[0, 0], rot_xy[1, 0]
    para_rot_th = para_X[2]
    para_rot_v_x, para_rot_v_y = rot_v_xy[0, 0], rot_v_xy[1, 0]
    para_rot_ome = para_X[5]

    print('座標変換前：\n x　= {0} \n y = {1} \n th = {2} \n v_x = {3} \n v_y = {4} \n ome = {5}'\
            .format(x, y, th, v_x, v_y, ome))
    print('基準状態：\n x　= {0} \n y = {1} \n th = {2} \n v_x = {3} \n v_y = {4} \n ome = {5}'\
            .format(base_x, base_y, base_th, base_v_x, base_v_y, base_ome))
    print('座標変換後：\n x　= {0} \n y = {1} \n th = {2} \n v_x = {3} \n v_y = {4} \n ome = {5}'\
            .format(para_rot_x, para_rot_y, para_rot_th, para_rot_v_x, para_rot_v_y, para_rot_ome))

    return para_rot_x, para_rot_y, para_rot_th, para_rot_v_x, para_rot_v_y, para_rot_ome

if __name__ == '__main__':
    x, y, th = 1.0, 2.0, 0.5 # thはラジアンです
    v_x, v_y, ome = 0.5, 0.75, 0.5 # omeはrad/sです

    base_x, base_y, base_th = 1.3, 2.5, 0.5
    base_v_x, base_v_y, base_ome = 0.5, 0.75, 0.5

    rotation_parallele(x, y, th, v_x, v_y, ome, base_x, base_y, base_th, base_v_x, base_v_y, base_ome)

試しに入れて計算してみてください！！