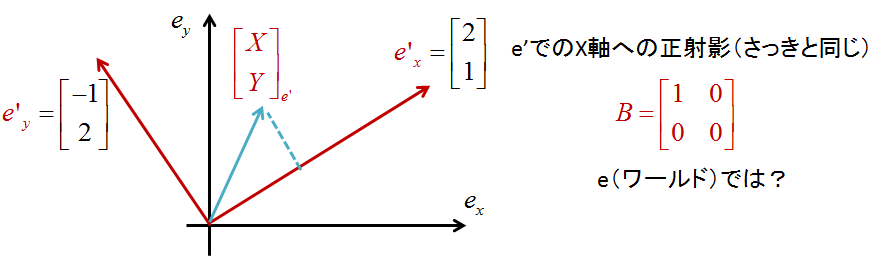はじめに
0から作るDeeplearning2が出版されてから,1か月がたとうとしています.
この夏にRNNと,経路計画,強化学習の基礎知識を一通り身に着けることを目標にしています!のでその一環です
全体的な感想としては僕がいうのもなんだとは思いますが,相変わらずの良書だと思います
変わらないとても高いクオリティーでRNNや自然言語処理の基本を理解することができました
心から購入をおすすめします
参考にした本
- ゼロから作るDeep Learning ❷ ―自然言語処理編 斎藤 康毅 オライリージャパン
- ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装 斎藤 康毅 オライリージャパン
オライリー社githubよりコピーしたものを張り付けています
参考github
- https://github.com/oreilly-japan/deep-learning-from-scratch-2
- https://github.com/oreilly-japan/deep-learning-from-scratch
今回のコメント付きプログラム
本記事の概要
各Chapter(本記事ではchapter4まで)を読んだ感想と,疑問に思い,調べた点をまとめました
プログラムについての自分なりの細かい解説は,githubの各chapでのプログラムをみていただけると嬉しいです
各プログラムに対してコメントしています
Chapter1(NNの復習)
概要
前回のDeeplearningの復習,前回の内容が分かっていればすらっと読める
追加されたところとしては
- 分岐ノードの説明
- Repeatノードの説明
- Sumノードの説明
- 計算の高速化(ビット精度の話)
- cupyの説明と実装方法
といったところ
プログラム
前回からのプログラムの変更として
Trainer Classが実装された
Trainer Classにはネットワークのモデルと,最適化勾配法に何を使うか(AdamやSGDの話)をいれる
で,fitするときに,入力データと教師データをいれればよくなった
trainer = Trainer(model, optimizer)
fit = Trainer(x, t)
また,今まで重みやレイヤーを
params = {}
params['W1'] = ...
layers = {}
layers['Affine1'] = Affine(params['W1'], params['b1'])
のように辞書型で扱っていたが今回からリストで扱う
layers = [layer1, layer2]
params = []
for layer in layers:
params += layer.params
なお,各layerクラスでは
[W]
で重みを処理している
なんでわざわざ[ ]で囲ってるのかと思ったが,ようは 上記のプログラムで配列の足し算する際に,
[[w1], [w2]]
のようにしたいからかなと
感想
前回の本もしっかり読み切っていたのと,pythonの知識が前回の本を読んだときよりもはるかに向上したので,すらすら読めた
そんなに難しくない
疑問点
さっきの[ ]で重みを処理しているところは気になったが,上記で述べたとおり
なので,なし!
ただ,少し分岐のところで疑問に思ったところがあったので以下を参考にした
- ニューラルネットワークの実装 ─深層学習フレームワークの構成と Chainer の設計思想─ 得居 誠也
Chaper2(自然言語処理の導入)
概要
自然言語処理の基礎知識と基本知識の説明
- シソーラス
- コーパス
などのキーワードの導入
ほとんどがカウントベース手法による自然言語処理の説明
流れはこんな感じ
- 分布仮説に基づき,分散表現を取得したい
- 共起行列や相互情報量,次元削減を用いて,ベクトル表記へ
- ベクトルの類似度を判定
プログラム
基本的なところが多いので,特に疑問点はない
ただ,初心者の自分としては
ptbのところで
os
でいろんなことを出来ることを知り感激した
疑問点
単語分散表現のベクトルを次元削減する際に使用する特異値分解!
これが一番の疑問点
いろいろ調べたので下にまとめる
特異値分解,固有値分解
そもそも固有値分解ってなにっていう話,それが分かれば後は拡張なんだろうなって思ったので
固有値分解でいろいろ調べてみる
このスライドがめちゃくちゃわかりやすかったので
https://www.slideshare.net/taketo1024/ss-48472383
参考にまとめた
引用が中心なので,スライドもぜひ見てほしい
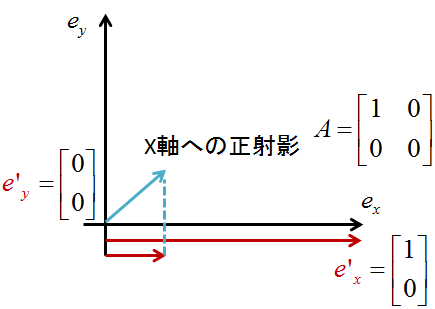
行列の掛け算の意味
スライドにもあるようにx軸への正写像を考えるとめっちゃわかりやすい
つまり,
\boldsymbol{Ax}\\
\boldsymbol{A} = \begin{bmatrix}
1 & 0 \\
0 & 0
\end{bmatrix} \\
というのは,なんと,
Aという基底空間での表現をワールド座標でみるとどういうことになりますか?
ことを表していることになる
もう少し詳しくいうと
たとえ,$x$のy成分が値をもっていたとしても,それは,ワールド座標には出てこない
ワールド座標っていうのは今まで使ってる
\boldsymbol{e_x} =
\begin{bmatrix}
1 \\
0
\end{bmatrix} \\
\boldsymbol{e_y} =
\begin{bmatrix}
0 \\
1
\end{bmatrix} \\
で表される空間
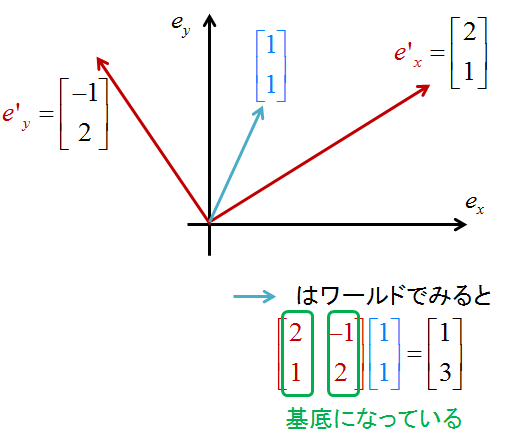
なので,下のイメージみたいな基底をとったときは
行列Aの成分を縦にみたときのベクトルがそれぞれの基底になっている
がそれぞれの基底を表していることになる
さてここで考えたいのはスライドにあるように異なる基底空間でのx軸への正射影
今異なる基底空間をさっきの図のように設定したとする
さて,ここでのx軸での正射影はどうなるのか?
その基底空間においてはx軸への正射影は簡単に表現できる(さっき述べたやつ)
でもこれは,その基底空間での話で,ワールドで見たらどうなるかわからない
なので,基底同士の変換を入れてしまえとなるわけ
それはさっきからいうように
行列の掛け算はある空間Uでのものをワールド座標でみたらってこと
逆の場合,つまりワールド座標での値をある空間にのせたらどうなりますかという話は,基底Uの逆行列で表現できる
なので
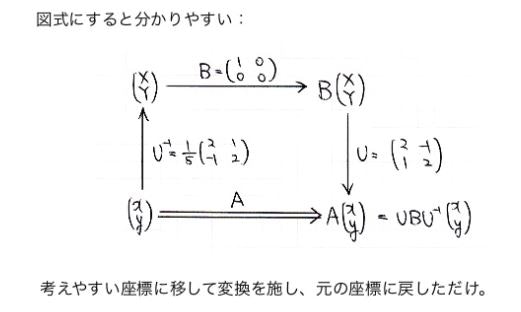
あとはこれを繋げればいい
イメージ図はこれ
スライドから引用しています
やりたいこと
さっきまでの流れを逆に使う
つまりある行列Aが与えられたときに
その行列を別の基底空間で表現するとどうなるの?
って話
でその時に!
行列Aをむちゃくちゃ簡単に表現できませんかね...
と考える
さっきのもAでみると複雑なのにある空間に飛ばすと簡単に表現できる
それをやりたい
ここで出てくるのが固有値と固有ベクトル
これを使えば,行列Aを簡単に表現できることになる
なぜなら,固有ベクトルはAという変換において大きさしか変わらないから
ってことは,固有ベクトルの空間に載せれば,行列Aは簡単に表現できるのでは?となる
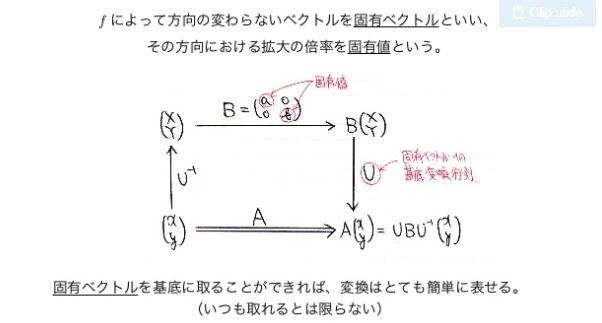
結論としては以下の図
以下もスライドから引用
つまり
さて,ここで固有値について考えてみる
この固有値で作られる行列Bは固有ベクトルの空間での変換を示しているわけだが
その時に固有値が小さいものというのは,ある基底空間においてその基底にかかる大きさが小さく,必要ないかも?ってことになる
なので,その成分は消してしまえばいいことになるってわけ
この考え方は特異値分解でも一緒
たぶん数学的な難易度は上がるけど,いけるはず(僕はここで止めときます)
納得!!
で結局
この削減によって次元の削減が行える
つまり,もとの行列Aを別の空間に飛ばしたときの基底で表現するってこと
Chapter3(word2vecの導入)
概要
推論ベースでの自然言語処理の考え方の導入
SVDが計算できなくなるカウントベースの手法の欠点をどう補っていくかという話から入り
NNでまず簡単なCROWモデルを作成し
予測ができそうなことを示す
また,skip-gramモデルも導入した
単純にCROWモデルが
入力:コンテキスト
出力:ターゲット
で予測器に,NNを使用していて,重みを単語の分散表現として使うってことが分かれば大丈夫な気がする
プログラム
おそらく一番悩むのが重みの共有の部分のプログラム
本では,説明は省略されているが,その部分だけ取り出すとこんな感じ
def remove_duplicate(params, grads):
'''
パラメータ配列中の重複する重みをひとつに集約し、
その重みに対応する勾配を加算する
加算するのは,今回でいえば共有するものが2つあるからって感じ
誤差自体というか傾きは重みを共有している分だけ変化することになる(共有するってことはそういうこと),それぞれで更新されるので
'''
params, grads = params[:], grads[:] # copy list
while True:
find_flg = False
L = len(params) #
for i in range(0, L - 1):
for j in range(i + 1, L):
# 重みを共有する場合
if params[i] is params[j]: # 何番目のレイヤー同士が一緒かをみてる・ここで重みが同じか判定(is 演算子はオブジェクトが同一か判定します) == は値
grads[i] += grads[j] # 勾配の加算
find_flg = True
params.pop(j) # 取り除く(レイヤーの集合から)
grads.pop(j)
# 転置行列として重みを共有する場合(weight tying)
elif params[i].ndim == 2 and params[j].ndim == 2 and \
params[i].T.shape == params[j].shape and np.all(params[i].T == params[j]):
grads[i] += grads[j].T
find_flg = True
params.pop(j)
grads.pop(j)
if find_flg: break # popするので,これでよい(各要素の最初の部分だけみることになるけど)
if find_flg: break
if not find_flg: break # 共通部分がない場合
return params, grads
ここでポイントになるのはまずpythonのimutableとmutableの話
pythonは,配列をそのまま=でつなぐと
a = [1, 2, 3, 4]
b = a
a[0] = 2
# bも変わる
となるのは有名?な話,ここではその性質を利用
その性質を利用することで重みを共有できるのか!
それがこの部分
class SimpleCBOW():
'''
シンプルなCBOWのクラス作成
関数としてmatmulを使うことにする
'''
def __init__(self, vocab_size, hidden_size): # ここでの注意点は隠れ層は入力層より小さくしないとだめ
V, H = vocab_size, hidden_size
# 重みの初期化
# 後々単語の分散表現として使う
W_in = 0.01 * np.random.randn(V, H).astype('f')
W_out = 0.01 * np.random.randn(H, V).astype('f') # 今回は出力はone-hotで出てくるから入力と出力は同じ数!
# レイヤー作成
self.in_layer0 = MatMul(W_in) # contextsは2つしかないので,入力の重みは2つ準備
self.in_layer1 = MatMul(W_in)
self.out_layer = MatMul(W_out)
W_inをあえて同じところに代入することで,同じ重みを共有できる
次に疑問になるのが更新方法
共有しているということは,どうやって重みを更新するんだろうかという話に...
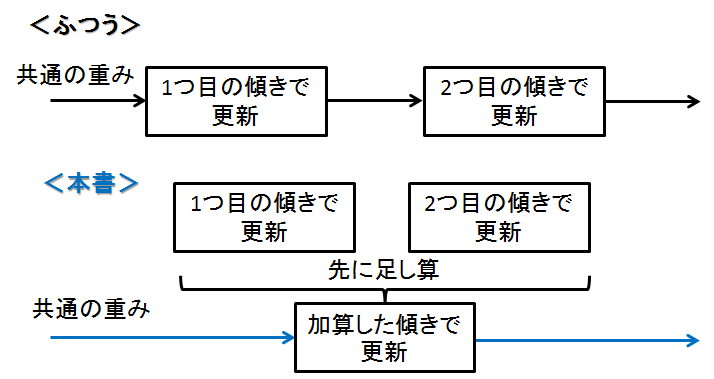
答えは,計算した傾きを加算し,まとめて更新する!!
共有しているので,それぞれの傾き使い重みを更新しそう(下記イメージ),
それは本書でも述べられているようにAdam等がうまく動かなくなるのを避けるため!
しかも,同じ重みを使っているので一個更新すれば,もう片方も勝手に更新されるという...
何て良くできているんだ!!!
これがポインターの概念ですかね
あと,optimizerのAdamの部分
ここで
# たぶんだけど,イタレーション回数が増えるにつれて,更新量が小さくなるようにしているはず(下の方のmainで確認済み)
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
ってしてて
なんでαを固定にしていないのだろうかってなった(確か論文は固定してた気がする)
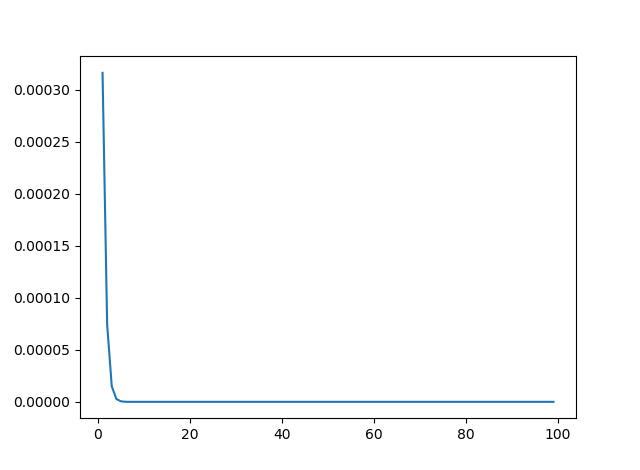
これは,イタレーションの回数が増える毎に,かけるものが小さくなるようにしてる(最初は学習率大きく,徐々に小さくの考え方)
僕のgithubの3rdの中のNN_ch3を実行してすれば,イタレーション回数が大きくなるごとに小さくなる様子が分かる
それが下記グラフ
疑問点
-
Adam等を追加で調べたのでその際の参考を載せておく
https://qiita.com/tokkuman/items/1944c00415d129ca0ee9 -
尤度の話
後少し気になったのが最後の方に出てくる尤度
この尤度での話を調べていたら,ピンポイントの話が載っていたのでこれを参考に!
NNにlog使うのって,最尤推定から来てるのか!,てっきり逆伝播から来てるのかと
- 最後の方ででていた確率の独立について
今回最後の部分で(Skip-gramモデルを紹介しているところ)が少し気になった
本書では,条件付き確率を仮定しているというところ
これは,$\omega_t$が観測されたときに,$\omega_{t-1}$を予測する結果に,$\omega_{t+1}$を予測した結果は関係ないってこと
言い換えれば,$\omega_t$が観測されたときに,$\omega_{t-1}$になったからといって,$\omega_{t+1}$になりやすいわけではないってこと
Chapter4(word2vecの拡張)
概要
前章のword2vecをどうやって高速に行うかの話
- Embedding layerの導入
- Negative samplingの導入
この2つがポイント
個人的にはどうやって計算回数を減らすかが分かればこの章の難易度はそこまで高くないはず
- one-hot vectorだから1以外のところの計算しなくていいよね
- 多値じゃ厳しい...から二値でよいよね
という考えから来ている
プログラム
プログラムでつっかかったところは,p139の加算のところ
class Embedding:
'''
入力層のMatmulの代替え
'''
def __init__(self, W):
self.params = [W] # このくくる理由は前述したとおり
self.grads = [np.zeros_like(W)]
self.idx = None
def forward(self, idx):
W, = self.params
self.idx = idx # どれを取り出すのか保存しておく
out = W[idx] # 取り出しただけ
return out
def backward(self, dout):
dw, = self.grads # 取り出し
dw[...] = 0.0 # そのまま値をリセット
# print('dw = {0}'.format(dw)) 0になります
for i, word_id in enumerate(self.idx): # idを取り出す
dw[word_id] += dout[i]
# 加算なのはrepeatノードとして考えてもそうですが,Matmulの一部の動作を取り出しているので,足し算しないと話がおかしくなります
# matmulを実際に同じ要素を含む形で書いてみると加算理由がわかるかと思います
# ちなみにこれNoneなのはこれ以上逆伝播する必要がないからです
return None
となるのはMatmulで考えるとわかる
結局Matmulだと,同じ要素のところに値が入ることになるから
実際に手で書いて確認してみるといいかも
後はこれといってつまったところはないけど
negativesamplingとるところは少し気になったのでプログラムを見てみると
class UnigramSampler:
'''
negative sampleをとるクラス
'''
def __init__(self, corpus, power, sample_size):# corpusはコーパス,powerは0.75(全然出てこないやつの確率を多少上げる),samplesizeはいくつnegativesampleとるか
self.sample_size = sample_size
self.vocab_size = None
self.word_p = None
counts = collections.Counter() # やる意味わからんけど辞書作成
for word_id in corpus:
counts[word_id] += 1 # 出現回数記録
vocab_size = len(counts) # 語彙数
self.vocab_size = vocab_size
self.word_p = np.zeros(vocab_size) # 出現確率
for i in range(vocab_size):
self.word_p[i] = counts[i]
self.word_p = np.power(self.word_p, power) # 0.75乗する
self.word_p /= np.sum(self.word_p) # 確率分布
def get_negative_sample(self, target): # targetで正解データをもらえる
batch_size = target.shape[0] # しつこいけど行がバッチ数に対応している!
negative_sample = np.zeros((batch_size, self.sample_size), dtype=np.int32) # 型はint型でオッケー
for i in range(batch_size): # バッチサイズ分だけターゲットがあるので
p = self.word_p.copy()
target_idx = target[i] # ターゲットがどのidなのかを取得
p[target_idx] = 0 # そこの取得確率を0にする
p /= p.sum() # sum,もう一回和をとって割り算
negative_sample[i, :] = np.random.choice(self.vocab_size, size=self.sample_size, replace=False, p=p) # 確率分布に従って選ぶ(語彙数
return negative_sample # idが変える # バッチサイズ×sample_sizeになる
こんな感じになっている
ポイントは,ターゲットは選ばないように,そこの確率分布は0にしているところ
後は丁寧に和を取り直してるところかと
後は全体的に重みを共有しているってところを忘れないようにすることか
出力層と入力層それぞれで重みは共有されているのは,
各レイヤーのプログラムの宣言部(4th/NN_ch4.py)
以下のプログラムではW_inのところの話
class CBOW:
'''
ネットワークの作成
'''
def __init__(self, vocab_size, hidden_size, window_size, corpus):
V, H = vocab_size, hidden_size
# 重みの初期化
W_in = 0.01 * np.random.randn(V, H).astype('f') # 正規分布
W_out = 0.01 * np.random.randn(V, H).astype('f')
# レイヤ作成
self.in_layers = []
for i in range(2 * window_size): # コンテキストの数に応じて(windowsizeが1なら両サイドあることになるので2倍)
layer = Embedding(W_in) # 同じ重みを参照する
self.in_layers.append(layer)
self.ns_loss = NegativeSamplingLoss(W_out, corpus, power=0.75, sample_size=5)
layers = self.in_layers + [self.ns_loss] # これで要素が足し算される
# 各レイヤーの重みをまとめておく
self.params, self.grads = [], []
for layer in layers:
self.params += layer.params
self.grads += layer.grads
W_outのところは(4th/layers_ch4.py)
class NegativeSamplingLoss():
'''
Negative sampling 付きの最終レイヤーを作成
'''
def __init__(self, W, corpus, power=0.75, sample_size=5):
self.sample_size = sample_size # 何個negativesamplingを行うのか
self.sampler = UnigramSampler(corpus, power, sample_size) # ネガティブサンプリング器作成
self.loss_layers = [SigmoidWithLoss() for _ in range(sample_size + 1)] # 省略できるんだ..iとか知らなかった,レイヤー作成
self.embed_dot_layers = [EmbeddingDot(W) for _ in range(sample_size + 1)] # レイヤー作成 +1してるのは正解の分,重み共有される
self.params, self.grads = [], [] # ここはいつも通りに収納するためのリスト
for layer in self.embed_dot_layers:
self.params += layer.params
self.grads += layer.grads
で分かる
つまり,W_inとW_outはそれぞれたくさんあるように見えても,それぞれは一緒だということ
(W_inとW_outはもちろん違いますが)
で,ポイントは
Matmulの計算をどう近似するか
Softmaxの計算をどう近似するか
ってこと
Embeddingを実装しているけどやっていること自体は動作処理を軽くするためのものであることが分かればよいと思う
疑問点
改良点が中心だったので,理論的には特になし!
改良点
pickleを使おうってなってますが
なんとなく,pandas使ってます,こんな感じ
それに応じてp165のevaluateのプログラムもいじってます
# 単語の分散を見てみる
word_vecs = model.word_vecs
# wordvec用
word_vecs_pandas = pd.DataFrame(word_vecs)
# word_to_id 用
word_to_id_pandas = pd.io.json.json_normalize(word_to_id)
# id_to_word 用
id_to_word_pandas = pd.io.json.json_normalize(id_to_word)
name_list = ('word_vecs', 'word_to_id', 'id_to_word')
for i, item in enumerate(word_vecs_pandas, word_to_id_pandas, id_to_word_pandas):
item.to_csv(name_list[i] +'_data.csv')
最後に
前半終了!
次からいよいよ本題のRNNへ行きます