こんにちわ。Electric Blue Industries Ltd.という、ITで美を追求するファンキーでマニアックなIT企業のマッツと申します。TensorFlow.jsでDeepLearningのチュートリアル「Making Predictions from 2D Data」の詳細解説の前半です。
これはTensorFlow.JSの公式サイトにある「TensorFlow.js — Making Predictions from 2D Data」をコードの中に記載したコメントで詳細に解説したものです。解説の利便性によりコードの部分の位置関係は変更してありますが、内容に変化はありません。実際に動作するデモはこちらで見られます。
1. コード
1.1. html
ライブラリを読み込んでDeep LearningのためのJavaScriptを実行するHTMLです。
展開してコードを見る
<html>
<head>
<meta charset="utf-8">
<meta http-equiv="X-UA-Compatible" content="IE=edge">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<title>TensorFlow.js Tutorial - Making Predictions from 2D Data</title>
<!-- Import TensorFlow.js (TensorFlow.jsライブラリ本体を読み込みます) -->
<script type="text/javascript" src="https://cdn.jsdelivr.net/npm/@tensorflow/tfjs@1.0.0/dist/tf.js"></script>
<!-- Import tfjs-vis (TensorFlow.js向けの可視化ライブラリを読み込みます) -->
<script type="text/javascript" src="https://cdn.jsdelivr.net/npm/@tensorflow/tfjs-vis@1.0.2/dist/tfjs-vis.umd.min.js"></script>
<!-- Import the main script file (下記に解説するJavaScriptを読み込みます)-->
<script type="text/javascript" src="script.js"></script>
</head>
<body>
</body>
</html>
1.2. JavaScript
上記のHTMLにインクルードされてDeep Learning処理を行うJavaScriptです。
展開してコードを見る
/******************************************************************
TensorFlow.js — Making Predictions from 2D Data
url: https://codelabs.developers.google.com/codelabs/tfjs-training-regression/index.html#0
filename: script.js
copyrighted to: tensorflow.org
composed by: Mats (Electric Blue Industries Ltd.)
description: 車のスペック情報から「燃費」「馬力」のデータを学習し、それらの相関を学習させる
******************************************************************/
async function run() {
//******************************************************************
// 1. getData: 元データをgetDataを使って読み込み対象アイテムのみフィルター(元データプロット用)
//******************************************************************
// 非同期で元データを取得(getDataは下で関数として定義)
// なお、取得するデータは [{0:a, 1:b, 2:c}, {0:d, 1:e, 2:f}]のように、各クルマのスペック情報を持つオブジェクトが要素になった配列データ
const data = await getData();
// 読み込んだ元データであるdataから項目抽出して、座標情報オブジェクトを各要素とする配列として新たに格納
const values = data.map(d => ({
x: d.horsepower,
y: d.mpg,
}));
// TensorFlowJSの可視化ライブラリで元データの位置をプロットする
tfvis.render.scatterplot(
// 表のタイトルの指定
{name: 'Horsepower vs Miles Per Gallon'},
// 上記で生成した座標情報オブジェクトを各要素とする配列を指定
{values},
// 表のx軸y軸のタイトルおよび表の高さを指定
{
xLabel: 'Horsepower',
yLabel: 'Miles Per Gallon',
height: 300
}
);
// 元データを非同期で読み込む関数
async function getData() {
// 非同期でクルマのスペックデータ(内容はオブジェクトを要素に持つ配列のフォーマットをしている)を取得しcarsDaraに格納
const carsDataReq = await fetch('https://storage.googleapis.com/tfjs-tutorials/carsData.json');
// 読み込んだデータをJSON形式として読んで各クルマのスペック(オブジェクト)を要素として持つ配列carsDataとして格納
const carsData = await carsDataReq.json();
// 格納した配列carsDataデータから元データとして用いる2アイテムのみを取得しcleanedとして格納
// map関数は配列の各要素に繰り返し指定された処理を行うので、cleanedはmpgとhorsepowerの情報のみを含むオブジェクトを要素とする配列
// なお、mpgとhorsepowerのどちらかでも空文字の場合はデータから削除しておくfilterをかける
const cleaned = carsData.map(car => ({
mpg: car.Miles_per_Gallon,
horsepower: car.Horsepower,
}))
.filter(car => (car.mpg != null && car.horsepower != null));
return cleaned;
}
//******************************************************************
// 2. createModel: モデルの枠組みの作成
//******************************************************************
// モデルを作成(createModelは下で関数として定義)
const model = createModel();
// 上記で作成したモデルの要約情報(Layer Name, Output Shape, # Of Params, Trainable)表示
tfvis.show.modelSummary({name: 'Model Summary'}, model);
// モデル作成の関数定義
function createModel() {
// シーケンシャルモデル(線形回帰モデル)の枠組みの作成
// これはモデルが全体として線形回帰モデルになるという意味でなく、各ニューロンの入出力の関係が y=Σ(wx)+b と書ける線形回帰モデルであるということ
const model = tf.sequential();
// 入力層を追加
model.add(tf.layers.dense({
// 入力は 1x1 のテンソル(=スカラー)
inputShape: [1],
// ユニット(別名:ノード)は1個だけ
units: 1,
// y=Σ(wx)+b となる定数項bであるバイアスを使用する
useBias: true
}));
// ここに中間層を追加した場合にはどうなるのかは別途に言及する
// 出力層を追加
model.add(tf.layers.dense({
// ユニット(別名:ノード)は1個だけ
units: 1,
// y=Σ(wx)+b となる定数項bであるバイアスを使用する
useBias: true
}));
return model;
}
//******************************************************************
// 3. convertToTensor: 学習データを上記モデルに流し込めるようテンソルに変換する
//******************************************************************
// getDataで取得したclean済み配列データを下記で定義したconvertToTensor関数でテンソルに変換(不要なアイテムは同時にフィルター)
const tensorData = convertToTensor(data);
const {inputs, labels} = tensorData;
// 学習データをテンソルに変換する
function convertToTensor(data) {
// tidyを使って計算することで、計算経過で生成される変数をメモリから削除してメモリにゴミを残さない
return tf.tidy(() => {
// (ステップ1) データをシャッフルする
tf.util.shuffle(data);
// (ステップ2) データを配列に格納してから展開してテンソルに変換
// 変数inputに馬力に関するデータ(実際は配列)を格納
const inputs = data.map(d => d.horsepower)
// 変数labelsに燃費に関するデータ(実際は配列)を格納
const labels = data.map(d => d.mpg);
// 上記で作成したインプット値(馬力)の配列を使って Nx1 の行列を生成
const inputTensor = tf.tensor2d(inputs, [inputs.length, 1]);
// 上記で作成される2次元テンソルは下記のような縦長の形
// [[馬力の値1],
// [馬力の値2],
// :
// [馬力の値N]]
// 上記で作成したラベル値(燃費)配列を使って Nx1 の行列を生成
const labelTensor = tf.tensor2d(labels, [labels.length, 1]);
// 上記で作成される2次元テンソルは下記のような縦長の形
// [[燃費の値1],
// [燃費の値2],
// :
// [燃費の値N]]
// (ステップ3) 入力データの値を0から1の間に正規化
// 入力とラベルを最大値と最小値を調べて取得
// 入力である馬力の最大値を取得
const inputMax = inputTensor.max();
// 入力である馬力の最小値を取得
const inputMin = inputTensor.min();
// 出力である燃費の最大値を取得
const labelMax = labelTensor.max();
// 出力である燃費の最小値を取得
const labelMin = labelTensor.min();
// 入力とラベルを正規化
// inputTensor.sub(inputMin)で各入値から最小入力値をひく(=最小値をゼロに落とす) >> (これをAとする)
// inputMax.sub(inputMin)で最大入力値から最小入力値をひく >> (これをBとする)
// 上記の各(A)の値を(B)で割ることで、最大値が1で最小値が0になるよう正規化する
const normalizedInputs = inputTensor.sub(inputMin).div(inputMax.sub(inputMin));
// labelTensor.sub(labelMin)で各入値から最小入力値をひく(=最小値をゼロに落とす) >> (これをA'とする)
// labelMax.sub(labelMin)で最大入力値から最小入力値をひく >> (これをB'とする)
// 上記の各(A')の値を(B')で割ることで、最大値が1で最小値が0になるよう正規化する
const normalizedLabels = labelTensor.sub(labelMin).div(labelMax.sub(labelMin));
return {
// 正規化された値を要素に持つ入力テンソルと出力(ラベル)テンソルを返す
inputs: normalizedInputs,
labels: normalizedLabels,
// 入力と出力(ラベル)の最大値最小値もあとで逆正規化できるよう返す
inputMax,
inputMin,
labelMax,
labelMin,
}
});
}
//******************************************************************
// trainModel: モデルの学習
//******************************************************************
// モデルの学習(trainModelは下で関数として定義)
// awaitとすることでtrainModel関数からreturnがあるまで待機する
await trainModel(model, inputs, labels);
// モデル・入力(インプット)テンソル・出力(ラベル)テンソルを指定してモデルの学習を行う関数
async function trainModel(model, inputs, labels) {
// 学習実行のため、学習方法を指定してモデルをコンパイル
model.compile({
// 最適化法をアダム(=適応モーメント推定法)に指定
optimizer: tf.train.adam(),
// 損失関数をMSE(=平均二乗誤差)に指定
loss: tf.losses.meanSquaredError,
// 学習とテストに用いる指標(この場合は平均二乗誤差)を表す表現を決める
metrics: ['mse'],
});
// バッチサイズ(小分けにグループ分けした学習データに含まれるデータの個数)を28個とする
const batchSize = 28;
// 学習の1手順の回数を50回とする
const epochs = 50;
// epochsで指定した回数の学習手順回数(エポック)になるまで学習を実行する
return await model.fit(inputs, labels, {
batchSize,
epochs,
shuffle: true,
// 学習結果の随時の描画用にTFVISに、コンパイル時に指定した指標の値をコールバックする指定
callbacks: tfvis.show.fitCallbacks(
// 描画する表のタイトル
{ name: 'Training Performance' },
// 描画する指標(ここではlossとmseを改めて指定)
['loss', 'mse'],
{
// 表の高さ
height: 200,
// コールバックのタイミング
callbacks: ['onEpochEnd']
}
)
});
}
// trainModel関数に返り値があった時点で規定したエポックが終了したことになるので「学習が終わった」とコンソールに出力
console.log('Done Training');
//******************************************************************
// testModel: 学習ずみモデルに入力を与えて出力を得て、元データのプロットと重ねて違いを視覚的に見せる
//******************************************************************
// モデルのテスト(testModelは下で関数として定義)
testModel(model, data, tensorData);
function testModel(model, inputData, normalizationData) {
const {inputMax, inputMin, labelMin, labelMax} = normalizationData;
// Generate predictions for a uniform range of numbers between 0 and 1;
// We un-normalize the data by doing the inverse of the min-max scaling
// that we did earlier.
const [xs, preds] = tf.tidy(() => {
// tf.linespaceで0から1までの間に等間隔となる100個の値を生成(0, 0.01, 0.02, 0.03,・・, 0.98, 0.99)し格納
// なお、tf.linspace()によって生成されるのは配列ではなく「Array.from()で配列化できるオブジェクト」である
const xs = tf.linspace(0, 1, 100);
// 上記で生成した100個の数値を要素にもつ行列を生成し、学習したモデルに予測値として出力させる
const preds = model.predict(xs.reshape([100, 1]));
// モデルの入出力は共に正規化されているので、これを元に戻す計算を行う
const unNormXs = xs.mul(inputMax.sub(inputMin)).add(inputMin);
const unNormPreds = preds.mul(labelMax.sub(labelMin)).add(labelMin);
// 上記で非正規化されたデータは100行1列の行列になっているので、これらを単なる配列の形にする
return [unNormXs.dataSync(), unNormPreds.dataSync()];
});
// 学習データのポイント(座標)を配列として格納
// mapは配列を受け取って、指定した処理を行う
// ここでは入力値inputDataとして「座標情報を持ったオブジェクト」を要素にもつdataを代入しているので、各要素から馬力と燃費のデータを読んで
// ポイント(座標)をオブジェクト形式で表す要素を持つ配列の各要素として持たせている
const originalPoints = inputData.map(d => (
{
x: d.horsepower,
y: d.mpg,
}
));
// 学習させたモデルを使って算出した予測値のポイント(座標)をオブジェクト形式で表す要素を持つ配列として格納
const predictedPoints = Array.from(xs).map((val, i) => {
return {
x: val,
y: preds[i]
}
});
// 上記で得た予測値および学習データ値のポイントをTFVISに渡してプロット表示
tfvis.render.scatterplot(
{
// 表のタイトル
name: 'Model Predictions vs Original Data'
},{
// originalPointsとpredictedPointsはポイントの座標をJSONで表現した文字列を要素に持つ配列
values: [originalPoints, predictedPoints],
series: ['original', 'predicted']
},{
// 縦軸と横軸の名称、表の高さ
xLabel: 'Horsepower',
yLabel: 'Miles Per Gallon',
height: 300
}
);
}
}
document.addEventListener('DOMContentLoaded', run);
2. 実行結果
TensorFlow.jsの処々の情報は可視化ライブラリであるTF-VISを使って表やグラフで可視化することができます。下記は上記のコードを実行した際に表示された情報です。
2.1. 学習データのプロット
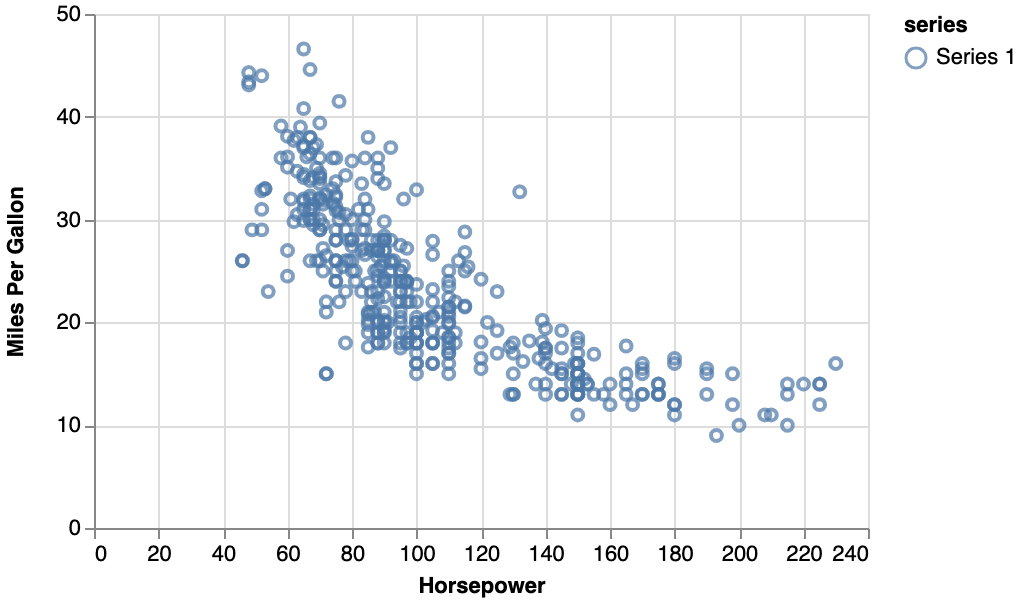
学習データの「馬力(横軸:Horsepower)」と「燃費(縦軸:Miles Per Gallon)」の関係をプロットしたプロットチャートです。これを見ると、学習すべき馬力と燃費の関係は互いに反比例する関係にあることが伺えますが、直線的なの反比例関係ではなく、穏やかなカーブを描くような反比例であることが伺えます。
2.2. 学習の進行状況
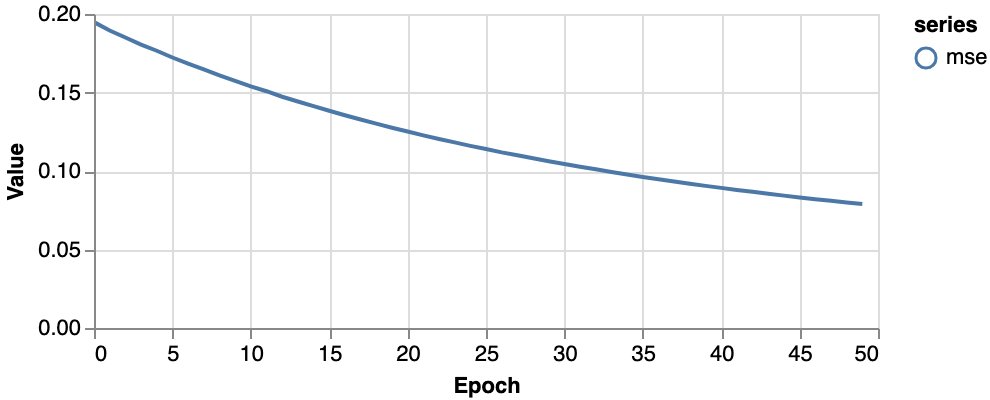
下記は損失関数の値です。損失関数をmse(= Mean Squared Error = 平均二乗誤差)に指定し、学習のエポックごとにその値が降下していっていることがわかります。このコードでは学習を50エポックまでと指定したので横軸は50までとなっています。損失関数の値がこれで十分なのかどうかと言う話は別途に言及します。
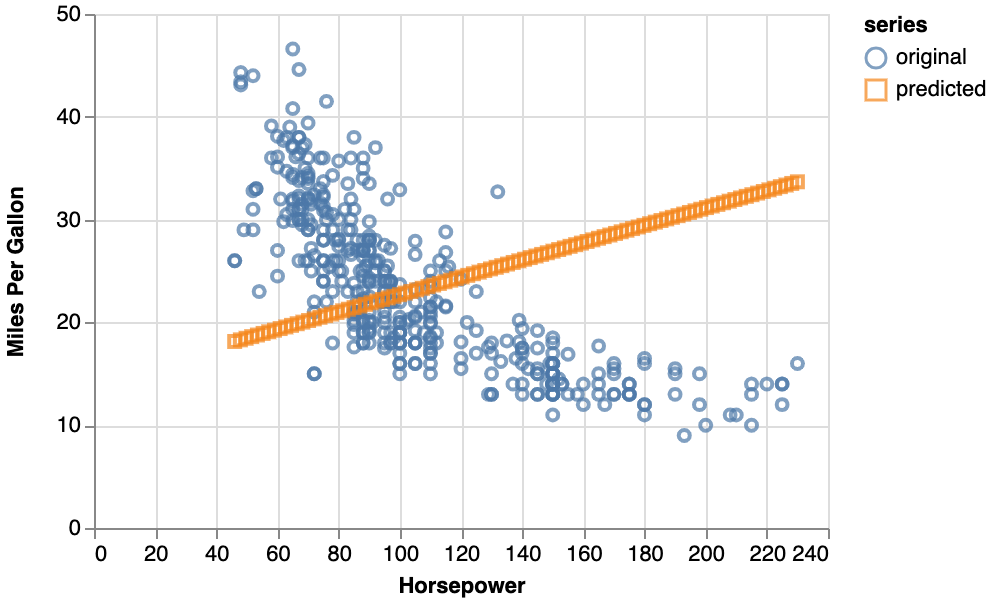
2.3. 学習したモデルによる出力予測
学習させたモデルに入力として「馬力」の値を与え、その出力として「予測(predict)される燃費」を得ました。その関係を先ほどの学習データのプロットチャートに重ねて表示したものがこれです。学習したモデルが出力したオレンジ色の点が直線的に並んでいます。
3. モデルの精度を高める
TensorFlow.orgのチュートリアルは上記で終わりとなっているのですが、上記で記述したコードと作成したモデルについて、「これで良いのでしたっけ?」と言う視点で考察と改造を行います。
と言うのは、学習データの「馬力(横軸:Horsepower)」と「燃費(縦軸:Miles Per Gallon)」の関係は直線的なの反比例関係ではなく、穏やかなカーブを描くような反比例であることが伺えます。しかしながら、学習させたモデルが予測した関係は直線的な正比例の傾向を示しています。この相違によってモデルの予測精度が十分ではなくなっていると推測できます。もっと、正確に入力と出力の関係を学習させるにはどうすればイイのか?
なお、上記で作成したモデルによる予測の損失関数の値(MSE: 平均二乗誤差)は0.7から0.8でした。
3.1. 出力層に非線形活性化関数を適用する
// 出力層を追加
model.add(tf.layers.dense({
// ユニット(別名:ノード)は1個だけ
units: 1,
// y=Σ(wx)+b となる定数項bであるバイアスを使用する
useBias: true,
// 出力を線形にしないために非線形活性化関数を被せる(データに対してsoftplusが最適)
activation: 'softplus'
}));
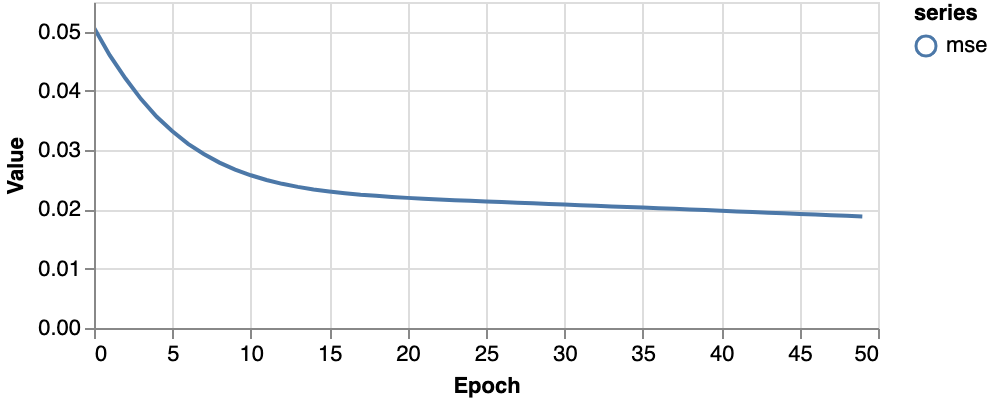
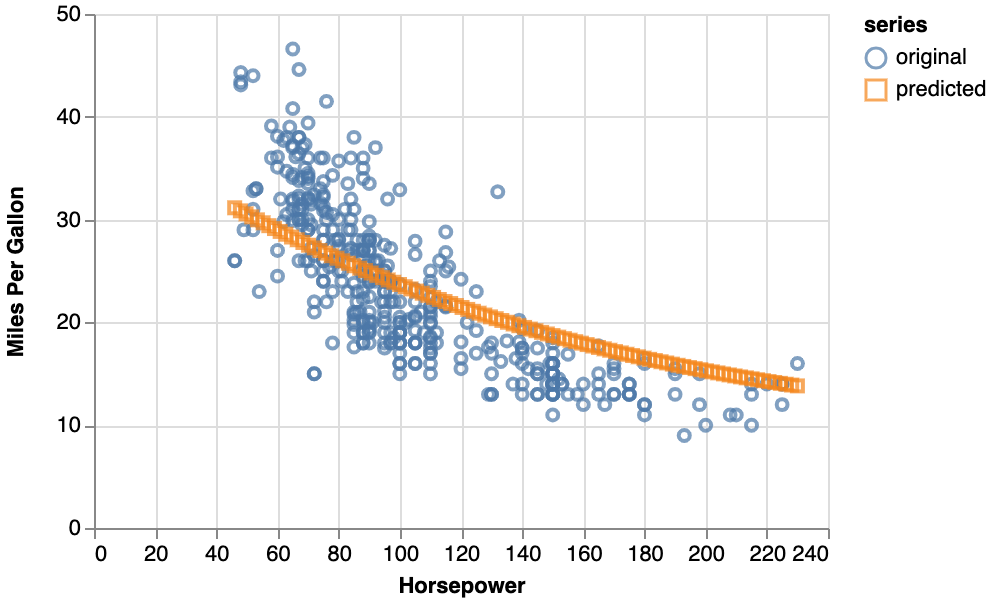
そうすると、MSEの値は0.0189程度まで下がり、回帰の精度が向上しました。
回帰を表す予測値の描くオレンジの線も曲線になり、非線形回帰ができています。
3.2. 中間層を追加する
しかしながら、回帰曲線の曲がり具合が「硬い」ように見受けられ、この曲線をもっと柔らかくしたいように思います。そこで、モデルに中間層を加えます。中間層を加える行為というのは、イメージで言って「回帰曲線に急激な曲がりを加えられるようにすることを可能にする」行為です。また、ユニット(=ノード)の数は回帰曲線の曲げ具合を制御する「コントロールポイント」の数のイメージで、コントロールポイントが多いと回帰曲線を細かく曲げられます。ベジェ曲線のコントロールポイントと似ています。
// ここに中間層を追加した場合にはどうなるのかは別途に言及する
model.add(tf.layers.dense({
// ユニット(別名:ノード)は16個
units: 16,
// y=Σ(wx)+b となる定数項bであるバイアスを使用する
useBias: true
}));
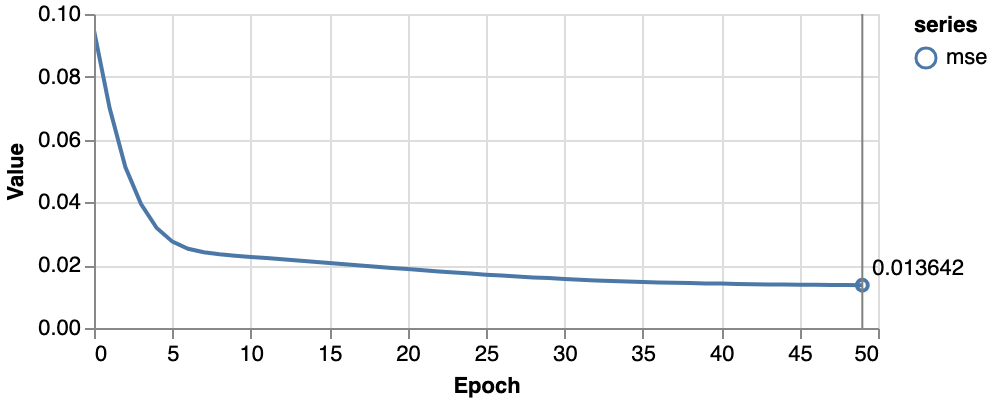
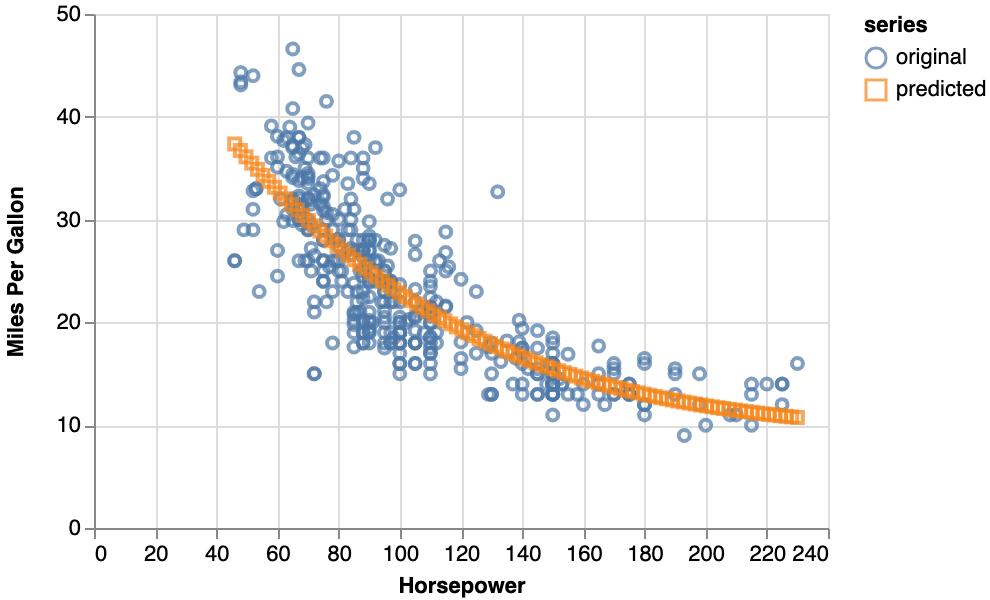
そうすると、MSEの値は0.0136程度まで下がり、回帰の精度が向上しました。
回帰曲線の曲がり具合も強くなりました。
3.3. 中間層のノード数を増やす
回帰曲線の曲がり具合が柔軟になったので、更にユニットを増やして32個にします。
// ここに中間層を追加した場合にはどうなるのかは別途に言及する
model.add(tf.layers.dense({
// ユニット(別名:ノード)は32個
units: 32,
// y=Σ(wx)+b となる定数項bであるバイアスを使用する
useBias: true
}));
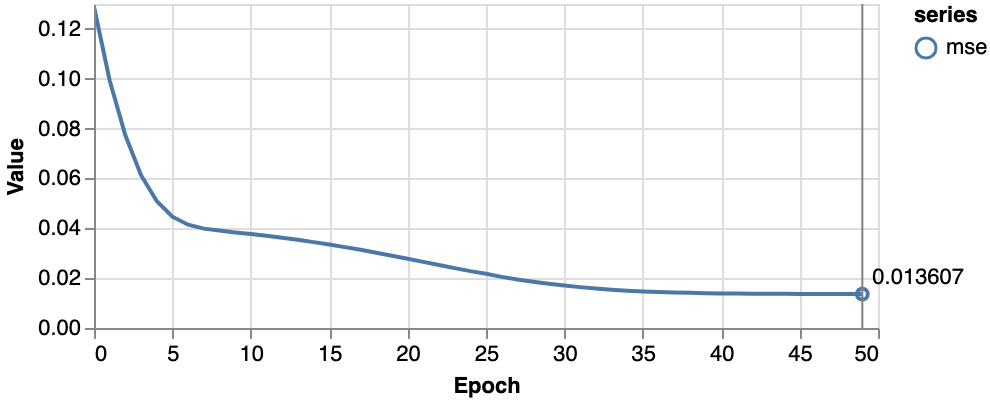
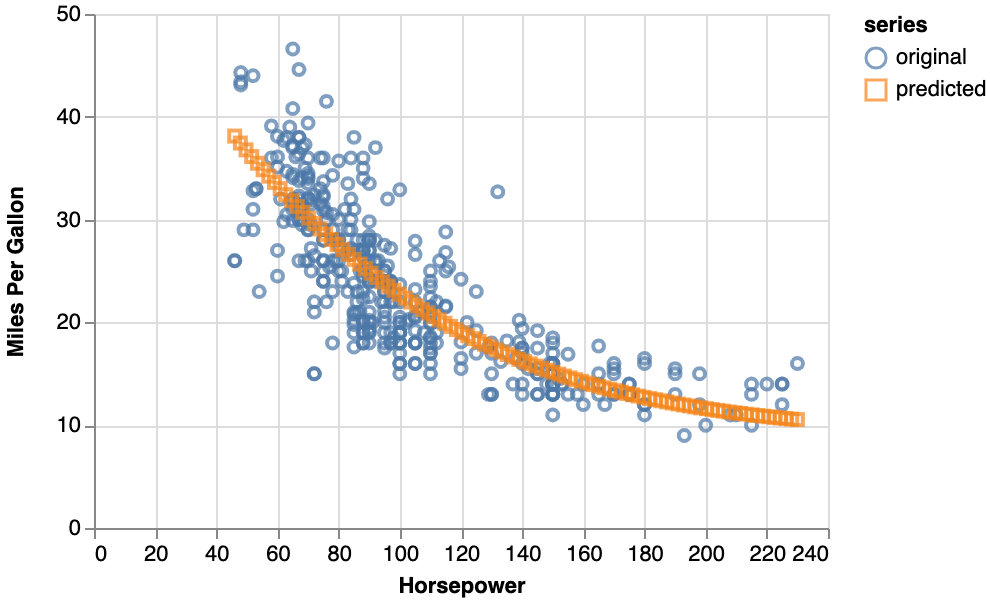
そうすると、MSEの値は0.0136程度でユニット数16の時とほぼ変わらず、回帰の精度は向上しません。
描かれる回帰曲線もほぼ変わっていません。
これは、「ユニットを増やすことで回帰曲線を細かく曲げられるようになったが、実際に細かく曲げても『右に曲げれば左から遠くなり、左に曲げれば右から遠くなり』という収束点に既に到達したから」と考えられます。このように、ユニット数を増やすのは予測精度を高めるには有効ですが、無駄に増やすと計算処理量ばかりが増えて精度は向上しないので、学習させるデータの特性を理解しながら学習させることが肝要です。
追伸: Machine Learning Tokyoと言うMachine Learningの日本最大のグループに参加しています。作業系の少人数会合を中心に顔を出しています。基本的に英語でのコミュニケーションとなっていますが、能力的にも人間的にもトップレベルの素晴らしい方々が参加されておられるので、機会がありましたら参加されることをオススメします。