はじめに
競プロしてたらLCA求めたくなって、それにダブリングが必要だったので理解したので記事にしました
ダブリングとは
用途
ダブリングというのは、「連続した状況がある時、ある時点$i$においてその$K$回先の状況を求めるのには$O(K)$の時間がかかる場合に有効な手段です
この記事では、下のようなグラフの、「要素$i$から$K$回進んだ場所」を求めることを目的にしようと思います。(剰余とか使えば$O(1)$で解けちゃいそうですが今回はダブリングを使って解きます)
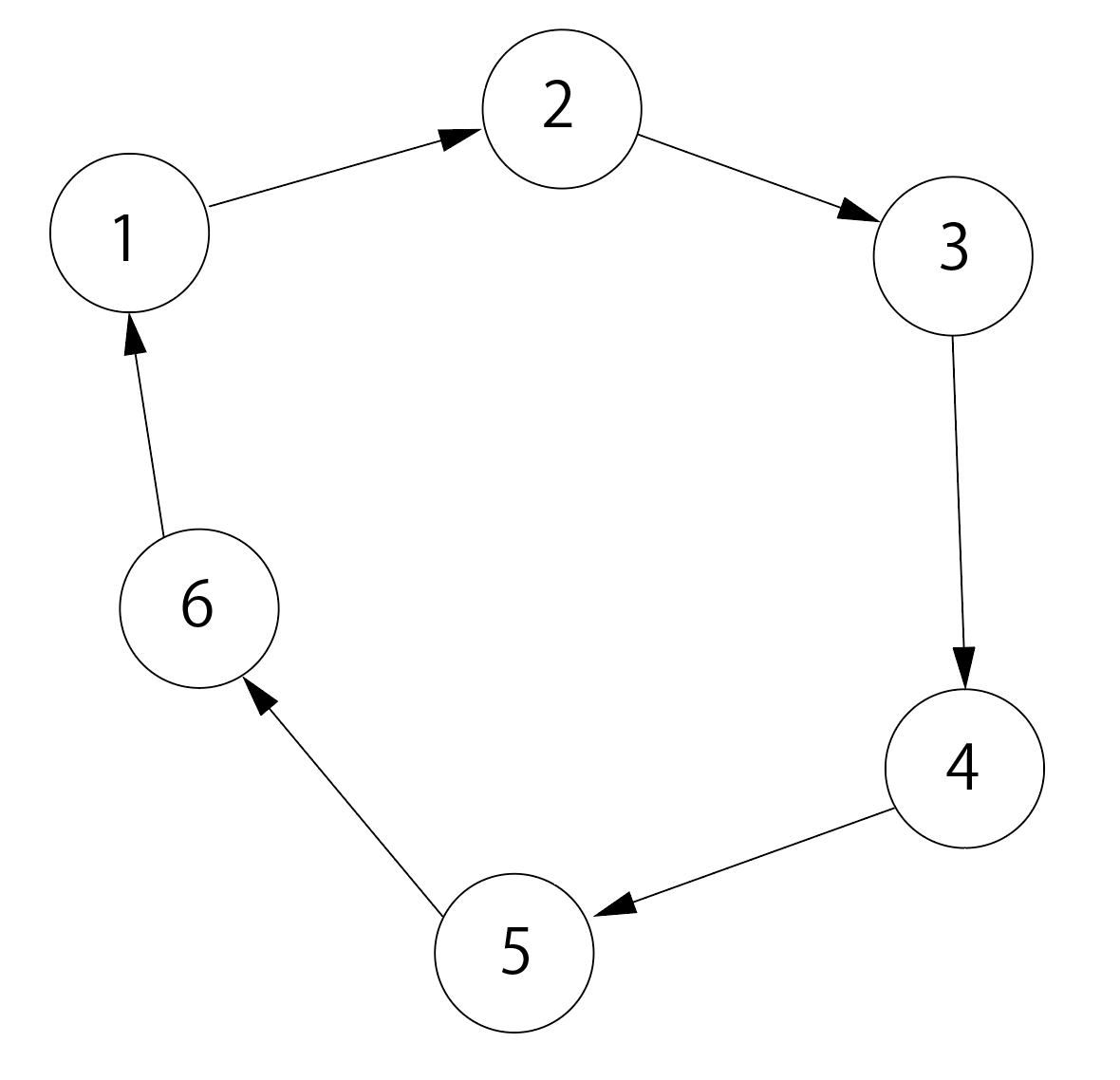
計算量
- 前処理:$O(N logN)$
- クエリ(ある時間の$K$回先の状況を求める):$O(logK)$
ダブリングの考え方
前提
ダブリングは、前処理で次のようなテーブルを作成し、クエリではそのテーブルを利用して求める値を出します
doubling[k][i] := 状態$i$の、$2^k$回先の状態
前処理
さて、前処理ではテーブルの構築をするので、どうにかして漸化式を立てられれば良さそうです。
ここで、「$i$回目の状態の、$2^{k+1}$回先の状態」というのは、言い換えれば
「$i$回目の状態の$2^k$回先の状態」の$2^k$回先の状態
と言い換えられます。このことから、漸化式は次のようになります
$$
doubling_{k+1, i} := doubling_{k, doubling_{k,i}}
$$
ソースコードだとこんな感じ
dp[k+1][i] = dp[k][dp[k][i]];
これがものすごく重要
(ここで、状態を表すdoubling[k][i]が添字に使われていますが、これも結局のところ配列の添字にすぎない(0≤doubling[k][i]<N)ので、問題ありません)
あとはk=0の時の初期値がわかれば完成です
これは、グラフを深さ優先探索をする時に一緒にできそうですね
これらのことを踏まえると、前処理は以下のような実装になります(C++)
using Graph = vector<int>; // 今回、辺は要素一つにつき一つしかないので1次元配列で十分
void dfs(Graph &G, vector<int> &dist, vector<vector<int>> &doubling, int now){
// 今回、辺は要素一つにつき一つしかないのでループはしない
if (dist[G[now]] != -1) return; //訪問済み
doubling[0][now] = G[now];
dfs(G, dist, doubling, G[now]); // 再起的に探索
}
int main(void){
int n; // 要素数
cin >> n;
Graph G(n); // グラフ
/*
グラフの入力処理
*/
int K = 1; // 2^K >= nとなる最小のK(=log(n)を求めたい)
while((1 << K) < n) ++K;
vector<vector<int>> doubling(K, vector<int>(n, -1)); // ダブリングのテーブル。-1で初期化
vector<int> dist(n, -1); // 要素0からの距離。今回はDFSのマーカーとして使う
dist[0] = 0;
dfs(G, dist, doubling, 0); // dfsをしながら doubling[0] の部分を初期化
// 漸化式をもとにテーブルを構築
for(int k = 0; k + 1 < K; ++k){
for(int i = 0; i < n; ++i){
if (doubling[k][i] == -1) doubling[k+1][i] = -1; // 今回はここに入ることはないけれど、入る場合もある
else doubling[k+1][i] = doubling[k][doubling[k][i]]; // 漸化式をそのまま
}
}
}
クエリ処理
さて、ではクエリ処理をしていきましょう
クエリで行いたいのは、「$i$番目の状態から$K$回進んだ時の状態」を求めることです。これを達成することを考えます。
まず、Kを2進数にした時の、右からi番目のビットを$B_i$、ビット数を$A$とすると、
K = B_0 2^0 + B_1 2^1 + B_2 2^2 + ...
と表せます
10を例に図で表すとこんな感じ
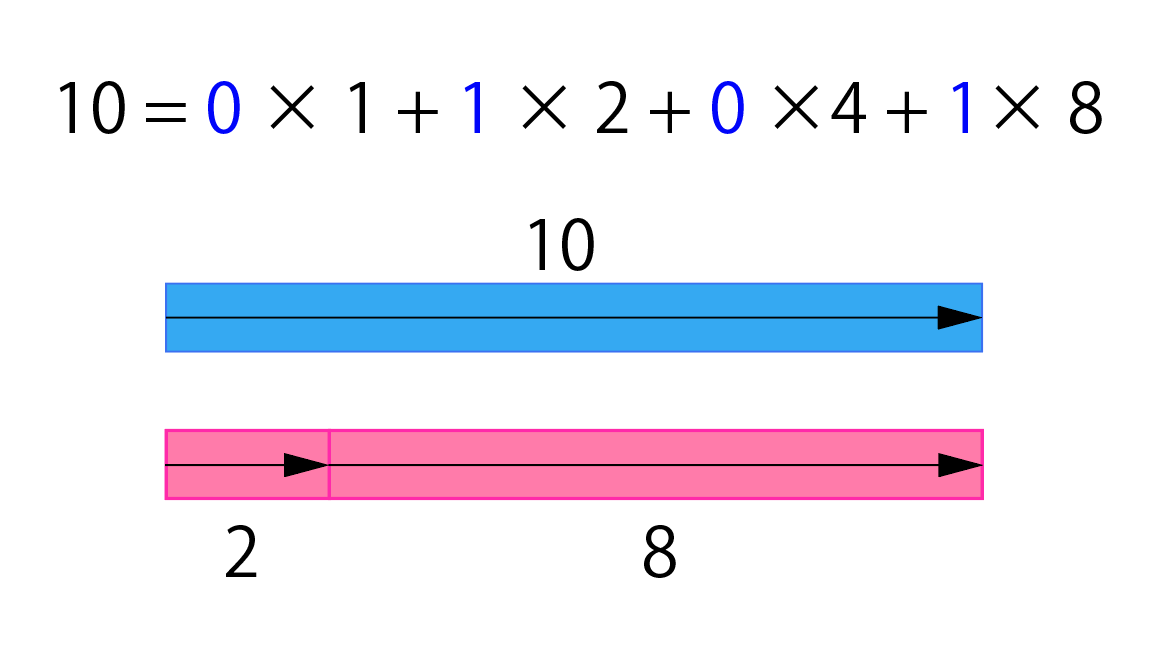
つまり、$K$回進むというのは、
$B_0 2^0$回進んで、$B_1 2^1$回進んで、$B_2 2^2$回進んで...
の繰り返しです。
そして、(ある時点$i$から)$2^k$回進んだ時の状況は、 doubling[k][i] ですから、これを使えば、$K$回進むという動作を$O(logK)$で達成できます
では、ここまでを踏まえて、クエリ処理のソースコードを書いてみましょう
int s; // スタート地点
int t; // 進む回数
cin >> s >> t;
for(int k = 0; k < K; ++k){ // ビット全探索チックに探索
if ((1 << k) & t){
s = doubling[k][s];
}
}
前処理よりも圧倒的に簡単(なソースコード)ですね
ダブリングの使用例
ダブリングは、LCAを求める時によく使われます。
LCAというのは、木において、二つの要素の共通の親のうち根から最も遠いもののことです。
ここでは詳しい解説は割愛します。(このサイトがよく分かり易いです)
簡単に何をやっているのかを説明すると、
今までは「地点$i$から$K$回進めた状態を求める」ことをしていたのに対して、この問題では「地点$i$からある条件を満たす状態$T$にするための回数の最小値$K$」を求めています。
そして、この最小値$K$は、二進数にした時の最上位ビット(最も左側のビット)から求めていくことで、二分探索法のように求めることができます。
まとめ
いかがでしたでしょうか
まとめると、ダブリングは
- 前処理の段階で$O(NlogN)$で
doubling[k+1][i] := doubling[k][doubling[k][i]]を満たすテーブルを作成 - クエリでは$O(logK)$で「ある状態から$K$回進んだ状態」を求める
アルゴリズムでした。
この記事を通じてダブリングの理解が深まってくれたら嬉しいです。
おまけ(ソースコードまとめ)
using Graph = vector<int>; // 今回、辺は要素一つにつき一つしかないので1次元配列で十分
void dfs(Graph &G, vector<int> &dist, vector<vector<int>> &doubling, int now){
// 今回、辺は要素一つにつき一つしかないのでループはしない
if (dist[G[now]] != -1) return; //訪問済み
doubling[0][now] = G[now];
dfs(G, dist, doubling, G[now]); // 再起的に探索
}
int main(void){
int n; // 要素数
cin >> n;
Graph G(n); // グラフ
/*
グラフの入力処理
*/
int K = 1; // 2^K >= nとなる最小のK(=log(n)を求めたい)
while((1 << K) < n) ++K;
vector<vector<int>> doubling(K, vector<int>(n, -1)); // ダブリングのテーブル。-1で初期化
vector<int> dist(n, -1); // 要素0からの距離。今回はDFSのマーカーとして使う
dist[0] = 0;
dfs(G, dist, doubling, 0); // dfsをしながら doubling[0] の部分を初期化
// 漸化式をもとにテーブルを構築
for(int k = 0; k + 1 < K; ++k){
for(int i = 0; i < n; ++i){
if (doubling[k][i] == -1) doubling[k+1][i] = -1; // 今回はここに入ることはないけれど、入る場合もある
else doubling[k+1][i] = doubling[k][doubling[k][i]]; // 漸化式をそのまま
}
}
int s; // スタート地点
int t; // 進む回数
cin >> s >> t;
for(int k = 0; k < K; ++k){ // ビット全探索チックに探索
if ((1 << k) & t){
s = doubling[k][s];
}
}
}