経緯
これまで Python で小規模な数値計算をやってきたが、
- 高速らしい
- 可視化も良さそう
なので Julia を試してみる
インストール
JuliaPro (ディストリビューション)
https://juliacomputing.com/products/juliapro.html
Personal は無料、要ユーザー登録
インストール後、 anaconda の Jupyter notebook を起動すると Julia のカーネルが利用できるようになっている
REPL
Pkg.update() # けっこうかかる
Pkg.add("Plots") # 可視化、フロントエンド
Pkg.add("GR") # 可視化、バックエンド
基本的なこと
- (コンマかセミコロンで区切った)一次元配列は縦ベクトル
- 1-origin
- 配列入力に対してはドット(自動的にブロードキャストされる)
sin.( [1, 3, 7] )
Julia言語で計算が遅くなった場合の解決法
http://nbviewer.jupyter.org/gist/genkuroki/1ac59bb3e03eac12945d7040d4f98246
引数渡しの挙動
- 配列はポインタ(参照?)渡し
- 引数が変更される関数には!をつける
実は NumPy でも同じだが、これまで気づいていなかった
# 数字
function f(x) # コピーが渡される
x += 100 # コピーに変更を加える
end
x = 1
f(x)
x # 1 呼び出し元は変更されない
# 配列
function g!(arr) # アドレス(のコピー?)が渡される
arr[:] += 100 # 呼び出し元に変更を加える
end
arr = [1]
g!(arr)
arr # [101] 呼び出し元が変更されている
関数は遅延評価
これも Python と同じ(だが、以下略)
a = 1
return_a() = a # 関数の短い書き方
a = 2
return_a() # 2
様々な実装と処理時間
KdV 方程式 t=1.2 まで計算
Walkley Scheme, Δt = 1e-5
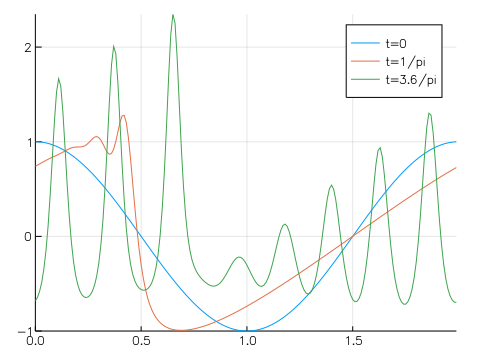
| 言語 | 処理時間 | 倍率 | 詳細 |
|---|---|---|---|
| Python | 19 sec | 1.0x | NumPy convolve1 |
| Julia | 50 sec | 0.4x | デフォルトの conv |
| Julia | 7.0 sec | 2.7x | FastConv2 |
| Julia | 5.6 sec | 3.4x | FastConv + 関数化 |
| Julia | 2.9 sec | 6.6x | FastConv + 関数化 + 型指定 |
| Julia | 3.1 sec | 6.1x | ベクトルの内積 |
| Julia | 230 ms | 82x | for文 |
| Julia | 92 ms | 206x | for文 + SIMD |