はじめに

たまに、「遺伝的アルゴリズムで○○やってみた」という記事をみることがあります。遺伝的アルゴリズムは、コンセプトやロジックがわかりやすく、初心者にもとっつきやすいアルゴリズムだと思っています。ただ、実際の製品や事例で普通のGAが採用されている例は滅多にない気がしており、実数値GAやるならDEのほうが実装も楽だし性能も高いんじゃない？ということで紹介したいと思います。

ただし、私自身進化計算を追っていたのは数年前のため、情報が古い可能性があります・・・。ご了承ください。

差分進化（Differential Evolution, DE）

差分進化（Differential Evolution, DE）は、StornとPriceによって1995年¹²に提案された、単目的最適化アルゴリズムです。基本的には遺伝的アルゴリズムとほぼ同じ、進化計算の枠組みに含まれるアルゴリズムですが、生物の進化や生物の行動に着想を得ていないところが特徴的です。

GAよりすごい最新アルゴリズムだぜ！って感じではなく、これも相当古いのですが、仕組みがシンプルな割りにそこそこ性能が高く、人気なアルゴリズムです。

DEの流れ

DEは、その名の通り「差分」をとって進化していく（探索を進めていく）アルゴリズムです。

詳細なアルゴリズムについては、Qiitaにも既に記事があるため省略します。以下の記事が分かりやすかったです。
差分進化法でハイパーパラメータチューニング

ここでは、数式を使わずにDEの大体のニュアンスを説明したいと思います。ここでは、説明を簡単にするために、交叉率$C=1.0$とします。

1. 初期化

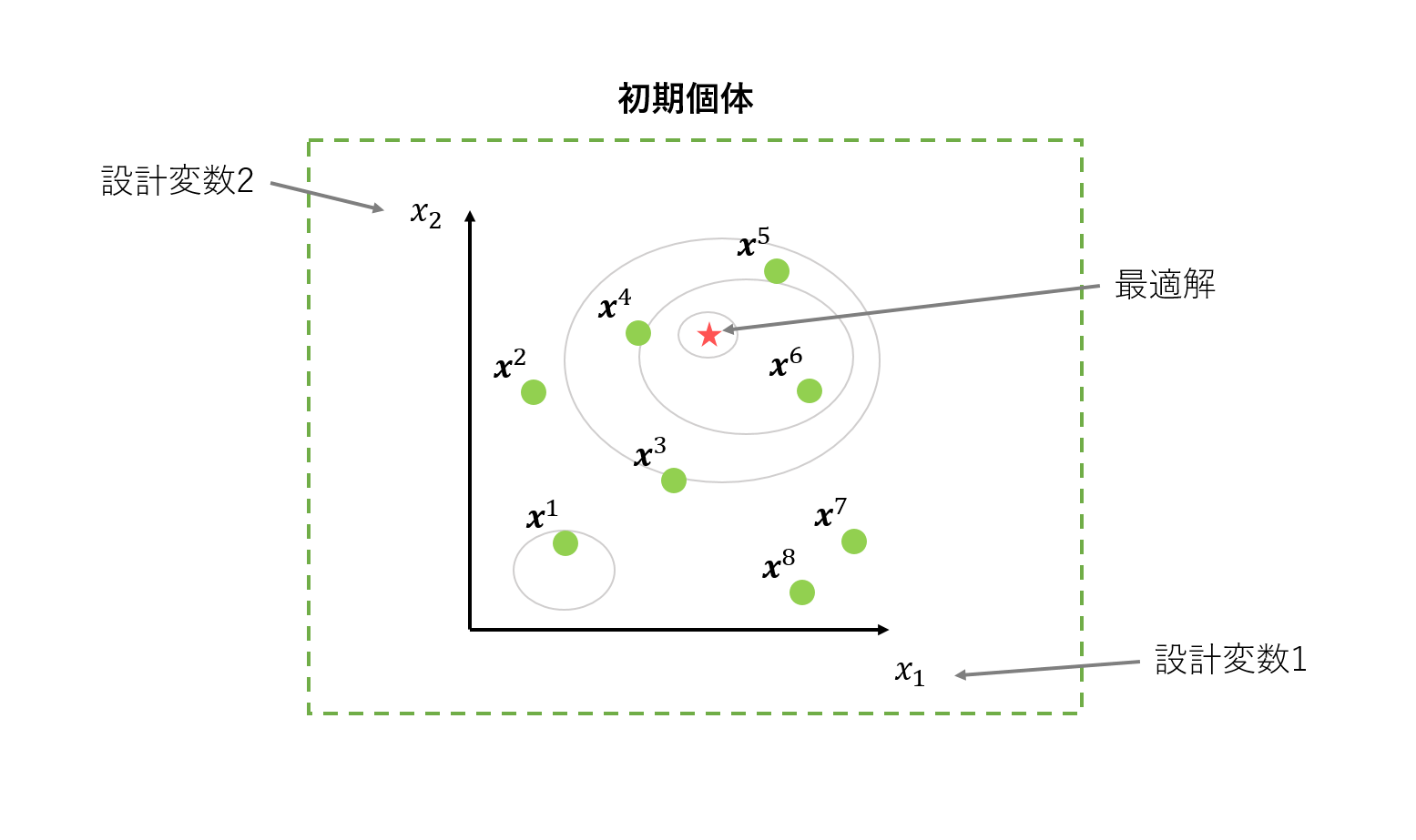
初期個体（緑の丸）をランダムに生成します。今回の例では、変数を2つ持つ問題の最適化をします。要は緑の丸をいい感じに動かして、赤い星の位置を探すだけです。

2. 交叉・突然変異

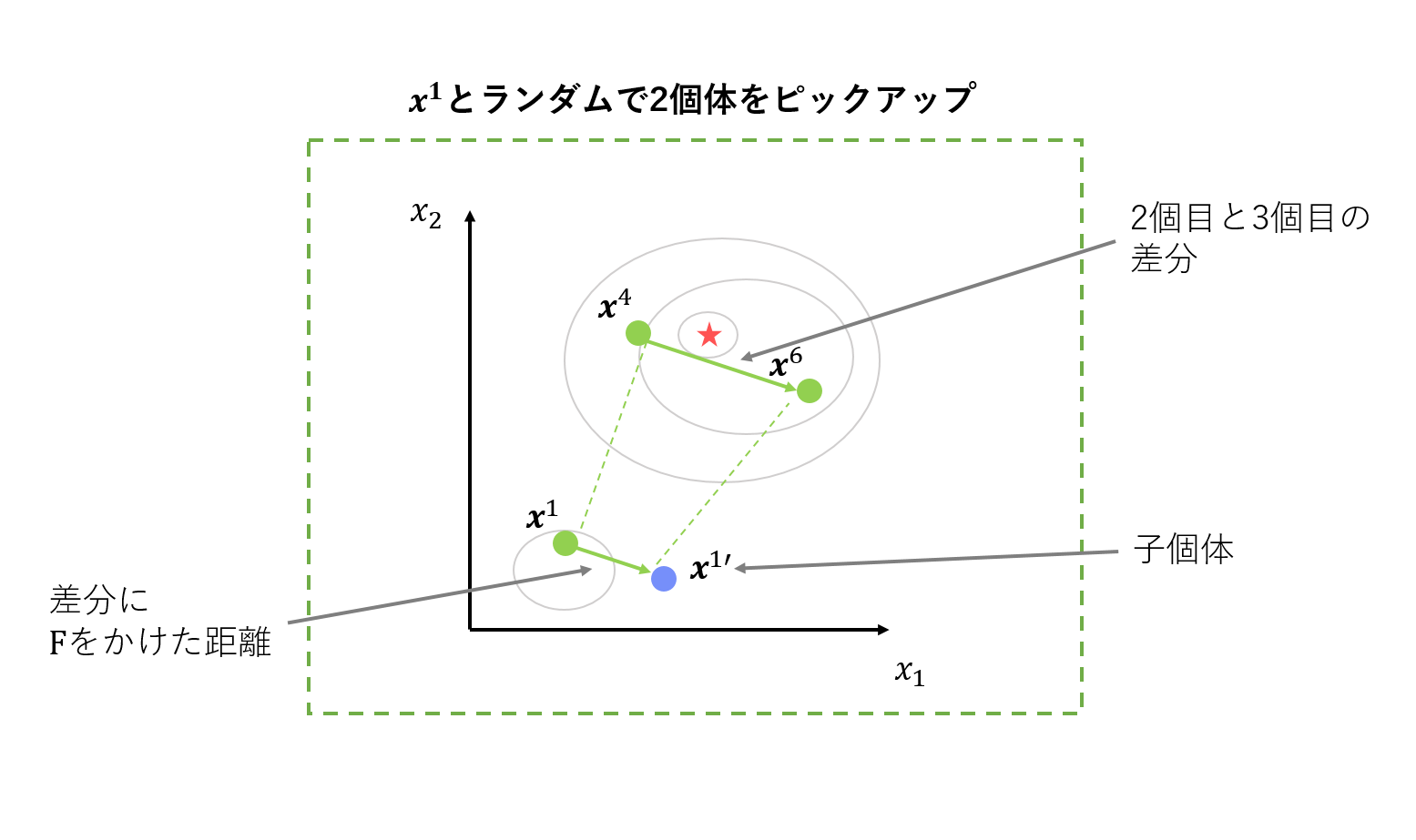
親個体をいくつか選び、組み合わせて子個体を生成します。具体的には、ある親個体（この場合$\boldsymbol{x}^1$）に、ランダムに選択した二つの個体の差分にスケーリングパラメータ$F$をかけたものを足します。

$F$は、その名の通り探索のスケーリングをするハイパーパラメータです。$F$の値が大きいと、大ぶりな探索になります。探索は早いですが、あっちにいったりこっちにいったりで収束しない可能性があります。$F$の値が小さいと、細かい探索になります。移動距離が短くなるため、局所解からなかなか抜け出せない可能性があります。このように、適切な値を設定しないと探索がうまくいかない、超重要なパラメータです。一般的には、0.5に設定されることが多い気がします。

ここでの個体の選び方にはいくつか種類がありますが、詳細は割愛します。
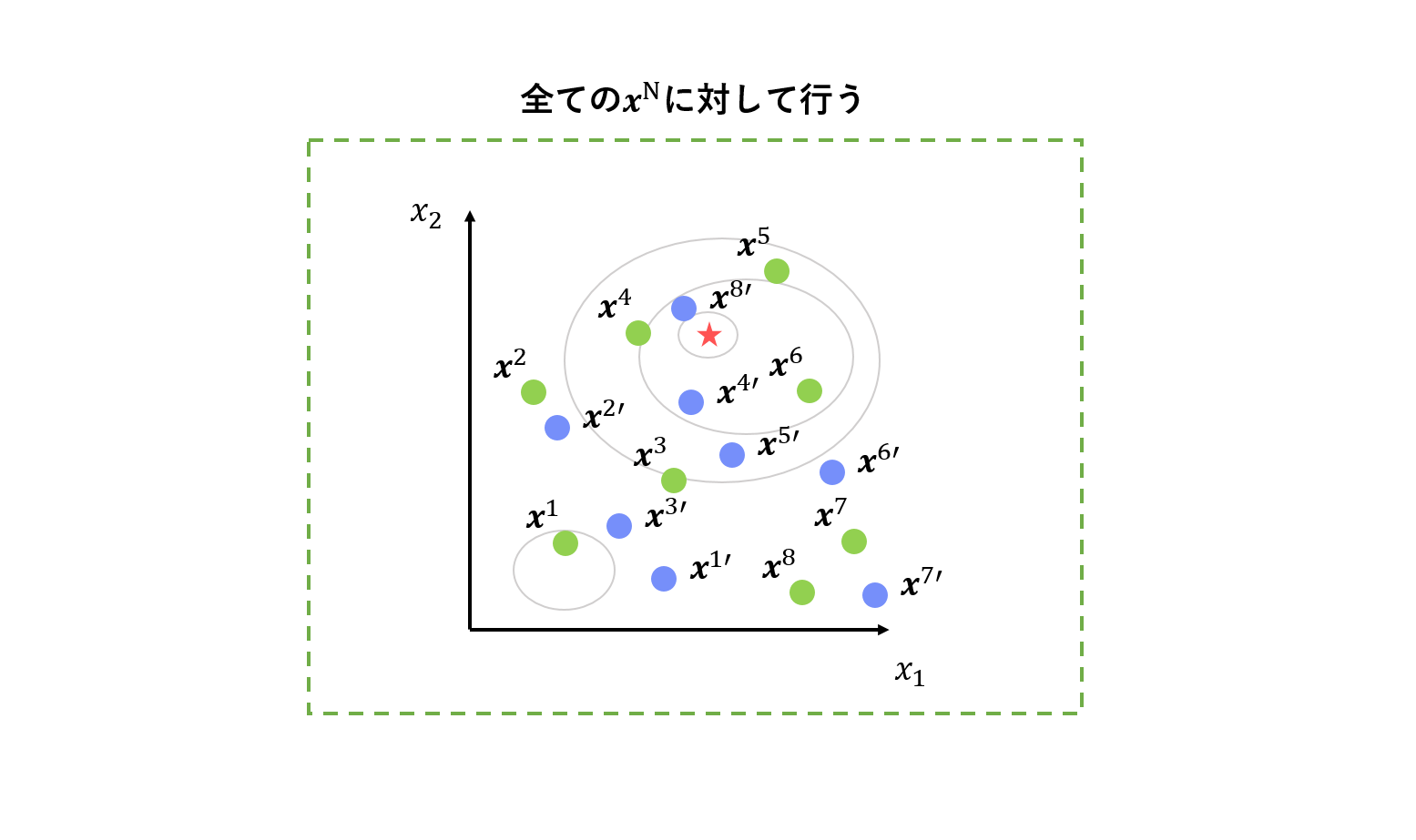
この操作を全ての個体に対して行います。

余談ですが、代表的なDEの交叉方法に「binomial交叉」「exponential交叉」があります。しかし、exponential交叉は「設計変数が隣り合っている」という情報を使用してしまっており、依存関係を持つ変数が隣り合っている問題に対して不適切に高い性能を示してしまうため、binomial交叉を使用することを推奨します。

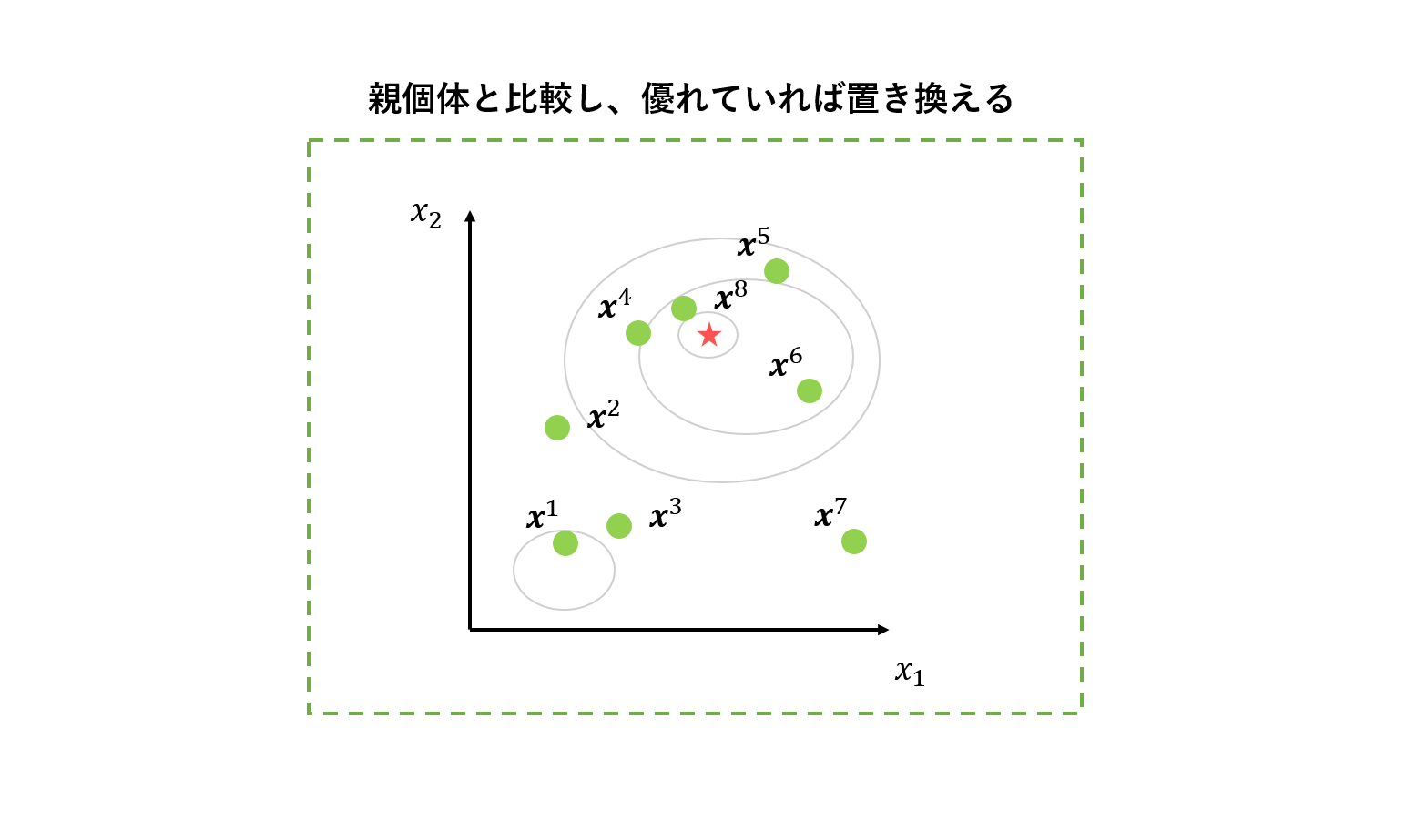
3. 選択

親個体と子個体を比較し、優れている方を残します。

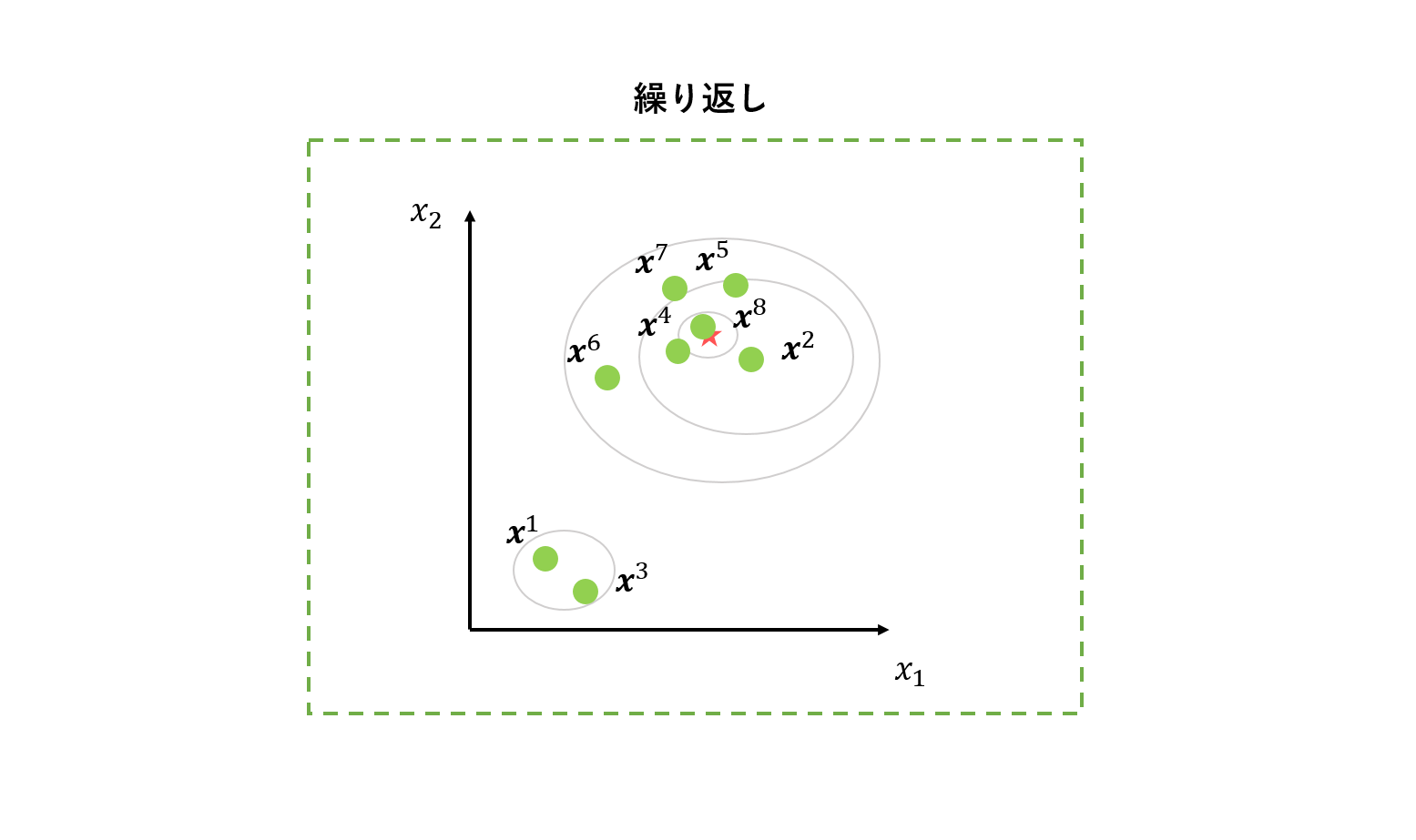
4. 繰り返し

2~3を繰り返します。これらを繰り返すことで、良質な個体を次世代に残し、探索を進めていきます。

ここでポイントなのは、探索が進むにつれて個体群は似通った箇所に集まってくるということです。こうなることで、2で選択する個体は、探索終盤では必然的に距離の近い個体が選ばれやすくなります。つまり、探索序盤は大きく移動することで大域的探索を、探索終盤は細かく移動することで有望領域の集中的な探査を「自動的に」するようになっています。

DEの改良版

DEは進化型多目的最適化アルゴリズムの遺伝的操作としてもよく使われているほか、DEの改良アルゴリズムはいくつも提案されています。その中で有名っぽいものをいくつかコンセプトだけ紹介します。

JADE³

パラメータ適応型DEです。DEのハイパーパラメータであるスケーリングパラメータ$F$、交叉率$C$を探索中に適応的に調節し、事前設定不要にしてしまおう、というアルゴリズムです。基本的には、解更新に成功した時のハイパーパラメータの値を次世代でも使おうぜ、という思想のもと調節していきます。

ただし、DEの性質上、本来は適していないはずのハイパーパラメータで「たまたま」解更新に成功する場合も当然あり得ます。JADEの場合、その「たまたま」が母集団全体に影響してしまうため、間違った方向性で探索が進んでしまうケースがあり得ます。

SHADE⁴

SHADEは、「解更新に成功した時のハイパーパラメータの値を次世代でも使う」という設計思想はJADEと同様ですが、解更新に成功したパラメータを保存する長さ$H$のメモリを持っているところが異なります。そして、解更新に成功した場合、そのメモリの要素のうち、ひとつだけを更新します。これにより、「たまたま」うまく行ったパラメータの次世代への影響を抑えることができ、高い探索性能を誇っています。

おわりに

ここまで書いてあれですが、そもそも進化計算自体が今はあまり流行っていないですよね・・・。知る限り、最近では最適なニューラルネットワークの構造を進化計算で解く「ニューロエボリューション」の枠組みでCMA-ESが使われているくらいです。個人的に好きな分野なので、他に事例を知っている方がいれば、是非教えてください！！

R. Storn and K. Price. Differential Evolution - A simple and efficient adaptive scheme for global optimization over continuous spaces. Technical report, International Computer Science Institute, Berkeley, CA, 1995. ↩
R. Storn and K. Price. Differential Evolution - A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Global Optimiz., 11(4):341–359,1997. ↩
J. Zhang and A. C. Sanderson. JADE: Adaptive Differential Evolution With Optional External Archive. IEEE Tran. Evol. Comput., 13(5):945–958, 2009. ↩
R. Tanabe and A. Fukunaga, "Success-history based parameter adaptation for Differential Evolution," 2013 IEEE Congress on Evolutionary Computation, Cancun, 2013, pp. 71-78. ↩

差分進化（Differential Evolution, DE）とその改良手法