つぶやき:久しぶりに読み返してみた.途中まで悪くなかったのに,後半ものすごく未熟さが滲み出てる.お恥ずかしい...
しかもなんかパーサーの仕様変わったとかで所々表示バグってますね.簡単に直せるとこだけ直しました.
0. はじめに
こちらは,1ヶ月前まで強化学習に関する知識が完全にゼロ(2ヶ月前までは機械学習の知識がほぼゼロ)だった大学3年生の筆者が,ちょっとしたゲームAIを手探りで作ってみた記録,そんなレベルの記事です.未熟者の私ですが,
- 自分の理解を整理・確認する
- 至らない点を知識のある方々に補っていただく
- 強化学習について何も知らないけど興味はある.でも手元に特に教材がない.という方へのチュートリアルになればいいな
あたりを目的としてこの記事の執筆に至りました.興味があれば暖かく読んでいただけると嬉しいです.コメント等によるご指摘も歓迎いたします.
0-1. 参考文献
筆者が強化学習を学ぶにあたり,「ITエンジニアのための強化学習理論入門」(中井悦司) という書籍をまず教科書として購入し,べたべた読ませていただきました.執筆にあたってもこの上なくお世話になりましたので,この場で紹介させていただきます.
また,記事に載せたソースコードのうち,一部この本に掲載されていたものと非常に似通った部分があることをお断りしておきます.ご了承ください.
それから筆者は,強化学習を学ぶ前に「Pythonではじめる機械学習入門」「ゼロから作るDeepLearning」(ともにオライリー・ジャパン)の2冊を読んで機械学習・深層学習についてある程度オベンキョしましたのでこれも載せておきます.特に後者は,AI実装パートの理解に役立つ部分があるかと思います.
0-2. 記事の大まかな流れ
この記事ではまずAIに習得させるゲームの紹介および目標の設定を行います.次に強化学習および今回用いるDQNアルゴリズムに関する理論的なお話を整理して,最後にソースコードの晒しあげと学習結果の確認,そこで浮かんだ問題点・改善案の列挙,という流れにしようと思います.興味のあるパートだけでも覗いてくださると嬉しいです.
追記.書き上げてみたところ,理論編が予想以上にヘビーになりました.筆者のように理論屋的な性格の方は,べたべたすると楽しいかもしれません.そんなモチベのない方は,程々になぞるくらいにとどめておく方がいいかもしれません.
0-3. 使用する言語
Pythonさんのお力を借ります.筆者は jupyter notebook で実行しております.(おそらく盤面の可視化関数以外はその他の環境でも動きますが,確認はしていません.可視化関数は大したものではないので,そんなに気にしなくてもいいです.)
またクライマックスで,ディープラーニングのフレームワーク「TensorFlow」をちょこっと使います.最後までコードを実行したい!という方は,該当箇所の実行にはインストールが必要ですのでそこだけお願いします.またここではGPUが利用できると高速に処理できるのですが,筆者にはそんな環境も知識もないため,CPU(普通の)でゴリ押しました.Google Colab などを使えばGPUが無償で利用できますが,セッション切れでの事故が嫌すぎて回避しました.このあたりの判断はお任せします.
0-4. 前提知識
記事を読んで雰囲気を掴むだけなら,特別な知識はほぼ不要です.
理論編をきちんと理解するには,高校数学(確率,漸化式くらい)のある程度の理解が,実装編をストレスなく読むには,Pythonの基本文法がわかっていれば十分かと思います(クラスの概念について不安がある方は,軽く見直すとよいです).また,アルゴリズム(動的計画法など)の事前知識があると,理解がしやすくなると思います.
ただ一点,ニューラルネットワークに関してだけは,本記事で解説を行わないかつ,知識があるとないとで結構変わってくる分野かと思います.「こういうものだと思ってください」的な宣言はするので鵜呑みにしてもらえれば理解に支障はないと思いますが,きちんと知りたい方は別個にオベンキョすることを勧めます.
それでは本編行きます!!
1. 取り扱うゲームの紹介
学習のテーマとして選んだのは2048ゲームです(↓こういうの).ご存知でしょうか?
このあとルールを説明しますが,非常に簡単なのでやってみればわかると思います.スマホアプリでもWeb版でもいくらでもあるので,ぜひ遊んでみてください.
1-1. ルール
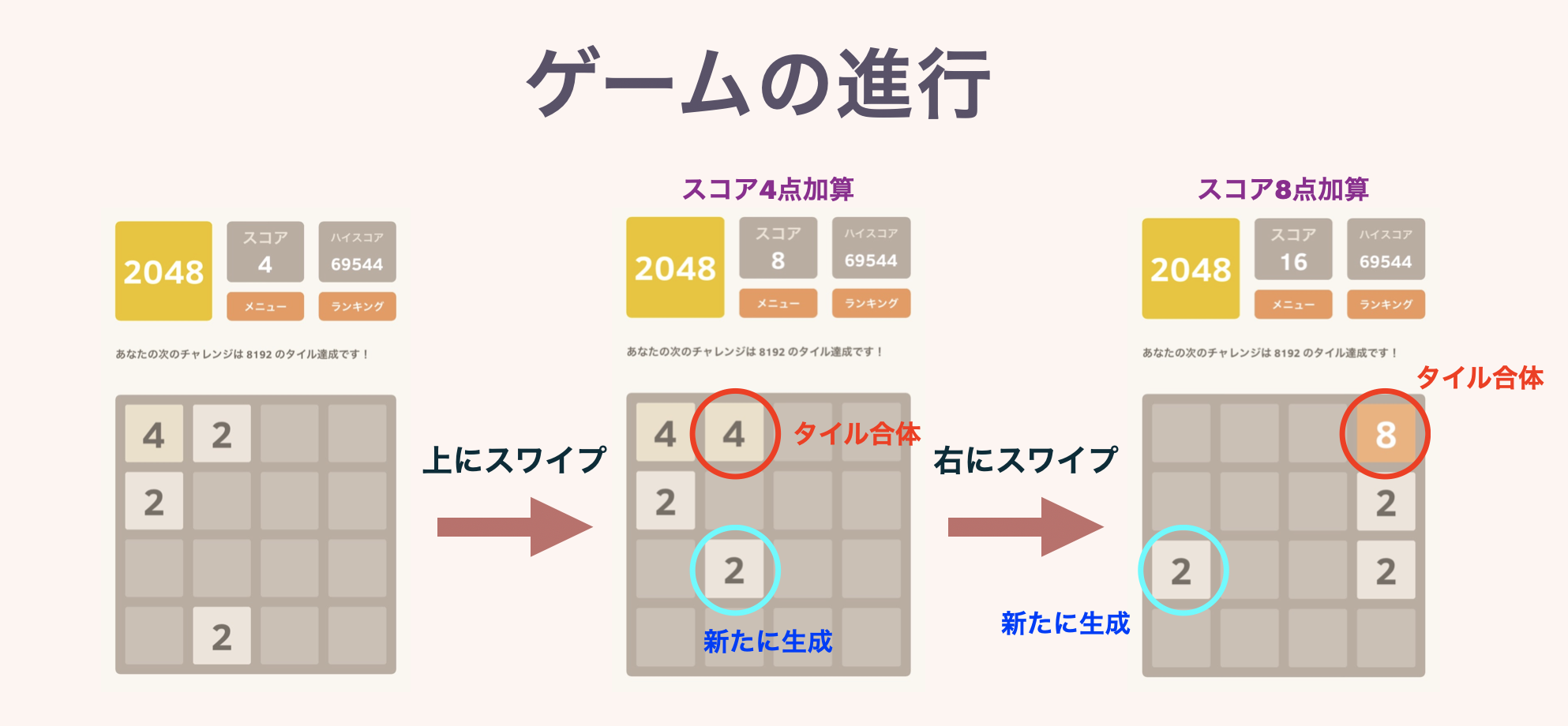
4$\times$4マスの盤面に,2の累乗の数字が書かれたタイルが置かれています.ゲーム開始時はランダムに選ばれた2マスに,「2」または「4」のタイルが置かれています.
プレイヤーは毎ターンごとに,上下左右4方向のうちひとつ選んで,スワイプするなりボタンを押すなりします.すると,その方向に向かって盤上全てのタイルが滑ります.この際,同じ数字のタイルがぶつかると,合体して数字が大きくなり,1枚のタイルになります.またこのとき,できたタイルに書かれている数字が,スコアとして加算されていきます.
毎ターン終了時に,空いているマスのどこかひとつに,「2」または「4」のタイルが新しく生成されます.どの方向にも動かせなくなったらゲームオーバー.それまでにハイスコアを目指しましょう!というゲームです.一応このゲームの名前通り,はじめは「2048のタイルを作る」ことが目標として設定されています.
↓図解です.本当にルールは簡単です.
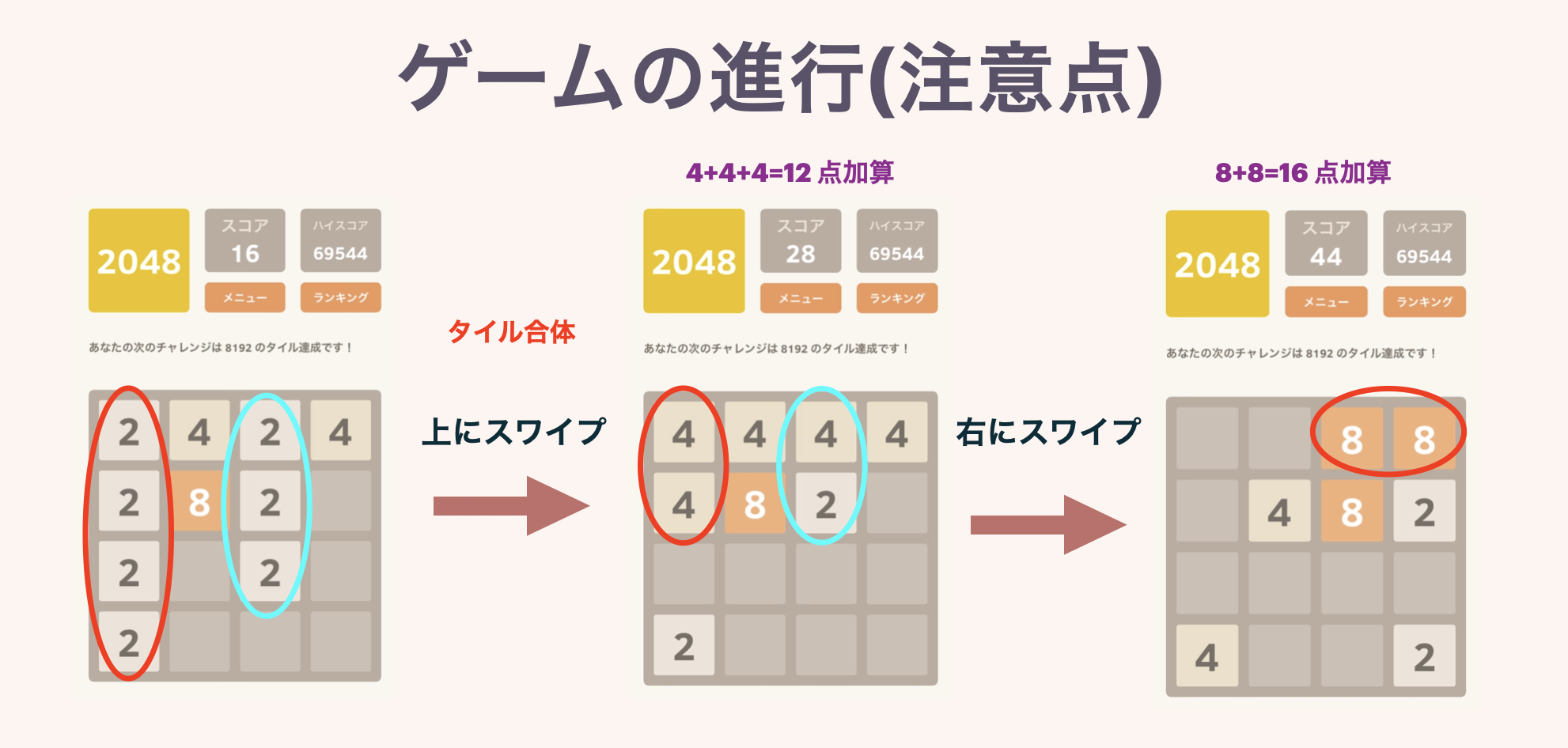
2つ目の図で同じ数字のタイルが3枚以上並んでいる場合の挙動を示しています.また複数枚のタイルが同時に完成した場合は,きちんとその分のスコアが加算されます.

1-2. このゲームのコツ
このゲームには運要素もある程度ありますが,スコアにはプレイヤーの練度が多分に反映されます.つまりは「勉強・練習によって上手くなれるゲーム」です.のちにAIくんにゲームの練習をしてもらうわけですが,このタイミングで筆者が掴んだこのゲームのコツを軽く書いておこうと思います.もしAIくんがこのコツを自分で学習することができれば偉いですね.
ただ,「どのくらいのレベルのAIが作れるのかを体感したい!」という方は,**このコツを見ないで何回かプレイしてみることを勧めます.**自分のはじめの実力がどのくらいのスコアなのか,を知っておくと,今後のAIの学習過程で,今どのレベルなのか,というのが少しわかりやすいと思います.(まあ別にいいやという方は,普通にオープンしちゃっても構いません.)
以上を了解したうえで,この中身を読んでください(左の三角マークをクリック).
このゲーム,最初のうちはどう動かしてもどこかでタイルが合体するのでよいのですが,そのうち大きい数字が邪魔になってきて,どんどん盤面が狭くなってしまいます.そこで,「どこかの角に大きい数字を集める」という方針をとるのが非常に有効です.(どうすれば角に集められるのか,というのはまた色々コツがあるんですが.)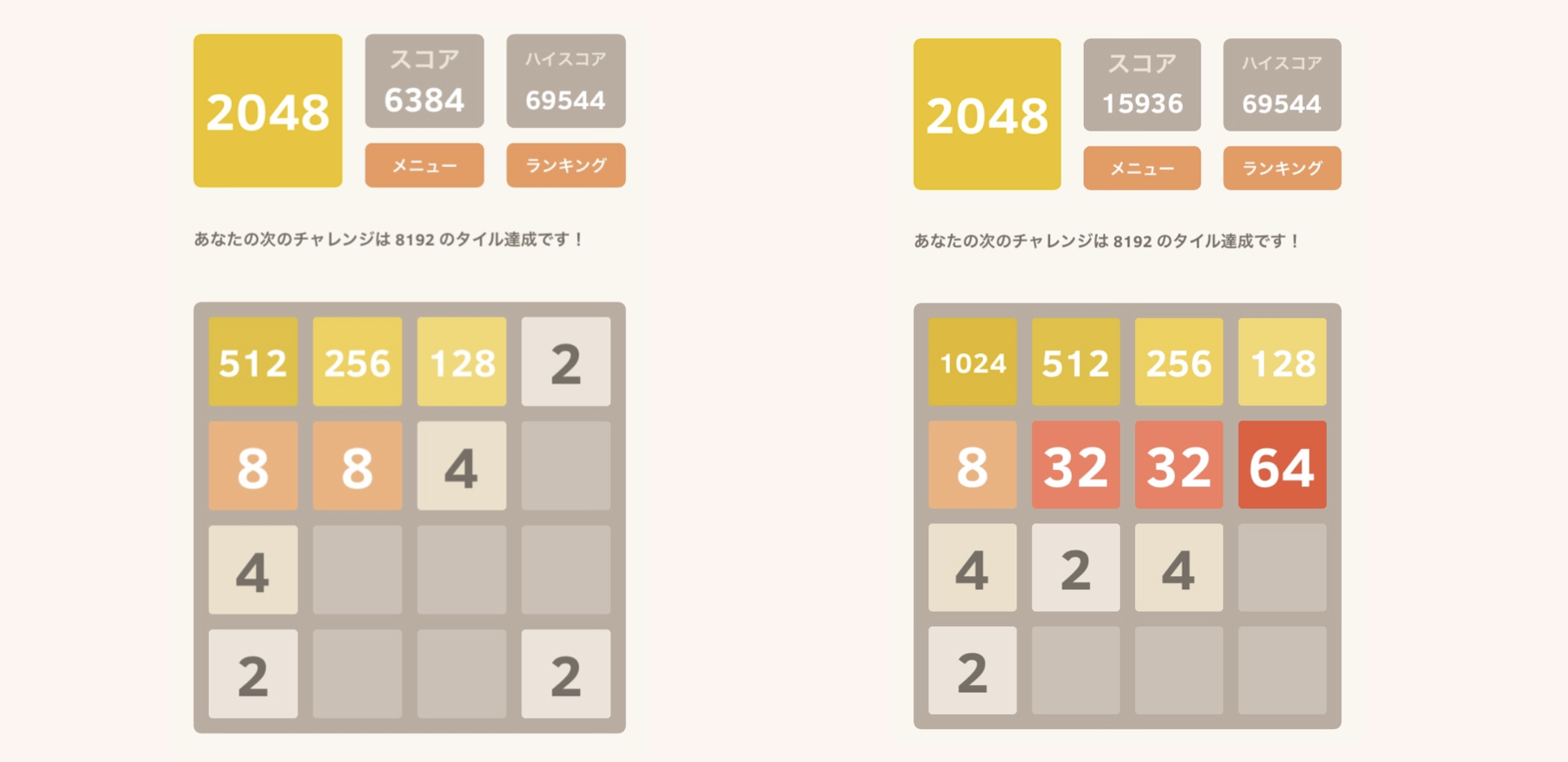
左の図では,左上方面に大きい数字を集めています.この盤面で,下にスワイプなどをしてしまうと,「256」や「128」が真ん中の方で邪魔なタイルになってしまい,一気に不安定になってしまいます(本当に一気にゲームオーバーまで行きます).
この形を崩さないように丁寧にプレイしていくと,右の図のような盤面まで持ち込めます.ここからなら「2048」まで一直線で行けることがわかるでしょう.一気にタイルを集める瞬間は,このゲームで一番の快感ポイントです.
1-3. 目標
一応ですが今回の目標(夢)を立てておきます.理想は「自分より高スコアを取れるAI」です.私はこのゲームをそれなりに理解しているつもりで,先ほどチラ見せしたスクショでのハイスコア69544点というのは相当高めなのですが,もしこれをAIくんが超えてきたら感動します.
スコアの目安ですが,このゲームを知らない人間が初見プレイをすると,だいたい1000~3000点くらいでゲームオーバーとなります.何回かプレイしてゲームに慣れてくると,5000~7000点くらい出せるようになります.(私の周りの人間ではこんな傾向だった,というだけです.サンプルも少ないので参考程度でお願いします).またのちに述べますが,完全ランダムに手を選ぶと,平均で1000点くらいしか取れません.
では,2048ゲームの話はこれくらいにして,本題の強化学習に入りましょう!
2. 理論武装
実装に先立って,今回のゲームAI作成のベースにある理論をかいつまんで割としっかりと整理します.強化学習の基礎的なところから,今回用いたDQNに至るまでの流れを辿れればいいかなと思っています.筆者もオベンキョしながら一歩ずつ書き進めるので一緒に頑張りましょう.
2-1. 強化学習について
そもそも強化学習とは,教師あり学習・教師なし学習あたりと並ぶ,機械学習のあるひとつの分野です.何らかの環境を動き回るエージェントを定義し,データの収集を繰り返すなかで学習処理を進め,得られる"報酬"を最大化するような最適な行動を学習していく,というのが強化学習の流れです.よく聞く将棋や囲碁のAI,自動運転技術などで,強化学習が応用されているそうです.
以下では2048ゲームをテーマに据えながら,もう少し専門用語も取り入れて整理していこうと思います.
2-1-1. 行動ポリシー
強化学習を始めるにあたっては,まず実際にゲームをプレイする「エージェント」を定義します(今回の実装でエージェントそのものを定義したかと言われると微妙なのですが,仮想的にでもゲームをプレイする存在を意識しておくといい気がします).また,ゲーム内に「報酬」を設定して,エージェントに「ゲーム終了時の報酬を最大化する」という目的を持たせます.報酬の設定の仕方は重要な要素です.また,プレイの中で,エージェントは様々な盤面に遭遇し,そこでとる「行動(アクション)」の選択に迫られます.それぞれの盤面のことを,強化学習的な用語では「状態」と呼びます.
エージェントの学習が完了した,というのは,究極的には「すべての状態sに対して,最善のアクションaがわかっている」ということです.例として「○×ゲーム」を考えるとわかりやすいです.あのゲームは,両者が最善手を打ち続ける限りかならず引き分けになります.ということは,発生しうるすべての状態(盤面)に対してそれを「暗記」しておけば,極論ルールすら知らなくても,その人は不敗の○×ゲームマスターとなります.
ここで「行動ポリシー」という用語を定義します.これは,「各状態に対してエージェントがアクションを選択するルール」のことです.行動ポリシーを固定したエージェントは,まるで機械のように(まあ機械なんですが)一定のルールに従って次の手を選択しゲームをプレイします.強化学習の目的は,この行動ポリシーを最適化すること,最適な行動ポリシーを求めること,と言い換えてもいいかもしれません.○×ゲームの例では,暗記すべきだった最善手たちに従うことが,最適な行動ポリシーにあたります.
なお,行動ポリシーは記号 $\pi$ で表すのが慣例らしいです.
2-1-2. 状態価値関数
さっきから学習学習いってますが,具体的にどう学習するんだ,という話を始めます.
まず,状態価値関数 $v_\pi(s)$ を定義します.これは特定の行動ポリシーπを前提とし,状態sを引数にとる関数です.返り値は「状態sからスタートし,ゲーム終了まで行動ポリシーπに従ってアクションを選択し続けたとき,現在以降に得られる報酬の合計の期待値」です.
?となるかもしれませんが,よく考えれば大したことはないです.行動ポリシーを固定したとき,状態価値関数の値は,「各盤面がどれくらい良い盤面か」を表します.
数式を使った方が(個人的には)気持ちがよくわかるのでそれも示します.いきなり出てきた記号はすべて意味を述べます.
$$
v_\pi(s) = \sum_{a}\left( \pi(a\ |\ s)\sum_{(r,s')} p(r,s'\ |\ s,a) \left( r+v_\pi(s') \right) \right)\tag{1}
$$
はいこれが状態価値関数が一般に満たす等式です.これをベルマン方程式と呼ぶそうです.
- $p(r,s'\ |\ s,a)$ は,「状態sからアクションaを選択したときに,報酬としてrが得られ,かつ状態s'に遷移する条件付き確率」を表します.(同じ盤面で同じアクションを選択したとしても,つねに同じ報酬・遷移先が得られるとは限らないためこの措置がとられています.例えば2048ゲームでは,新たに生成されるタイルの位置がランダムです.)
- $r+v_\pi(s')$ は,「はじめの1アクションでaを選択したら報酬rを獲得して状態s'に遷移し,その後はゲーム終了まで行動ポリシーπに従った場合に,今から得られる報酬の和の期待値」を表します.
- $\pi(a\ |\ s)$ は,「行動ポリシーπにおいて,状態sのときアクションaが選択される条件付き確率」を表します.(πが確率的なアクション選択を含まない場合は,ここは削ることができます.)
以上をまとめると,内側のシグマでは「現状態sからアクションaを選択し,その後はずっとπに従って行動した場合に,今から得られる報酬の和の期待値」が表現されています.さらに,外のシグマでアクションに関して和をとることで,「現状態sから行動ポリシーπに従ってアクションを選択し続けた場合に,ゲーム終了までに得られる報酬の合計の期待値」となるわけです.
補足 「割引率」について
(1)のベルマン方程式では,一般には「割引率」というパラメータが導入されます(記号はγ).しかし今回は,実装パートで $\gamma=1$ としたために結局(1)と等価な式になることと,筆者の理解度が浅いことを理由に扱わないことにしました.ごめんなさい.上の(1)式は,状態価値関数の定義というより計算法を示しています.ただ一点,終了状態(ゲームオーバー盤面)に対する状態価値関数の値を0と事前に定義しておけば,そこから前の状態,前の状態,と遡っていくことですべての状態について状態価値関数の値を計算することができます.正しい状態価値関数の値が,終了状態から徐々に伝播していくイメージです.高校数学で言えば漸化式,アルゴリズムで言えば動的計画法の考え方になります.
動的計画法についてこれ以上深追いはしません.ただ,この計算を行うには,少なくとも全状態についてのループを回す必要があるということは心に留めておくといいかもしれません.
さて,状態価値関数を定義自体はしましたが,結局「学習」というのは何をするのかがまだ示されていません.次でその問いに答えようと思います.
2-1-3. 行動-状態価値関数
先に述べた状態価値関数は,行動ポリシーπが定まっているという前提のもとで,各状態が良いか悪いかを判定するものです.つまり,それ単体では行動ポリシーπを改善することができません.ここでは,より良い行動ポリシーをどう得るかを説明します.ただしここで,行動ポリシーが「より良い」というのは,
「任意の状態sに対して,$v_{\pi1}(s)\leq v_{\pi2}(s)$ が成り立つこと」
であると定めます.(π1よりも,π2の方が「良い」行動ポリシーです.)
非常に名前が似ていますが,行動-状態価値関数 $q_\pi(s,a)$ を定義します.これは,「現状態sからアクションaを選択して,その後はずっと行動ポリシーπに従ってアクションを選び続けた場合,今から得られる総報酬の期待値」を表します.あれ?と思った方もいるかと思いますが,これは(1)式の一部にまるまる登場します.すなわち,
$$
q_\pi(s,a) = \sum_{(r,s')} p(r,s'\ |\ s,a) \left( r+v_\pi(s')\right) \tag{2}
$$
です.これを用いると,(1)式は
$$
v_{\pi}(s) = \sum_{a} \pi(a\ |\ s)q_{\pi}(s,a) \tag{3}
$$
と表現することができます.
さて一気に結論を述べます.行動ポリシーを改善する方法は,「現状態sにおいて選択できるすべてのアクションaについて,行動-状態価値関数 $q_{\pi}(s,a)$ の値を参照し,これが最大となるアクションaを選ぶよう,行動ポリシーを修正する」 です.
これはつまるところ,「1手だけ現状の行動ポリシーを無視して違う世界を見て,一番よさそうな手を選ぶようにポリシーを修正する」ということです.この改善をひたすら続けていけば,「より良い」ポリシーがどんどん得られていくことは直感的にもわかるのでは,と思います.これは一応数式的に示すことも可能ですが,割と面倒なのでここでは割愛します.
2-1-4. ここまでのまとめ
色々言ってきましたが,とりあえず整理が一段落したので簡潔にまとめておきます.エージェントが最適な行動ポリシーを学習するまでの流れは,
- とりあえず適当に行動ポリシー $\pi$ を設定する.
- 状態価値関数 $v_{\pi}(s)$ を動的計画法で計算する.
- 行動-状態価値関数 $q_{\pi}(s,a)$ を,式(2)で計算する.
- 新たな行動ポリシー $\pi'$ を,上で説明した方法で作成する.
- この $\pi'$ をはじめの行動ポリシーπと置き換えて,同じ操作を繰り返す.
です.これをひたすら繰り返すことで,エージェントはどんどん優れた行動ポリシーを得ることができます.これが,強化学習における「学習」の仕組みです.
補足 ちょっとだけごまかしたポイントについて
上のループをひたすら繰り返せば理論上学習ができる的な話をしましたが,実際に計算をしようとすると,(1)や(2)に現れる $p(r,s'\ |\ s,a)$ の値がわかるのか,という問題に直面します.ゲームの仕様を(私たちプログラマが)完全に理解していて理論的に求められるならばそれでいいですが,未知のゲームをプレイするときはここがわからない場合も考えられます. これについては,のちに2-2-3. TD法 で回収しようと思います.
2-2. Q-Learning
上でまとめたアルゴリズムは,紛れもなく正しい学習アルゴリズムではあるのですが,ポリシーの改善は1ゲーム終了まで行われず,さらに「現状の行動ポリシーではゲーム終了までこぎつけられるとは限らない」という欠点があります.2048ゲームに関してはそんなことはないのですが,一般のゲームに適用する際(たとえば迷路など)にはここが大きな問題となります.この点を解決したのがQ-Learningのアルゴリズムであり,今回こちらを実装したので以下で解説します.
2-2-1. オフポリシー
ここでは用語の定義だけします.我々はあくまで行動ポリシーの改善を目的としているわけですが,よく考えてみると,エージェントがプレイしてデータを収集する際は,別に現状の最適な行動ポリシーに従ってデータを集める必要はありません.そこで,「改善対象のポリシーとは異なるポリシーに従ってエージェントを動かし,データを収集する」手法について考えます.これをオフポリシーでのデータ収集と呼ぶことにします.
2-2-2. Greedyポリシー
若干今更感がありますが,Greedyポリシーという語を定義します.これは,「確率的な要素を持たず,アクションを選択し続けるような行動ポリシー」のことです.(1)式や(3)式に登場させた条件付き確率 $\pi(a\ |\ s)$ が,ある特定のaについてのみ1,それ以外のアクションについては0となるようなポリシーだと言い換えることもできます.
Greedyポリシーπにおいては,状態sを定めればアクションも1つに確定するので,そのアクションのことを $\pi(s)$ と表現することにします.
このとき一般に,
$$
v_{\pi}(s') = q_{\pi}(s', \pi(s')) \tag{4}
$$というように,状態価値関数を行動-状態価値関数を用いて表すことができます.sではなくs'としたのは形式を合わせるためで,これを(2)式に代入することで,
$$
q_\pi(s,a) = \sum_{(r,s')} p(r,s'\ |\ s,a) \left( r+q_{\pi}(s',\pi(s'))\right) \tag{5}
$$
という等式が得られます.これは行動-状態価値関数に対するベルマン方程式と呼ばれています.この式により左辺の値は,状態sでアクションaを選択したときの報酬rおよび遷移先の状態s',$q_{\pi}(s',\pi(s'))$ を用いて計算し直すことができます.またこの式ならば,状態価値関数を経由する必要がありません.
次で(5)式を生かしたQ-Learningの概要を示します.
2-2-3. TD法
はじめに説明したアルゴリズムでは,1ゲームの終了を待たないと,ポリシーの改善が行えないと述べました.これに対し,1ターン分のデータを収集した瞬間に,更新処理を行う手法が存在します.これが「TD法(Temporal-Difference法)」と呼ばれるもので,オフポリシーでデータ収集して行うTD法のことを,Q-Learningと呼びます.これならデータ収集中にもAIくんは賢くなれるため,永遠に迷路のゴールにたどり着けない,という事態を回避できます.
更新は式(5)を用いて行います.$p(r,s'\ |\ s,a)$ の値をはじめは未知とし,得られたデータから近似値を計算,さらにデータを集めることでどんどん真の値に近づけていきます.これと同時に行動-状態価値関数の値も修正されていく,という仕組みです.
ただ実際のQ-Learningでは,(5)式ではなく以下の式で値の修正を行うそうです.(行動-状態価値関数の値を $r+q_{\pi}(s',\pi(s'))$ に近づける,という気持ちはそのままです.)
$$
q_{\pi}(s,a) \longrightarrow q_{\pi}(s,a)+ \alpha \left\{ r+q_{\pi}(s',\pi(s') - q_{\pi}(s,a)) \right\} \tag{6}
$$
αは修正の重みを調節するパラメータで,学習率とか呼ぶそうです.(これは完全に私の予想ですが,すべての(s,a)の組に対し $p(r,s'\ |\ s,a)$ の値を保持・更新していくというのはメモリ的に厳しい場合が多いのではないでしょうか.)
はい.最後の方少し雑に説明してしまいましたが,正直に言うと実装パートではこの式を使わないので少しモチベが下がってました.とにかく重要なのは,オフポリシーでデータを集めながら行動-状態価値関数の更新を行っていき,この値を最大化するアクションを選ぶことでより良い行動ポリシーが得られる,という考え方です.これに基づいた本番用のアルゴリズムの仕組みを次で示し,長かった理論編を締めます.
2-3. DQN
理論編では,まず強化学習の基本的な仕組みを説明し,それを効率化するQ-Learningという手法を述べました.しかし現状のアルゴリズムでは致命的な問題が残っています.それは,「とりうる状態の数が多すぎる場合に,学習処理が終わらない」という点です.
これまでのアルゴリズムでは,どんなに少なく見積もっても,あり得る状態の数だけ計算を行い,全状態に対して行動-状態価値関数の値を求めなければなりません(もちろんこれを何周も何周もして,より良いポリシーを得ることになります).Pythonが1秒間に行える演算の量はせいぜい $10^{7}$ 回だとかそこいらなのに対し,2048ゲームにおける状態の数は,まあ盤面に16マスありますし $12^{16}$ くらいはありそうですよね.この長さのループを何周もする...と考えると,学習は到底終わらなそうです.将棋や囲碁の状態数とか言い始めたらそれこそ永遠に終わりません.(Pythonの演算速度について私はそんなに詳しくないのでザックリ書きましたが,まあとりあえず終わりません.)
この問題を解決するため,偉大なニューラルネットワークさんを持ち出してきて,Q-Learningをしてやろう,というのがDQNです.DQNは Deep Q Network の頭文字です.
2-3-1. ニューラルネットワーク
改めてですが,ニューラルネットワークの詳しい理論・仕組みに関してはこの記事では追いません.ここでは,2048ゲームAIくんの学習の仕組みを理解するために,最低限必要な世界観を述べます.(というか私も未熟者なので深いことはわからないんですごめんなさい.)
ニューラルネットワークは,深層学習(ディープラーニング) で用いられるものなのですが,本当に平たく言ってしまうとこれは「関数」です.(多変数入力,多変数出力がデフォです).単純な一次関数を多数用意し,入力をそれに通し,チョチョっと処理を加える.この操作を何層にも重ねたのちに,何らかの形で出力がされる.というのがニューラルネットワークです.内部の関数の数や処理の種類,層の数をいじることで,本当に柔軟に,いろんな関数に化けることができます.(以下,ニューラルネットワークのことをたまに「NN」と略します.)
そしてニューラルネットワークにはもう一つ重要な機能があります.それがパラメータのチューニングです.先ほどはNNの中身を固定して関数として働くというものでしたが,入力と同時に「正解」の出力をNNに与えることで,正解に近い値を出力するよう,内部関数に含まれるパラメータの値を修正することができます.望みの性質を持つ関数になるように,ニューラルネットワークは「学習」ができるということです.
実装にあたっては,今回はフレームワークTensorFlowの力を借りるので,中身の理解はこのくらいでもとりあえず大丈夫かと思います.オベンキョはまたの機会に.
2-3-2. 畳み込みニューラルネットワーク(CNN)
畳み込みニューラルネットワークと呼ばれる種類のNNがあります.これは画像認識等に用いられている類のもので,シンプルに入力値を与えるよりも,入力の2次元的な広がり(ちょうど盤面のような)の特徴をつかむのに優れています.ので今回使います.とりあえずそれだけ.
2-3-3. Q-Learningに組み込む
NNをどう使うかというと,「盤面の状態とアクションから行動-状態価値関数の値を計算するニューラルネットワークを作る」です.全状態・アクションについて $q_{\pi}(s,a)$ を求めていくという従来の方法は無理ぽという話でしたが,このようなNNが作れれば,「何となく似ている」「通ずる部分がある」ような盤面を見て,最善と思われるような手を選ぶことができるようになると期待できます.
式で理解します.(5)式(6)式あたりと同様,Q-Learningでは $q_{\pi}(s,a)$ の値を更新するのが目的です.そこでNNの入力も,これと揃えて盤面の状態そのもの+選択したアクションとします.
計算結果を$r+q_{\pi}(s', \pi(s'))$に近づけたいため,これを「正解の値」として,NNの学習処理を行います.あくまで「関数近似」の領域ですが,データ収集&学習処理を繰り返すことで,どんどん性能(近似精度)が良くなると期待できます.
以上が今回用いたDQNの全貌です.具体的な話はコードを見た方が早いと思うので,後に回します.
2-4. 世界観まとめ
理論編が予想以上に長くなってしまいました(ガチ).全体像をここでまとめ直して実装パートに移ります.
- 強化学習では,エージェントにゲームをプレイさせ,得られる報酬を最大化するように行動ポリシーを改善していく.
- 行動-状態価値関数の値をあらゆる状態・アクションについて正確に求められれば,すべての盤面での最善手がわかったことになる.
- オフポリシーでデータ収集を行い,随時 行動-状態価値関数の値の更新を行っていくのがQ-Learningである.
- 状態数が多すぎる場合はそのままだと手に負えないので,ニューラルネットワークを用いて行動-状態価値関数を近似して計算,さらにデータを集めてこのNNの学習処理を行う.(DQN)
以上ですお疲れさまでした!よくわからんという場合も,コードを読んでみたらわかるかもしれないので行ったり来たりしてみてください.単純に私の理論まとめが良くないだけだったら申し訳ありません.少なくとも足りない部分はあるはずなので,もっときちんとお勉強されたい方は,何か他の書籍等に当たってみるといいかと思います.
今度こそ本当に理論終わりですコードに移ります↓↓
3. 実装
それではコードをどんどん載せていきます.おそらく上からベタ貼りして頂ければ,再現することも可能かと思います(乱数が絡むコードだらけなので,完全に同じ結果が得られるはずはないですが).また各所にお見苦しいコードが見られるかと思いますがお許しください.
とりあえずimportすべきものだけここに貼っておきます.以下のコードはすべてこの前提でお願いします.(実は不要なモジュールが含まれてるかもですがご了承ください)
import numpy as np
import copy, random, time
from tensorflow.keras import layers, models
from IPython.display import clear_output
import matplotlib.pyplot as plt
import seaborn as sns
import matplotlib
matplotlib.rcParams['font.size'] = 20
import pickle
from tensorflow.keras.models import load_model
3-1. Gameクラスの定義
まずはコード上で2048ゲームを実装します.やったらと長いですが中身は薄いですのでそのつもりで眺めてください.このコードに限らずですが,後ろに日本語解説をつけていますのでそちらを見てからの方がよいかもしれません.では.
class Game:
def __init__(self):
self.restart()
def restart(self):
self.board = np.zeros([4,4])
self.score = 0
y = np.random.randint(0,4)
x = np.random.randint(0,4)
self.board[y][x] = 2
while(True):
y = np.random.randint(0,4)
x = np.random.randint(0,4)
if self.board[y][x]==0:
self.board[y][x] = 2
break
def move(self, a):
reward = 0
if a==0:
for y in range(4):
z_cnt = 0
prev = -1
for x in range(4):
if self.board[y][x]==0: z_cnt += 1
elif self.board[y][x]!=prev:
tmp = self.board[y][x]
self.board[y][x] = 0
self.board[y][x-z_cnt] = tmp
prev = tmp
else:
z_cnt += 1
self.board[y][x-z_cnt] *=2
reward += self.board[y][x-z_cnt]
self.score += self.board[y][x-z_cnt]
self.board[y][x] = 0
prev = -1
elif a==1:
for x in range(4):
z_cnt = 0
prev = -1
for y in range(4):
if self.board[y][x]==0: z_cnt += 1
elif self.board[y][x]!=prev:
tmp = self.board[y][x]
self.board[y][x] = 0
self.board[y-z_cnt][x] = tmp
prev = tmp
else:
z_cnt += 1
self.board[y-z_cnt][x] *= 2
reward += self.board[y-z_cnt][x]
self.score += self.board[y-z_cnt][x]
self.board[y][x] = 0
prev = -1
elif a==2:
for y in range(4):
z_cnt = 0
prev = -1
for x in range(4):
if self.board[y][3-x]==0: z_cnt += 1
elif self.board[y][3-x]!=prev:
tmp = self.board[y][3-x]
self.board[y][3-x] = 0
self.board[y][3-x+z_cnt] = tmp
prev = tmp
else:
z_cnt += 1
self.board[y][3-x+z_cnt] *= 2
reward += self.board[y][3-x+z_cnt]
self.score += self.board[y][3-x+z_cnt]
self.board[y][3-x] = 0
prev = -1
elif a==3:
for x in range(4):
z_cnt = 0
prev = -1
for y in range(4):
if self.board[3-y][x]==0: z_cnt += 1
elif self.board[3-y][x]!=prev:
tmp = self.board[3-y][x]
self.board[3-y][x] = 0
self.board[3-y+z_cnt][x] = tmp
prev = tmp
else:
z_cnt += 1
self.board[3-y+z_cnt][x] *= 2
reward += self.board[3-y+z_cnt][x]
self.score += self.board[3-y+z_cnt][x]
self.board[3-y][x] = 0
prev = -1
while(True):
y = np.random.randint(0,4)
x = np.random.randint(0,4)
if self.board[y][x]==0:
if np.random.random() < 0.2: self.board[y][x] = 4
else: self.board[y][x] = 2
break
return reward
Gameクラスには,boardとscoreを管理させることにしました.名前の通り盤面と現時点でのスコアです.boardは2次元のnumpy配列で表現しています.
restartメソッドによって,盤上ランダムな2箇所に「2」のタイルを置き,スコアを0にしてゲームをスタートします.(1章のルール説明において,初期盤面では「2」か「4」が置かれていると言いましたが,コード上は「2」しか湧かなくなっています.これは筆者がGameクラス実装時,はじめは「2」だけだと勘違いしていたせいです.ゲーム性にはほぼ影響ないので許してください.)
moveメソッドは,アクションの種類を引数としてとり,それに応じてboardを変化,スコアを加算します.返り値としてこの1ターンで加算された分のスコアを返していますが,これはのちに利用します.(今回の学習において,エージェントが獲得する「報酬」としてはゲーム内のスコアをそのまま採用しました).アクションは0~3の整数で表現し,それぞれ 左,上,右,下,と対応づけました.board変化の実装は無駄に長いインデックスこねこねで,おそらく可読性が低いです.真面目に読まなくても全然OKです.もっと綺麗に書けるのかもですがここは許してください(´×ω×`)
また最後のwhileループでは,1枚新たなタイルを生成しています.ここもアルゴリズム的には効率の悪い実装かもですが無理やり殴りました.反省してます.「2」または「4」のタイルが生成されるわけですが,筆者による軽い統計の結果「80%の確率で2が湧く」くらいだったのでそのように実装しました.実際には少しずれているかもですが今回はこれでいきます.
なおmoveメソッドは,「選択可能な」アクションが入力されることを前提にしています.(盤面が動かない方向はプレイ中選べないので.)これについては次の関数で.
3-2. 選択可能なアクションの判定
上のmoveメソッドへの入力時など,各盤面で,各アクションが「選択可能か」というのが知りたい場面が今後たくさん出てきます.そこで判定用関数としてis_invalid_actionを用意しました.盤面とアクションを与え,それが選べないアクションだった場合にTrueを返すので注意してください.
またこのコードはmoveメソッドと非常に似ており無駄に長いだけなので,下の三角マークに折りたたんであります.中身コピペしたらすぐ閉じちゃってください.ダサいので.
`is_invalid_action`
def is_invalid_action(state, a):
spare = copy.deepcopy(state)
if a==0:
for y in range(4):
z_cnt = 0
prev = -1
for x in range(4):
if spare[y][x]==0: z_cnt += 1
elif spare[y][x]!=prev:
tmp = spare[y][x]
spare[y][x] = 0
spare[y][x-z_cnt] = tmp
prev = tmp
else:
z_cnt += 1
spare[y][x-z_cnt] *= 2
spare[y][x] = 0
prev = -1
elif a==1:
for x in range(4):
z_cnt = 0
prev = -1
for y in range(4):
if spare[y][x]==0: z_cnt += 1
elif spare[y][x]!=prev:
tmp = spare[y][x]
spare[y][x] = 0
spare[y-z_cnt][x] = tmp
prev = tmp
else:
z_cnt += 1
spare[y-z_cnt][x] *= 2
spare[y][x] = 0
prev = -1
elif a==2:
for y in range(4):
z_cnt = 0
prev = -1
for x in range(4):
if spare[y][3-x]==0: z_cnt += 1
elif spare[y][3-x]!=prev:
tmp = spare[y][3-x]
spare[y][3-x] = 0
spare[y][3-x+z_cnt] = tmp
prev = tmp
else:
z_cnt += 1
spare[y][3-x+z_cnt] *= 2
spare[y][3-x] = 0
prev = -1
elif a==3:
for x in range(4):
z_cnt = 0
prev = -1
for y in range(4):
if spare[3-y][x]==0: z_cnt += 1
elif spare[3-y][x]!=prev:
tmp = state[3-y][x]
spare[3-y][x] = 0
spare[3-y+z_cnt][x] = tmp
prev = tmp
else:
z_cnt += 1
spare[3-y+z_cnt][x] *= 2
spare[3-y][x] = 0
prev = -1
if state==spare: return True
else: return False
3-3. 盤面の可視化
盤面見せる機能がなくてもAIくんは問題なく学習できますが,我々人間が寂しいので作りました.ただまあ本題はここではないので,という言い訳で相当手抜いてます.
def show_board(game):
fig = plt.figure(figsize=(4,4))
subplot = fig.add_subplot(1,1,1)
board = game.board
score = game.score
result = np.zeros([4,4])
for x in range(4):
for y in range(4):
result[y][x] = board[y][x]
sns.heatmap(result, square=True, cbar=False, annot=True, linewidth=2, xticklabels=False, yticklabels=False, vmax=512, vmin=0, fmt='.5g', cmap='prism_r', ax=subplot).set_title('2048 game!')
plt.show()
print('score: {0:.0f}'.format(score))
ヒートマップを用いて最低限の機能だけ再現しました(本当に最低限です).ここに関しては詳細を読む必要はなく,脳死コピペでいいと思います.実際どんなふうに見えるかは次で示します.
補足 ヒートマップにまつわる葛藤
本当にしょうもない話なのですが,2048ゲームを実装するにあたり,「数字を2の累乗ではなく単に1,2,3...と使う」という案がありました.理由としてはただ一点で,この可視化関数でそっちの方が綺麗に盤面が彩色されるからです.ただそれだとやはりゲームとして2048感が無いというのと,盤面の学習がうまく行えなさそう,という直感が働いたのとで結局こうなりました.そのせいで結局,見ればわかりますが小さい数字たちは非常に近い色合いで見づらくなってしまっています.対数軸で色が変わるヒートマップとか,ないんですか...?3-4. プレイしてみる
学習させたいだけならこの工程は完全に不要ですが,せっかくなのでpython版2048ゲームをプレイしてみよう,ということでこんな関数を書いてみました.これも相当手抜いてますし,真面目に読む必要なしです.頑張ればいくらでも快適なUIにできるでしょうが,本題ではないので置いときます.
def human_play():
game = Game()
show_board(game)
while True:
a = int(input())
if(is_invalid_action(game.board.tolist(),a)):
print('cannot move!')
continue
r = game.move(a)
clear_output(wait=True)
show_board(game)
これで human_play() と実行してしまえばゲーム開始です.0〜3までの数字を入力して盤面を動かしてください.
こんな感じで盤面が現れて遊べます.やっぱり盤面見にくいですね.ちなみにこのコードだと,誤って数字以外の入力をしてしまった瞬間バグって問答無用でゲームオーバーです.UIなんて知りません.またこれはゲーム終了判定をつけていないので,動かせなくなったら先の仕様を逆手にとって,変な入力をしてゲームから抜け出しましょう.UIなんて知りません.
このタイミングで,コンピューターにもこのゲームをプレイさせてみましょう.
def random_play(random_scores):
game = Game()
show_board(game)
gameover = False
while(not gameover):
a_map = [0,1,2,3]
is_invalid = True
while(is_invalid):
a = np.random.choice(a_map)
if(is_invalid_action(game.board.tolist(),a)):
a_map.remove(a)
if(len(a_map)==0):
gameover = True
is_invalid = False
else:
r = game.move(a)
is_invalid = False
time.sleep(1)
clear_output(wait=True)
show_board(game)
random_scores.append(game.score)
コンピューターにプレイさせると言いましたが,完全ランダムで手を選んだ場合の様子を眺めることができる,という関数です.引数として適当な配列をとります(伏線).眺める分にはこの引数はどうでもいいので, random_play([]) のように適当に実行してみましょう.アニメーションのようにゲームが進みます.
眺めているとわかりますが,この段階では意志を持ってプレイしている感が全くありません(ランダムなので当然).そこでこの時点での実力(平均スコアなど)を把握しておきましょう.引数として配列をとっていたのはこれを行うためです.random_play 関数において,盤面の可視化に関わるコード(上から3行目と,下から2~4行目です)をコメントアウトしたのち,以下のコードを実行してみましょう.
random_scores = []
for i in range(1000):
random_play(random_scores)
print(np.array(random_scores).mean())
print(np.array(random_scores).max())
print(np.array(random_scores).min())
1000回テストプレイを行い,その平均点,最高点,最低点を調べてみました.意外とすぐに実行は終わります.実行ごとに結果は多少変わりますが,筆者の手元では
- 平均点:1004.676点
- 最高点:2832点
- 最低点:80点
という結果が出ました.これが何も学習していないAIの実力と言ってもいいでしょう.ということは,平均で1000点を優に上回るようになれば,多少なりとも学習はできていると言ってよいでしょう.また,1000回プレイの最高点がこの程度なので,スコア3000点越えというのは,運だけで到達することは難しい領域だと考えてよいかと思います.この辺りを基準にして,のちの学習結果を考察していきましょう.
3-5. ニューラルネットワークの作成
ここでは,行動-状態価値関数の値を計算する,さらには収集したデータを受けて学習を行う張本人である,ニューラルネットワークを実装します.とはいっても,この面倒なところはすべてTensorFlowに丸投げという形をとるので,ブラックボックスはブラックボックスと捉えていただいても結構です.とりあえずコードをベタ張りします.
class QValue:
def __init__(self):
self.model = self.build_model()
def build_model(self):
cnn_input = layers.Input(shape=(4,4,1))
cnn = layers.Conv2D(8, (3,3), padding='same', use_bias=True, activation='relu')(cnn_input)
cnn_flatten = layers.Flatten()(cnn)
action_input = layers.Input(shape=(4,))
combined = layers.concatenate([cnn_flatten, action_input])
hidden1 = layers.Dense(2048, activation='relu')(combined)
hidden2 = layers.Dense(1024, activation='relu')(hidden1)
q_value = layers.Dense(1)(hidden2)
model = models.Model(inputs=[cnn_input, action_input], outputs=q_value)
model.compile(loss='mse')
return model
def get_action(self, state):
states = []
actions = []
for a in range(4):
states.append(np.array(state))
action_onehot = np.zeros(4)
action_onehot[a] = 1
actions.append(action_onehot)
q_values = self.model.predict([np.array(states), np.array(actions)])
times = 0
first_a= np.argmax(q_values)
while(True):
optimal_action = np.argmax(q_values)
if(is_invalid_action(state, optimal_action)):
q_values[optimal_action][0] = -10**10
times += 1
else: break
if times==4:
return first_a, 0, True #gameover
return optimal_action, q_values[optimal_action][0], False #not gameover
QValueクラスという形で実装しています.このインスタンスが学習対象そのもの(正確にはそのメンバ変数 model ですが)になります.そして前半の build_model メソッドが,インスタンス生成時に実行され,ニューラルネットワークを作成する関数です.
build_model メソッドの概要を述べますが,それぞれの「NN語」についての詳しい解説はしません.ほーん,ぐらいでいいかと思います.知識のある方はべたべた読む価値はあると思います.(同時に改善の余地がボロボロ見えるかもしれません.ご教授ください...)
理論編でちょろっと話した,畳み込みニューラルネットワーク(CNN)を用います.盤面の2次元的な広がりを捉えることを期待したためです.入力としては,盤面にあたる4x4の配列と,アクションの選択にあたる長さ4の配列をとります.アクション選択は0~3の入力ではなく,4箇所のうち1つが1,残りが0の配列で表現するというOne-hotエンコーディングで行います.畳み込みには8種類の3x3フィルターを用います.パディングやバイアス,活性化関数についても指定します.
隠れ層として,ニューロン数が2048のもの,1024のものを1層ずつ用意し,最後に出力層を定義しました.隠れ層の活性化関数はReLUを用います.また,パラメータのチューニングに用いる誤差関数として,最小二乗誤差を採用しています.
NNについての説明はここで切り上げます.全くわからなかったという方も,中身は知らんけど要はNNを定義した,とだけ思ってくれればOKです.
もうひとつ,get_action というメソッドがあります.これは「ニューラルネットワークで行動-状態価値関数の値を計算する」というステップにあたります.盤面の状態 state を引数にとり,4種類のアクションのOne-hot表現を用意して,NNに4つの入力をぶち込みます.このぶち込みは,tensorflowにもともと用意されている predict メソッドで行えます.NNの出力としては,stateにおける4種類のアクションに対する行動-状態価値関数の値が返ってきます.このうち値が最大となるアクションを np.argmax 関数で取得する,というのがこのメソッドの大体の役割です.
後半ごちゃごちゃやってますが,これは行動-状態価値関数の値から選択されたアクションが,その盤面で選択可能か(動かすことができるか)を調べています.もし無理なら,次に行動-状態価値関数の値を大きくするアクションを選び直します.このついでに,このメソッドはゲームオーバーの判定も行っています.get_action メソッドの返り値は3つありますが,順に「選択されたアクション,その盤面・アクションに対する行動-状態価値関数の値,盤面がゲームオーバーか否か」としています.
3-6. 学習に基づきゲームをプレイする
先ほどは完全ランダムにプレイさせてみましたが,今回は学習結果を組み込んでプレイさせます.以下の get_episode 関数で,1ゲーム分のプレイが行われます.(強化学習では,1回のゲームのことをエピソードとよく呼びます.)
def get_episode(game, q_value, epsilon):
episode = []
game.restart()
while(True):
state = game.board.tolist()
if np.random.random() < epsilon:
a = np.random.randint(4)
gameover = False
if(is_invalid_action(state, a)):
continue
else:
a, _, gameover = q_value.get_action(state)
if gameover:
state_new = None
r = 0
else:
r = game.move(a)
state_new = game.board.tolist()
episode.append((state, a, r, state_new))
if gameover: break
return episode
episode という配列を用意して1ゲームプレイし,「現状態,選択したアクション,その際に得られた報酬,遷移した先の状態」を1セットにして,配列にどんどん格納していく,というのが基本動作です.ここで収集したデータを用いて,のちに学習処理を行います.アクションの選択には,先ほど定義した q_value.get_action メソッドを使います.これにより,その場で(かつ現状の実力で)最善と思われる手が選ばれます.また,このメソッドで行っていたゲームオーバー判定を生かし,エピソードの終了を感知しています.
1点注意すべきなのは,「毎ターン学習結果に従うとは限らない」ということです.get_episode 関数は引数に epsilon なるものをとっていますが,これは「プレイ中,学習結果に従わずにランダムでアクションを選択する確率」です.ランダムなアクション選択を混ぜることで,より多様な盤面を学習でき,より賢いAIになれると期待できます.
このように,「基本はGreedyポリシーでアクションを選択するが,確率 $\epsilon$ でランダムな行動を混ぜる」という行動ポリシーを,ε-Greedyポリシーと呼びます.εの値をどの程度に設定するかは,重要かつ難しい問題です.(通常0.1〜0.2程度とするらしいです.)
またこの関数は,epsilon=0 と設定することで,Greedyポリシーでプレイさせることができます.つまりはランダムなアクションを含まない,その時点での「AIの全力」のプレイです.AIくんの実力を測るための関数 show_sample を以下に示します.
def show_sample(game, q_value):
epi = get_episode(game, q_value, epsilon=0)
n = len(epi)
game = Game()
game.board = epi[0][0]
# show_board(game)
for i in range(1,n):
game.board = epi[i][0]
game.score += epi[i-1][2]
# time.sleep(0.2)
# clear_output(wait=True)
# show_board(game)
return game.score
といっても,基本は get_episode 関数を epsilon=0 のもと実行するだけで,それ以降はエピソードの記録を用いての盤面の再現です.将棋でいう棋譜を辿るようなものですね.関数内にコメントアウトされた部分がありますが,これを解除すると,アニメーションで眺めることができます.(random_play関数でもそうですが,time.sleep に与える数値を調整することで,アニメーションの速さを制御できます.)
また返り値として最終的なスコアを出力しています.これを用いて,学習処理のはざまに show_sample を挟むことで学習の成果をおおむね把握することができます.
それではいよいよ学習のアルゴリズムを実装しましょう!
3-7. 学習処理
NNに学習をさせる関数 train を定義します.少し長めですが,そんなに難しいことはしていないので落ち着いて読んでみてください.少し丁寧めに解説もいたします.
def train(game, q_value, num, experience, scores):
for c in range(num):
print()
print('Iteration {}'.format(c+1))
print('Collecting data', end='')
for n in range(20):
print('.', end='')
if n%10==0: epsilon = 0
else: epsilon = 0.1
episode = get_episode(game, q_value, epsilon)
experience += episode
if len(experience) > 50000:
experience = experience[-50000:]
if len(experience) < 5000:
continue
print()
print('Training the model...')
examples = experience[-1000:] + random.sample(experience[:-1000], 2000)
np.random.shuffle(examples)
states, actions, labels = [], [], []
for state, a, r, state_new in examples:
states.append(np.array(state))
action_onehot = np.zeros(4)
action_onehot[a] = 1
actions.append(action_onehot)
if not state_new:
q_new = 0
else:
_1, q_new, _2 = q_value.get_action(state_new)
labels.append(np.array(r+q_new))
q_value.model.fit([np.array(states), np.array(actions)], np.array(labels), batch_size=250, epochs=100, verbose=0)
score = show_sample(game, q_value)
scores.append(score)
print('score: {:.0f}'.format(score))
引数が5つあり,順に「Gameクラスのインスタンス game,学習対象のモデル(QValueインスタンス) q_value,学習を行う回数 num,収集したデータを入れておく配列 experience,学習成果(スコア)を入れていく配列 scores」です.詳細は追い追い.
num の分だけループを回しています.ここで「1回の学習」というのは,1ゲームプレイとは全く違います.1回の学習の流れを説明します.
学習は,データの収集とNNの更新という2ステップに分かれています.データ収集パートでは,get_episode 関数を20回起動しています(要は20回ゲームをプレイする).基本はε=0.1のε-Greedyポリシーでデータを収集しますが,20回中2回だけ,ランダムな行動を混ぜないGreedyポリシー(ε=0)でプレイし,データを集めます.このように2種類のプレイを混ぜることで,幅広い盤面を学び,かつ長めにゲームが進んだときの盤面も学習に組み込みやすくなるそうです.
収集したデータはすべて experience に入れられます.この配列の長さが50000を超えた場合,古いデータから削除していきます.またデータが5000個集まるまでは,次のモデル更新ステップはスキップしています.
モデル更新は,experience からデータを抽出し,新たに example 配列を作成して行います.その際直近のデータから1000個,残りの部分からランダムに2000個選び出し,シャッフルするという操作を施しています.こうすることで新しいデータを学習に組み込みつつ,かつ学習結果に偏りが出にくくなるようです.
次のfor文では,example の中身をひとつずつ見ていきます.NNの学習は,データひとつひとつを受けて行うよりも,まとめて入力した方が演算速度的な面で効率が良いので,その準備をしていきます.states,actions,labels にそれぞれ現状態の盤面,選択するアクションのOne-hot表現,そのときの行動-状態価値関数の「正解」の値,を入れていきます.
正解の値についてですが,これは理論編 2-2-3. TD法 あたりで説明したように,$r+q_{\pi}(s',\pi(s'))$ と設定することで,NNの出力がここに近づくように修正されます.これはコード上では r+q_new に相当します.q_newというのは「遷移先の状態からずっと現状のポリシーに従って行動した場合に得られる報酬の期待値」であり,これは q_value.get_action メソッドに次状態を与えたときの2つめの出力(次状態とそこでの最善手に対する行動-状態価値関数の値)に相当しますので,そのように取得します.なお,ゲームオーバー状態に対しては,q_new は0と定めています.
次の q_value.model.fit メソッドで,NNが学習を行います.この中身については別でオベンキョしてください.引数としてはNNの入力 states と actions,正解の値として labelsを与えています.batch_size や epochs は気にしなくてもよいですが,これらの値の設定は学習の精度に影響します(これが適切な設定である自信は全くないです).verbose=0 は,不要なログ出力を抑えているだけです.
fit メソッドによる学習処理が終わったら,show_sample 関数を起動して,AIくんに全力でプレイしてもらいます.その最終スコアをログとして出力しつつ,scores 配列に格納して,あとで平均点などを計算するのに使おう,という実装にしています.以上が「1回の学習」の全貌です.これを繰り返すのが train 関数です.
補足 `batch_size` と `epochs` について
これらは気にしなくていいと述べましたが,概要だけでも知っておく価値はあると思うので軽く整理します. NNの学習では,入力データを一気に学習するのではなく,**ミニバッチ**という小さなかたまりに分割してから,各バッチについて学習を行います.このバッチの大きさが `batch_size` です.上のコードでは入力のサイズが3000,batch_sizeが250なので,12個のミニバッチに分割されます. そして,入力データすべてについて1度学習処理を施すことを,**エポック**という単位で数えます.上のコードでは入力3000個,バッチにして12個分の学習で1エポックとなります.パラメータ `epochs` は,学習処理を何エポック繰り返すかを意味しています.ここではepochs=100としたので,バッチ分割→すべてについて学習 の流れを100回繰り返すことになります. 雑なまとめになりますが,ニューラルネットワークって難しいですね\(^^)/4. 学習実行&観察
以上でモデル・関数の実装はほぼ終了です.あとは実際に学習させて,成長の様子を眺めてみましょう!記事も気楽に書きます...
注意 ここで示す学習結果について
あたかも自分が実行したコードおよびその結果をそのまま記事に載せているかのような口ぶりですが,実際は色々いじりながら・修正しながら学習を進めたため,学習過程が一部異なります.(具体的には,はじめの30回ほどはε=0.2でデータ収集をしていたり,昔は `get_action` メソッドの仕様が少し違っていたり,です.途中でデータが吹っ飛んだりもしてます).その点だけご了承ください. また,この直後に示す10回分の学習の出力は後からコードを実行し直して補ったもの(当時の出力が吹っ飛んでました)で,今後べたべた考察していくモデルの学習記録とは異なります.あんまりじーっと見ないでください><4-1. trainしてみる
まずは Game クラスと QValue クラスのインスタンス,およびその他を生成します.
game1 = Game()
q_value1 = QValue()
exp1 = []
scores1 = []
1というナンバリングには特に意味はありません.なんとなくです.これだけで,もう学習の準備は完了です.train 関数を起動させてみましょう.
%%time
train(game1, q_value1, 10, exp1, scores1)
これだけです.これで10回分の学習が行われます.1行目の %%time はマジックコマンド的なもので,実行にかかった時間を計測してくれます.何故そんなことをするかというと,学習には非常に時間がかかるからです.この10回だけで平気で30分くらいかかります.ただ train 関数は,進捗状況を随時出力するような実装にしているため,先の見えない暗闇を進むよりは気が楽です.のんびり待ちながら,出力を眺めてみましょう.
Iteration 1
Collecting data....................
Iteration 2
Collecting data....................
Iteration 3
Collecting data....................
Training the model...
score: 716
Iteration 4
Collecting data....................
Training the model...
score: 908
Iteration 5
Collecting data....................
Training the model...
score: 596
...
Iteration 3のように,現在何回目のループかがすぐにわかります.Collecting data... と表示されている間はデータ収集パート,Training the model... の間はモデル更新パートです.はじめの2回は exp1 の長さが5000に達しておらず,モデル更新がスキップされています.
1回の学習が終わるごとに,ランダムなアクションなしで1ゲームプレイし,そのスコアが表示されています.この結果は scores1 に格納されていくので,あとから統計をとるなりできます.
あとはこれをひたすら繰り返すだけです.追加で90回学習を行うには以下のコードを実行しましょう.
%%time
train(game1, q_value1, 90, exp1, scores1)
exp1 や scores1 は再利用され,完全に前回の続きから学習が進められます.
やってみればわかりますが,この学習には本当に時間がかかります.筆者の環境では,100回につき5~6時間が目安といった感じでしょうか.ここ最近は筆者が寝ている間にも,Macくんは夜通し唸ってました.もし興味のある方は,地道に時間を見つけて演算を進めていくと同じ体験ができるかと思います.
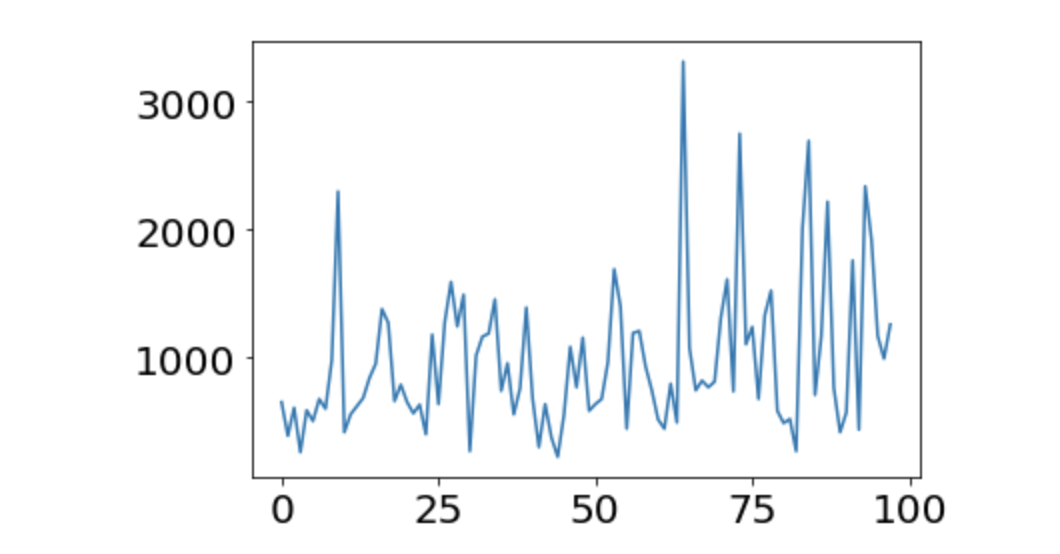
100回の学習が終わったとして,その最中での「全力スコア」の変化を雑にプロットしてみます.scores1 を使います.
x = np.arange(len(scores1))
plt.plot(x, scores1)
plt.show()
んー.これはちょっと学習ができているとは言い難いですね.平均点は974.45点でした.全然伸びてない.もう少し学習が必要そうです.
4-2. 学習結果を一時保存する
この学習は長旅になりそうなので,保存方法だけ確立させておきましょう.pythonのpickleという機能で,exp1 や scores1 を保存できます.tensorflowのモデルにはpickleが使えませんが,save機能がもともと用意されています.以下にコードを示すので,わかりやすい名前で保存してください.
wfile = open('filename1.pickle', 'wb')
pickle.dump(exp1, wfile)
pickle.dump(scores1, wfile)
wfile.close()
q_value1.model.save('q_backup.h5')
保存しておいたオブジェクトを取り出すには以下のようにします.
myfile = open('filename1.pickle', 'rb')
exp1_r = pickle.load(myfile)
scores1_r = pickle.load(myfile)
q_value1_r = QValue()
q_value1_r.model = load_model('q_backup.h5')
名前の後ろにつけたrはrestoreの頭文字のつもりです.q_value1 の方は,QValueインスタンスではなくその中のmodelを保存しているので,インスタンスだけ生成したのち,modelをロードして置き換えます.なお,Gameクラスのインスタンスは特に学習しているわけではないので,必要なときに新しく作成しても問題ありません.
こんな感じで学習の記録をこまめに残しておくことを勧めます.途中でデータが飛んだときの対策になるのはもちろん,学習途中のモデルをあとから引っ張ってきて性能を比較することも可能になります.(筆者はこれを怠ったので後悔しています.)
4-3. trainを繰り返す
100回学習したモデルはまだまだ未熟者,という感じでしたので,ひたすら train 関数を回しました.結論から言うと1500回分学習してもらいました.ノンストップでも丸4日くらいかかるので,マネしたい場合は覚悟してください...
とりあえず1500回分の scores を軽く分析してみました.scoresを学習100回ずつで,得点帯を1000点ずつで区切り,各得点帯のスコアが出たかを表にしました.平均点も算出したので並べます.言葉でダラダラ説明するのもアレなので,もうベタッと表を貼ります.(参考までに,いつぞやの完全ランダム1000回プレイの得点分布も載せます.)
| 学習回数 | 0000~ | 1000~ | 2000~ | 3000~ | 4000~ | 5000~ | average |
|---|---|---|---|---|---|---|---|
| ランダム | 529 | 415 | 56 | 0 | 0 | 0 | 1004.68 |
| 1~100 | 61 | 30 | 6 | 1 | 0 | 0 | 974.45 |
| 101~200 | 44 | 40 | 9 | 6 | 1 | 0 | 1330.84 |
| 201~300 | 33 | 52 | 12 | 1 | 0 | 0 | 1234.00 |
| 301~400 | 35 | 38 | 18 | 7 | 2 | 0 | 1538.40 |
| 401~500 | 27 | 52 | 18 | 3 | 0 | 0 | 1467.12 |
| 501~600 | 49 | 35 | 11 | 4 | 1 | 0 | 1247.36 |
| 601~700 | 23 | 50 | 20 | 5 | 2 | 0 | 1583.36 |
| 701~800 | 45 | 42 | 11 | 2 | 0 | 0 | 1200.36 |
| 801~900 | 38 | 42 | 16 | 4 | 0 | 0 | 1396.08 |
| 901~1000 | 19 | 35 | 40 | 4 | 0 | 2 | 1876.84 |
| 1001~1100 | 21 | 49 | 26 | 3 | 1 | 0 | 1626.48 |
| 1101~1200 | 22 | 47 | 18 | 13 | 0 | 0 | 1726.12 |
| 1201~1300 | 18 | 55 | 23 | 4 | 0 | 0 | 1548.48 |
| 1301~1400 | 25 | 51 | 21 | 2 | 1 | 0 | 1539.04 |
| 1401~1500 | 33 | 59 | 7 | 1 | 0 | 0 | 1249.40 |
ふむ.どうでしょうか.学習が進むにつれてじわじわと平均点が伸びています.ランダム1000回プレイでは1回も到達できなかった3000点というひとつのラインも,少し学習を進めたあとはそこそこ出るようになっています.とりあえず,「学習の爪痕は残せている」と言うことはできるでしょう.
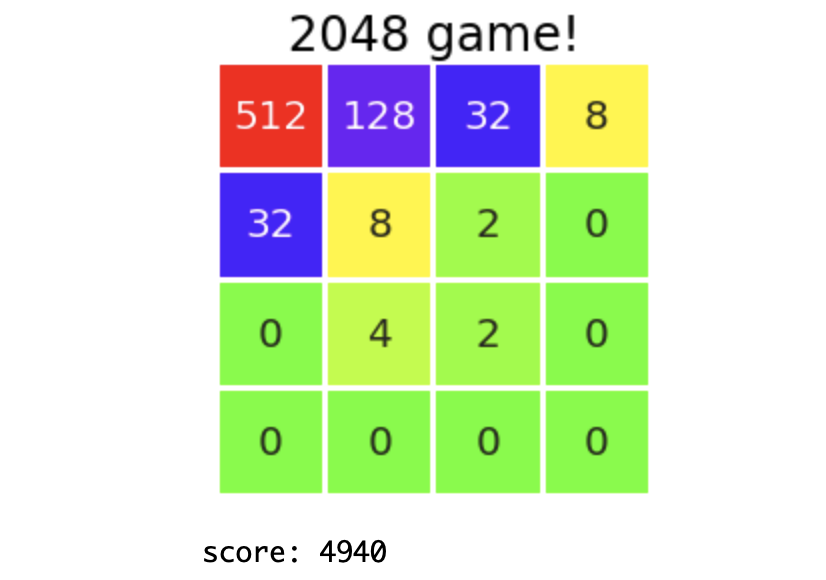
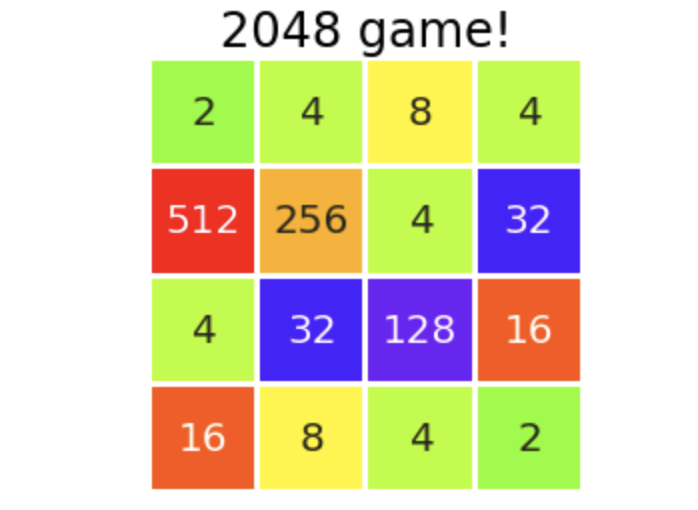
また,学習後のAIくんのプレイを眺めていると,以前とは違い何らかの意志を感じました(まあ人間が勝手に規則性を見出しているだけですが).瞬間盤面だけだとわかりにくいかもですが,そのシーンを切り取ってきたのでご紹介します.
荒削りな部分は多いですが,右下隅に大きい数を集める,という方針が見られました.これは,1-2. このゲームのコツ で私が紹介した方法と同じです.別にこちらから「角にでかい数字を集めるように学べ」的な実装をしたわけではないのに,このコツが学習できてきているのは興味深いですね.個人的にはかなり感動しました.
ただそれでも,4000点以上はなかなか出せていないというのが現実です.1500回で学習を止めたのは,単に時間の問題と,ご覧の通りスコアの伸びが止まったように感じたからです.実際のところはわかりませんが,このまま同じ学習アルゴリズムを適用し続けても,明確に性能が上がることはあまり期待できないと感じました.
後半スコアが伸びなかったどころか落ち込み気味なのは,たまたま運が悪かったことも考えられますが,なんとなく普通に性能が落ちているような気がしました.もう少しきちんと述べると,学習に使うデータ experience の中身の質が落ちた(先へ進んだ盤面があまり学習できない悪循環に陥った)のではないかと勝手に推測しています.とにかく,1500回学習後のモデルが現状最強だとは言えないと考えます.
上の表をじーっと見て,暫定の最強AIとして「1200回学習を終えた時点でのモデル」を選びました.まあ割と五十歩百歩ではあるんですが.冷凍保存しといてよかった.なぜ最強を選んだのかというと,次で「学習済みモデルはそのままに,より良い手を選びそうなアルゴリズム」を実装するからです.
というわけでこのときのモデルくんをロードしておきます.この子にはもう少し頑張ってもらいましょう.
game1200 = Game()
q_value1200 = QValue()
q_value1200.model = load_model('forth_q_value1_1200.h5')
※私がこの名前でモデルを保存してただけなので,このコードをベタ貼りされても普通に無理です.この先は,現状ご自分の環境で学習を進めてモデルを作成して頂かないと再現は無理なのが現状です.ごめんなさい.学習済みモデルをどこかで共有するの面倒なんだけど需要あるかな...
4-4. 1手先を読む
この先は学習を行うわけではありません.NNのモデルはそのままに,より上手くゲームをプレイできそうな行動ポリシーを作ります.(コードもう終わりとか言ってごめんなさい.まだあります.)
今までは与えられた状態に対し,「全アクションについて行動-状態価値関数の値を計算し,それが最大となるアクションを選ぶ」という行動ポリシーでした.get_action メソッドで行われていた処理がこれにあたります.これを改良して,「次状態のさらに1手先を読み,最善と思われる手を選ぶ」というアルゴリズムを実装します.まずはコードを貼ります.
def get_action_with_search(game, q_value):
update_q_values = []
for a in range(4):
board_backup = copy.deepcopy(game.board)
score_backup = game.score
state = game.board.tolist()
if(is_invalid_action(state, a)):
update_q_values.append(-10**10)
else:
r = game.move(a)
state_new = game.board.tolist()
_1, q_new, _2 = q_value.get_action(state_new)
update_q_values.append(r+q_new)
game.board = board_backup
game.score = score_backup
optimal_action = np.argmax(update_q_values)
if update_q_values[optimal_action]==-10**10: gameover = True
else: gameover = False
return optimal_action, gameover
従来の get_action メソッドに代わる関数,get_action_with_search です.4つのアクションについてforループを回します.現状態から,まず1回アクションaを選択して次状態へ遷移します.この際の報酬rを保持しておき,次状態からさらに次の一手を考えます.これが q_value.get_action(state_new) にあたります.このメソッドは2つ目の出力として最善のアクションに対する行動-状態価値関数の値を返すので,それを q_new として受け取ります.ここで r+q_new は,「現状態からアクションaを選択して得られる報酬と,その遷移先からの行動-状態価値関数の値の最大値の和」となります.4種類のアクションaについてこの値を求め,これが最大化するようなアクションを選ぶ,というのがこの関数の仕組みです.(ゲームオーバー判定も同時に行っています.)
このポリシーは比喩とかではなく1手先を読んでいるため,従来のアクション選択に比べ,最善手を選ぶ精度がより上がっていると期待できます.他の関数にも,get_action_with_search を組み込みましょう.
`get_episode2`
def get_episode2(game, q_value, epsilon):
episode = []
game.restart()
while(True):
state = game.board.tolist()
if np.random.random() < epsilon:
a = np.random.randint(4)
gameover = False
if(is_invalid_action(state, a)):
continue
else:
# a, _, gameover = q_value.get_action(state)
a, gameover = get_action_with_search(game, q_value)
if gameover:
state_new = None
r = 0
else:
r = game.move(a)
state_new = game.board.tolist()
episode.append((state, a, r, state_new))
if gameover: break
return episode
`show_sample2`
def show_sample2(game, q_value):
epi = get_episode2(game, q_value, epsilon=0)
n = len(epi)
game = Game()
game.board = epi[0][0]
# show_board(game)
for i in range(1,n):
game.board = epi[i][0]
game.score += epi[i-1][2]
# time.sleep(0.2)
# clear_output(wait=True)
# show_board(game)
show_board(game)
print("score: {}".format(game.score))
return game.score
↑とは言ったものの,本当にアクション選択の関数をすり替えただけで他は全く同じですので折りたたんでおきます.中身見て理解したらすぐ閉じちゃってください.
これで本当に足掻きは終わりです最後に成果を確認して終わります!
4-5. 最終結果
ちょっと前に暫定最強として認定した q_value1200 くんを持ってきます.この子に100回全力プレイしてもらい,4-3. trainを繰り返す で行ったような分析をしました(あとで載せます).
scores1200 = []
for i in range(100):
scores1200.append(show_sample(game1200, q_value1200))
さらに同じモデルを使い,1手先読みアルゴリズムを用いて同じく100回プレイしてもらいました.
scores1200_2 = []
for i in range(100):
scores1200_2.append(show_sample2(game1200, q_value1200))
結果を整理します.
| モデル | 0000~ | 1000~ | 2000~ | 3000~ | 4000~ | 5000~ | 6000~ | average |
|---|---|---|---|---|---|---|---|---|
| 通常 | 15 | 63 | 17 | 5 | 0 | 0 | 0 | 1620.24 |
| 1手先読み | 5 | 41 | 32 | 11 | 6 | 2 | 3 | 2388.40 |
はい.従来のアルゴリズムの方はまあ以前見たモデルたちと同等の性能ですが,1手先読みを導入した方はこれは明らかに性能が上がっています.嬉しい.特に6000点越えが3回と,流れがよければ高得点を狙えるポテンシャルがあるのがなんかいいですね.100回中最高点は6744点でした.そのときの最終盤面を載せます.
最後なので乱れちゃってはいますが,割と私たち人間がやってもわんちゃん負ける,そのレベルでのプレイができてそうです.遠い昔に設定した「自分より高スコアをとる」という目標には到底届いていませんが,ひとまずこのあたりで改良は打ち止めようと思います.夏休みももう終わりですし.(いやてか自分のハイスコア69544点って強すぎない...?)
5. おわりに
お疲れさまでした!(ここまで読んでくださった方がもしいればそれは本当にお疲れさまでした.ガチで).拙い上に長々と書き連ねてしまい申し訳ありませんでした.
振り返ってですが,やはりもう少し性能を上げたかったなというのが本音です.ハイスコアとしては悪くないですが,平均点的にはせいぜい人間の初見プレイ程度の知能しか得られていないので...
本当はここからの改善案についてももう少し考察しようと思っていたのですが,また長くなりすぎてしまいそうなのと,明日から急に授業が始まるピンチ(現在AM3:00)ということで,メモ書き程度にして未来の自分にパスしようかと思います.
- 単純にもう少し学習を重ねてみる.(ちょっと厳しい気がするけど...)
-
epsilonの値を変えてみる.(上げるか下げるかもわからん.ただ学習を進めるにつれεを小さく,とかは試してみる価値はあるかもしれない.) -
experienceの長さ,およびexampleの長さを大きく?してみる.(学習が進むほど1エピソードが長くなるし.現状のはあまり適切じゃないのかもしれない.) - CNNへの盤面の入力を,ひとつにまとめてではなくタイルごとに分けてみる.(これは結構見込みがあると思ってる.現状NNは「2」と「4」のタイルをあまり区別できてないんじゃないか?みたいな懸念.おそらく計算量は増えるけど,タイルごとに明確に意味が異なるのだから,分けて入力すべきな気もする.)
-
batch_sizeやepochsをいじる.(これは理解度不足だけど学習精度に影響するよね...という感じ.適切な値を探れる気がしない.) - 自分(筆者)がプレイしている様子を学習させてみる.(時間的な意味で相当めんどそうだけど成果は出そう.将棋とかもプロの棋譜を学習させてるって聞くし.うまく実装できるかな...)
- もっと先の手まで読んでプレイ.(まあいいんだけど,なんかなあ...感がやばい)
ざっとこんな感じでしょうか.せいぜい独学&勉強不足の私が思いつく程度の案ですので,もっとこうしてみたらいい,など教えて頂けるととても嬉しいです.(逆に私に代わってこれらの改善案を試してみるなども是非やってみてください.)
ここまで真面目にまとめてみると,1度理解したつもりの理論からホイホイ間違いやら新発見やらが出てきてとてもよかったです.またいつか弾丸で自由研究したら,こんな感じで記事にするかもしれないので新作をお待ちください.2048ゲームAIくんをもう少し追求するかもしれません.
それでは本当におしまいです.おもしろいな,と思った方は是非強化学習の世界にもっと深く踏み込んでみてください!
おしまい
夏休み終了に1日だけ間に合わなかった.許して.