pymc3でガウス過程

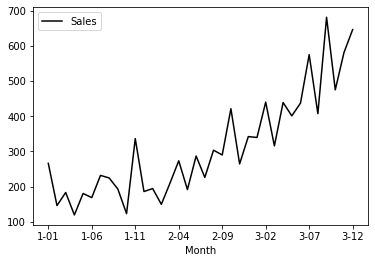
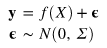こちらのサイトで見つけたシャンプーの売上に関するデータを用いてGaussian Processによって推定してみようと思います。

ガウス過程はノンパラメトリックの代表的な回帰モデルです。
非線形性のあるデータに強かったり、推定の不確実性を確認できるといったメリットがあります。

import os
import pandas as pd
shampoo_df = pd.read_csv('../data/shampoo.csv')
shampoo_df
shampoo_df.plot.line(x='Month', y='Sales',c="k");

以下では、適切な尤度と事前分布のペアを得るために、周辺尤度を算出しています。

with pm.Model() as shampoo_model:
    ρ=pm.HalfCauchy('ρ', 1) # これらはLength scale 大きい値ほど、近い動きに見える　<＝自己相関的な
    η = pm.HalfCauchy('η', 1) # これらはLength scale 大きい値ほど、近い動きに見える　<＝自己相関的な
    
    M = pm.gp.mean.Linear(coeffs=(shampoo_df.index/shampoo_df.Sales).mean()) # 初期値
    K= (η**2) * pm.gp.cov.ExpQuad(1, ρ)

    σ = pm.HalfCauchy('σ', 1)
    gp = pm.gp.Marginal(mean_func=M, cov_func=K) 
    gp.marginal_likelihood("recruits", X=shampoo_df.index.values.reshape(-1,1), 
                           y=shampoo_df.Sales.values, noise=σ)
    trace = pm.sample(1000)

pm.traceplot(trace);

最尤推定は、尤度関数p(X｜θ)をパラメータθに関して最大化することで当てはまりの良いモデルを作って行くのですが、事前分布p(θ)を使いません。一方、事前分布がある場合を最大事後確率推定というらしいです。

詳しくは以下の本を参照ください。
須山敦志. 機械学習スタートアップシリーズ　ベイズ推論による機械学習入門 (Japanese Edition) (Kindle Locations 2154-2156). Kindle Edition.

最大事後確率推定によって最適なパラメータを得る。

with shampoo_model:
    marginal_post = pm.find_MAP()

{'ρ_log__': array(2.88298779),
'η_log__': array(5.63830367),
'σ_log__': array(4.13876033),
'ρ': array(17.86757799),
'η': array(280.98567051),
'σ': array(62.72501496)}

X_pred=np.array([r for r in range(X_pred.max()+10)]).reshape(-1,1)

with shampoo_model:
    shampoo_pred = gp.conditional("shampoo_", X_pred)
    samples=pm.sample_ppc([marginal_post], vars=[shampoo_pred] ,samples=100)



fig = plt.figure(figsize=(10,5)); 
ax = fig.gca()

from pymc3.gp.util import plot_gp_dist
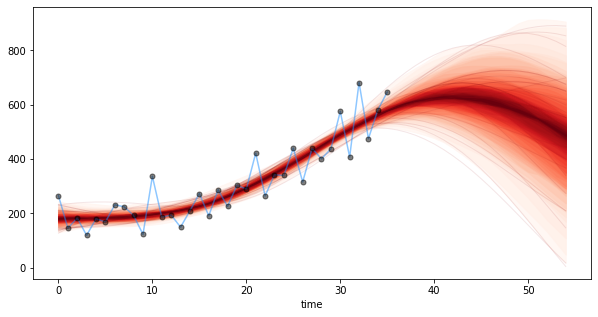
plot_gp_dist(ax, samples["shampoo_"], X_pred);

ax.plot(shampoo_df.index, shampoo_df.Sales, 'dodgerblue', ms=5, alpha=0.5);
ax.plot(shampoo_df.index, shampoo_df.Sales, 'ok', ms=5, alpha=0.5);
plt.show()

pm.sample_ppcではmarginal_post内のパラメータに基づく事後予測分布からサンプリングしています。