pymc3でアヒル本8章をやってみた

この記事は、「StanとRでベイズ統計モデリング」(アヒル本)という本をpymc3で実装したものです。

ベイズに関しては他にもたくさん記事があるので、ここでは割愛させていただきます。

この記事では、上記の本第8章の階層ベイズに関するトピックについてpymc3による実装をしてみます。

1. データ

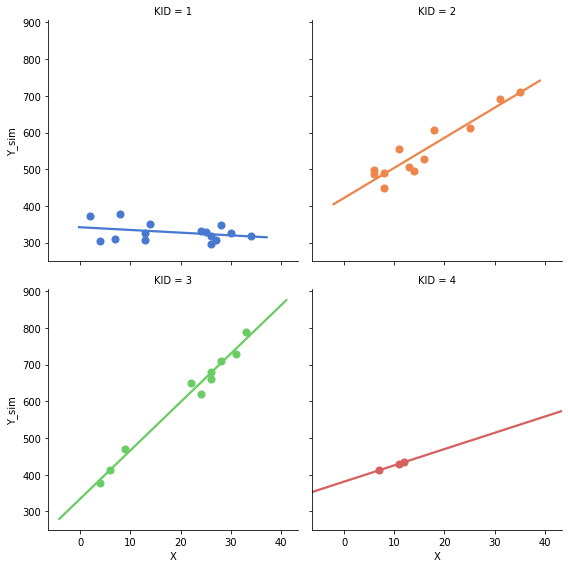
アヒル本の8.1.4で使っているデータは、大手４社の社員の年齢と年収などに関するデータをシミュレーションで作成したものです。
多少は異なりますが、同じようにデータを生成してみました。

変数の説明

Y_sim: 年収

X: 年齢(23を引いた値)

KID: 会社のID(0~3)

列間の相関を確認

・　YとXが正の相関、つまり年功賃金が考慮されたシミュレーションデータになっています。

2. モデル

3. 実装

df["KID"]=df["KID"]-1
n_KID=len(df["KID"].unique())
kids=df["KID"].values

with pm.Model() as hierarchical_model:
    mu_a = pm.Normal('mu_a', mu=0., sd=1000)
    sigma_a = pm.HalfNormal('sigma_a', 1000.)
    mu_b = pm.Normal('mu_b', mu=0., sd=10)
    sigma_b = pm.HalfNormal('sigma_b', 10.)

    a = pm.Normal('a', mu=mu_a, sd=sigma_a, shape=n_KID)
    b = pm.Normal('b', mu=mu_b, sd=sigma_b, shape=n_KID)
    eps = pm.HalfCauchy('eps', 5.)

    y_est = a[kids] + b[kids]*df.X.values

    y_like = pm.Normal('y_like', mu=y_est,
                           sd=eps, observed=df.Y_sim)
    trace=pm.sample(1000)

(初期値の設定は粗めです)

4. 結果

pm.traceplot(trace);

aとbはパラメータですがしっかりと会社ごとに区間が推定されていることがわかります。

"""
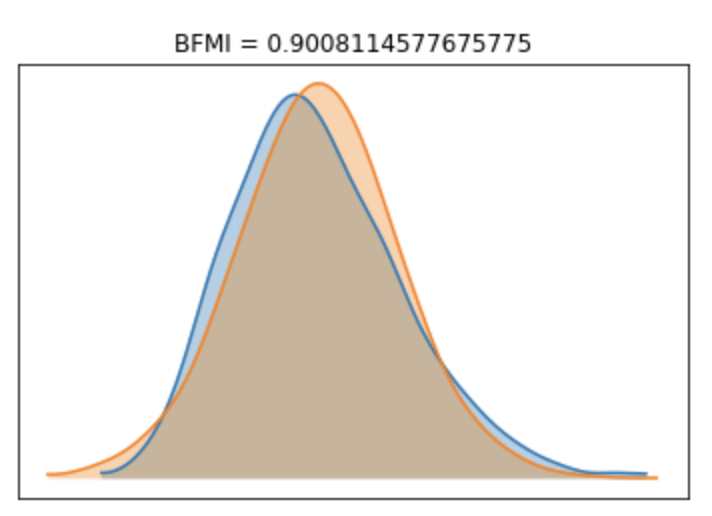
BFMIが0.3よりも大きいため程々に良いモデルと今回は解釈する
"""
bfmi = np.max(pm.stats.bfmi(trace))
(pm.energyplot(trace, legend=False, figsize=(6, 4))
   .set_title("BFMI = {}".format(bfmi)));

BFMIは0.3以上あると良いと言われているようです。