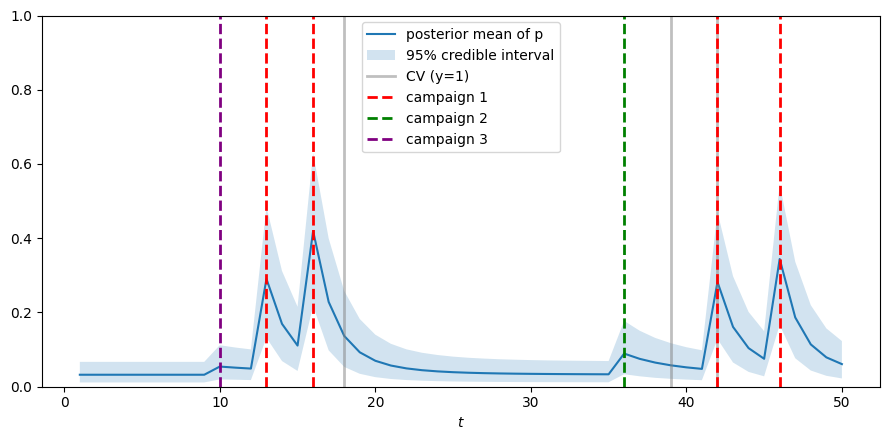
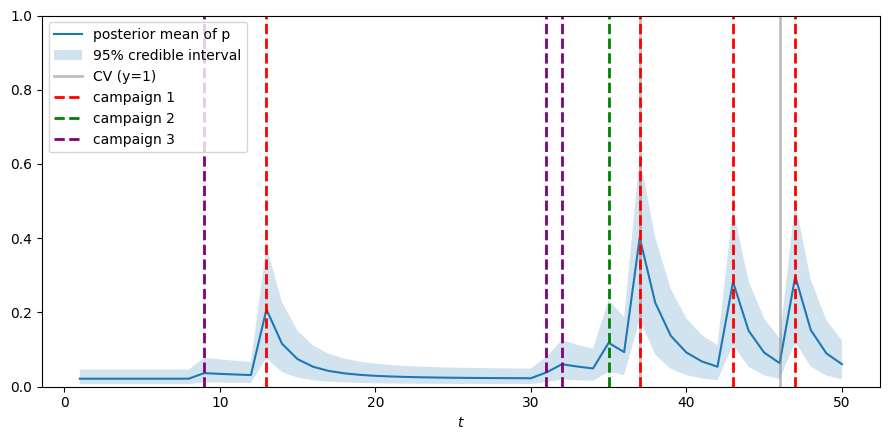
複数の施策が走っている状況において,個別施策の効果を分離した上で,時間経過に伴う施策効果の減衰と複数の施策効果の蓄積を推定したいケースがあると思います.
以下のように,あるユーザーに施策が当たるとそのユーザーの購買意欲が上がるが,時間とともに減衰し,また別の施策が当たると購買意欲が上がり...というイメージです.
このようなケースにおいて,施策交換減衰と蓄積を推定できるベイズ的なモデルを説明します.
モデル
まず,以下のように各施策効果が減衰していくと仮定します.
- 施策接触直後:$\tau$
- 1期後:$\lambda\tau$
- 2期後:$\lambda^2\tau$
- ・・・
$\tau=1$として$\lambda$を変更して施策効果の減衰を表現した図は以下です.
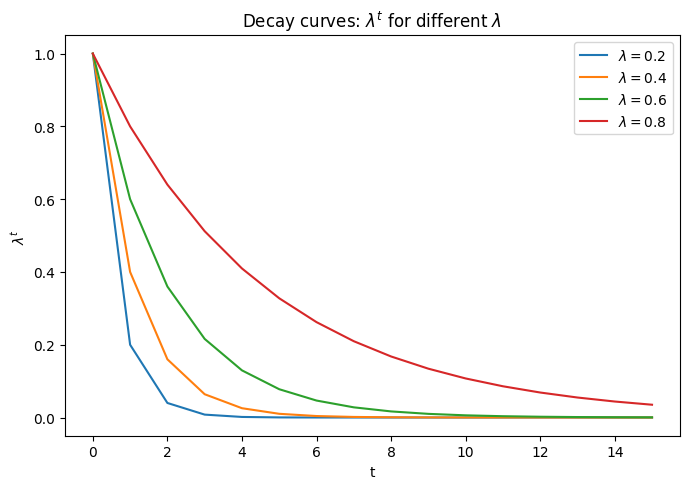
また,別の施策の効果は単純に加算されることを想定します.
そして,観測は二値を考えるため,ロジットモデルに従うと仮定します.
整理すると以下のようなモデルになります.
\begin{align*}
z_{it} &= \alpha_i + \sum_{s=1}^{t} \sum_{j=1}^J \lambda_j^{t-s} \tau_j x_{isj} \\
p_{it} &= \text{logit}^{-1}(z_{it}) \\
y_{it} &\sim \text{Bernoulli}(p_{it})
\end{align*}
ここで,$\text{Bernoulli}(p)$は確率$p$のベルヌーイ分布で,$\text{logit}^{-1}$は逆ロジット変換です.
また,各変数は以下です.
- $x_{isj}$:ユーザー$i$が$s$時点で施策$j$に接触したかどうか($0$または$1$)
- $y_{it}$:ユーザー$i$が$t$時点でCVしたかどうか($0$または$1$)
- $z_{it}$:ユーザー$i$の$t$時点でのCV率を決める潜在変数
- $p_{it}$:ユーザー$i$の$t$時点でのCV率
- $\alpha_i$:ユーザー$i$のベースライン
- $\lambda_j \in (0, 1)$:施策$j$の減衰スピードを決めるパラメータ
- $\tau_j$:施策$j$の接触直後の施策効果
- $J$:施策の種類数
事前分布は以下のように設定します.特に,$\alpha_i$はユーザー個別に推定しているため,階層的な事前分布を仮定します.
\begin{align*}
\alpha_i &\sim \mathcal{N}(\mu_\alpha, \sigma_\alpha) \\
\mu_\alpha &\sim \mathcal{N}(0, 10) \\
\sigma_\alpha &\sim \mathcal{C}_+(10) \\
\lambda_j &\sim \mathcal{B}(1, 1) \\
\tau_j &\sim \mathcal{N}(0, 10) \\
\end{align*}
ここで,$\mathcal{N}(\mu, \sigma)$は平均$\mu$標準偏差$\sigma$の正規分布,$\mathcal{C}_+(\sigma)$はスケール$\sigma$のコーシー分布を$0$以上で条件づけた半コーシー分布,$\mathcal{B}(a, b)$はパラメータ$a, b$のベータ分布です.
実装
上記のモデルをStanで実装したコードが以下です.
data {
int<lower=1> N; // number of users
int<lower=1> T; // time length
int<lower=1> J; // number of policies
array[N, T] int<lower=0, upper=1> y; // CV flag
array[N, T, J] int<lower=0, upper=1> x; // contact flag
}
parameters {
vector[N] alpha;
real mu_alpha;
real<lower=0> sigma_alpha;
vector[J] tau;
vector<lower=0, upper=1>[J] lambda;
}
model {
// priors
mu_alpha ~ normal(0, 10);
sigma_alpha ~ cauchy(0, 10); // half-Cauchy
alpha ~ normal(mu_alpha, sigma_alpha);
lambda ~ beta(1, 1);
tau ~ normal(0, 10);
// likelihood
for (i in 1:N) {
vector[J] a = rep_vector(0.0, J);
for (t in 1:T) {
for (j in 1:J) {
a[j] = x[i, t, j] + lambda[j] * a[j];
}
y[i, t] ~ bernoulli_logit(alpha[i] + dot_product(tau, a));
}
}
}
ダミーデータでの推定結果
ダミーデータを使って推定精度を調べます.ダミーデータにおける設定と真値は以下です.
- ユーザー数$N$:500
- 時点数$T$:50
- 施策種類数$J$:3
- 施策に接触したフラグ$x$:$5%$の確率でベルヌーイ分布から生成
- $\alpha$:$\mathcal{N}(-2, 1)$から生成
- $\tau$:それぞれ$2.0, 1.0, 0.5$
- $\lambda$:それぞれ$0.7, 0.8, 0.9$
以下はダミーデータを生成して,Stanでサンプリングを回すコードです.
import numpy as np
from cmdstanpy import CmdStanModel
# =========================
# ダミーデータ生成
# =========================
N, T, J = 500, 50, 3
rng = np.random.default_rng(0)
x = rng.binomial(1, 0.05, size=(N, T, J)).astype(int)
true_alpha = - 2.0 + np.random.randn(N)
true_tau = np.array([2.0, 1.0, 0.5])
true_lambda = np.array([0.7, 0.8, 0.9])
a = np.zeros((N, J))
z = np.zeros((N, T))
for t in range(T):
a = x[:, t, :] + true_lambda * a
z[:, t] = true_alpha + (a * true_tau).sum(axis=1)
p = 1 / (1 + np.exp(-z))
y = rng.binomial(1, p).astype(int)
# =========================
# 事後分布からのサンプリング
# =========================
model = CmdStanModel(stan_file="adstock.stan") # Stanファイルのパスを指定
data = {
"N": N, # ユーザー数
"T": T, # 時点数
"J": J, # 施策種類数
"y": y, # CVフラグ
"x": x # 施策に接触したフラグ
}
fit = model.sample(
data=data,
chains=4,
iter_warmup=1000,
iter_sampling=1000,
seed=123,
)
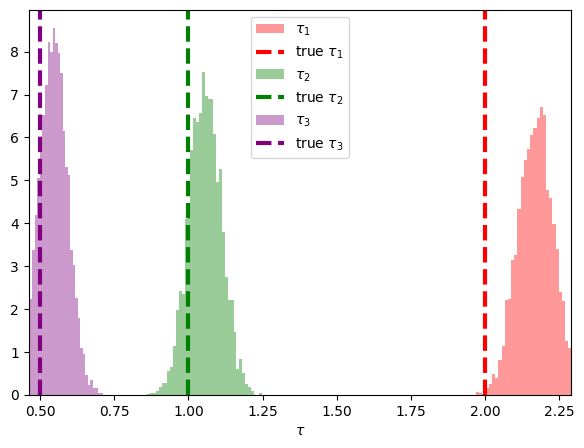
下のプロットは$\lambda$と$\tau$の事後分布からのサンプル(ヒストグラム)と真値(縦線)です.
ややバイアスはあるものの悪くない精度で推定できています.

また,下のプロットはランダムに選んだ3人のユーザーのCV確率の推移です.
施策に接触したタイミングとCVタイミングを縦線で示しています.
施策接触後にCV確率が上昇し,その後減衰し,蓄積していく様子が分かると思います.
まとめと発展余地
複数施策が走っている状況において,施策効果の減衰と蓄積を推定できるベイズ的なモデルを説明しました.
このモデルには以下のような発展の方向性がありうると考えています.
- ユーザーごとに異なる時間の長さを扱えるようにする:これはほぼ実装上の問題で自明な拡張です
- 連続値やカウントデータにも対応できるようにする:これも自明な拡張です
- 効果の減衰のモデリングを変える
- 効果の蓄積のモデリングを変える:MMMのパッケージのように施策効果の蓄積がサチるというモデリングもありかもしれません
- 施策効果$\tau_j$の異質性を考える:$\tau_j$にも階層的な事前分布をおくことで異質性を考慮できるはずです
- 施策の減衰速度$\lambda_j$の異質性を考える:上と同様です
※$\tau$を因果効果として解釈するのは注意が必要です.なぜなら,$\tau$はあくまで「過去に施策に接触した人のCV確率をどれぐらい引き上げたか」の推定値であり,別のターゲット層に施策をうったケースや無理やり接触率を上げたケースに外挿できるとは限らないからです.