概要
海外ではエンジニアの面接においてコーディングテストというものが行われるらしく、多くの場合、特定の関数やクラスをお題に沿って実装するという物がメインである。
その対策としてLeetCodeなるサイトで対策を行うようだ。
早い話が本場でも行われているようなコーディングテストに耐えうるようなアルゴリズム力を鍛えるサイト。
せっかくだし人並みのアルゴリズム力くらいは持っておいた方がいいだろうということで不定期に問題を解いてその時に考えたやり方をメモ的に書いていこうかと思います。
基本的にeasyのacceptanceが高い順から解いていこうかと思います。
前回
ゼロから始めるLeetCode Day3 「1313. Decompress Run-Length Encoded List」
問題
BSTとはBinary search tree、つまり二分探索木のことです。
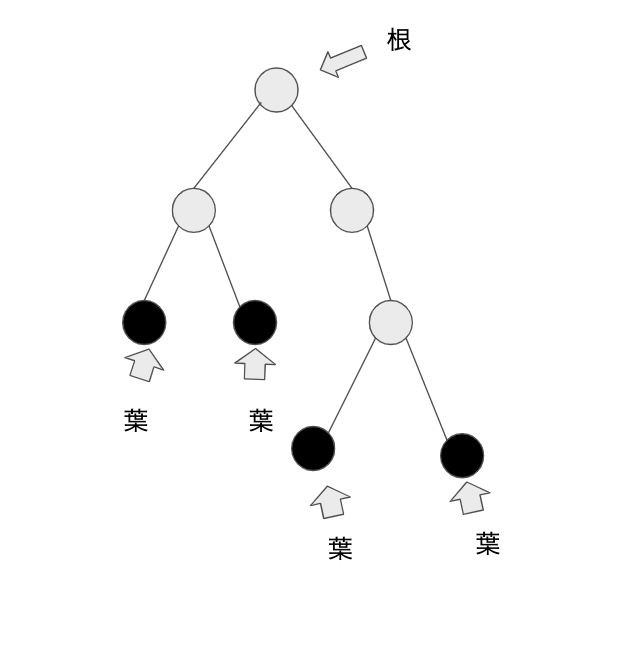
木の概念を知らないor曖昧な人もいると思うので、軽く説明しておくと、木は以下のような一つの「根」の下に複数の子ノードがぶら下がる形で階層構造を作り上げているデータ構造の考え方の一つです。子を持たない末端のノードのことを葉と言います。
根を起点として中間ノードを経由し該当のデータにアクセスするという過程で実行されます。
また、一定のルールをもとに木を構築することで中間ノードにインデックスの役割を持たせることもでき、特定の要素へのアクセスを効率化させることが出来ます。
実装方法としては配列かセルをポインタでつなげたものが考えられますが、一般的なものとしては要素数の変化に対応するためにセルをポインタでつなげたものが使用されます。
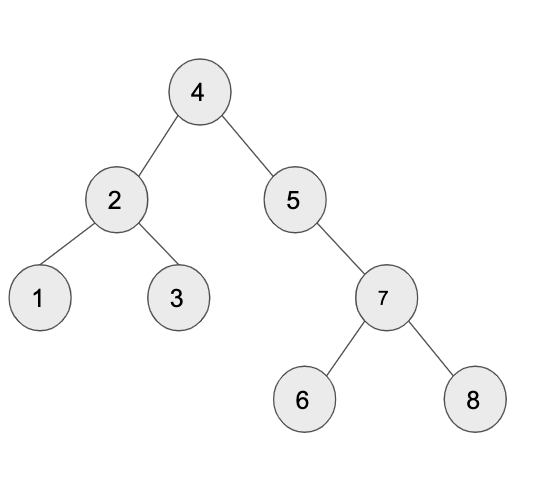
なお、この問題で触れられる二分探索木とは以下のようなものをイメージしてください。
ご覧いただけばすぐに分かると思いますが、左の子孫はすべて右の親よりも小さく、右の子孫は全て親ノードよりも大きくなっています。
この状況であれば、要素を取り出す際には該当するデータを根から順に親要素より大きいか小さいかで判断すればよく、その上要素を追加するときにも同様の処理を行うことでどこに新しいノードを追加するかがわかりやすい、というメリットがあります。
なお、要素を削除する際には、削除した後に穴を埋めるために子が一つであればそのままその要素を穴に入れ、二つあった場合にはより小さい方を穴に入れるという処理が必要です。
ここまでが木と二分探索木の構造の話です。それでは問題に移りましょう。
どうやらrootという名前の二分探索木が与えられるので、LとR、つまり左側と右側のノードを含む間の全てのノードの総和を返すような関数を作ることが目的のようです。
なお、全ての値はユニークなものであるという制約があります。
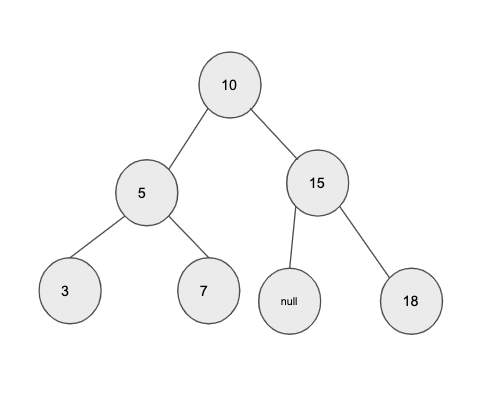
図で考えた方がわかりやすいと思ったので与えられている例を使って図を作りました。
root = [10,5,15,3,7,null,18], L = 7, R = 15
例1の与えられている条件をもとに二分探索木を作るとこのようになり、ここで求められる総和はL=7、R=15とあるので、7+10+15=32となります。
ここで注意すべきなのは、5を含めないという点です。確かにノードを順に追っていけば5は通るのですが、あくまでL=7,R=15の間に含まれる値の総和なので、5は含みません。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def rangeSumBST(self, root: TreeNode, L: int, R: int) -> int:
def dfs(node):
if node:
if L <= node.val <= R:
self.ans += node.val
if L < node.val:
dfs(node.left)
if R > node.val:
dfs(node.right)
self.ans = 0
dfs(root)
return self.ans
# Runtime: 224 ms, faster than 82.22% of Python3 online submissions for Range Sum of BST.
# Memory Usage: 21.9 MB, less than 7.92% of Python3 online submissions for Range Sum of BST.
考え方としては与えられたnodeの値がある間、LとRの値とnodeの値を比較し、L<= node.value <= Rの場合は総和にプラスし、それ以外の場合、Lよりnode.valueが大きい場合は左のnodeへ移り、Rよりnode.valueが小さい場合は右のnodeへと移る関数dfs(depth first search:深さ優先探索)を実装し、そちらを使って総和を出すという方式です。
深さ優先探索とは節点から節点へと辺の接続関係にしたがって子や孫へと再起的に探索を行うものであり、以下の記事で非常に分かりやすく解説されています。
DFS (深さ優先探索) 超入門! 〜 グラフ・アルゴリズムの世界への入口 〜【前編】
なお、他にある考え方としては、再起を使ったものがあります。
分かりやすい例がこちらです。
def rangeSumBST(self, root: TreeNode, L: int, R: int) -> int:
if not root:
return 0
elif root.val < L:
return self.rangeSumBST(root.right, L, R)
elif root.val > R:
return self.rangeSumBST(root.left, L, R)
return root.val + self.rangeSumBST(root.left, L, R) + self.rangeSumBST(root.right, L, R)
# Runtime: 244 ms, faster than 47.97% of Python3 online submissions for Range Sum of BST.
# Memory Usage: 22.1 MB, less than 5.94% of Python3 online submissions for Range Sum of BST.
今回の問題は木の構造と二分探索木、そしてdfsの例として非常に考えやすいため、試しに実装してみることをお勧めします。