安定感をあげるABCの「早解き」戦術

この記事は 競プロ Advent Calendar 2021 20日目の記事です。

拝啓 AtCoder黄色になりました

こんにちは。KowerKointと申します。
私は(受験生だったこともあり)水と青の境界付近で1年ほど停滞していましたが、2021年5月ごろからレートが一気に伸び始め半年で黄色に達することができました。これは色変記事ではないので自分のことを多く書くつもりはありませんが、入黄するにあたって新たに覚えた知識がほとんどあったわけではなく、ABCを安定させる(激冷えをしない)ことがもっとも有効だったと考えています。
ここでは、ABCでの順位を安定させあまり冷やさないようにするための早解きの技術をいくつか紹介します。

早解きすると嬉しいこと

早解きができると以下のメリットが発生します。

• 難問に挑戦する時間が増える
• 難問が解けなくてもレートが冷えにくくなる

前者は説明はいらないと思います。

後者について、あなたにとってA~Eは数分の考察でACできる問題で、F問題が「よく考えてうまくハマれば解ける問題」だったとします(つまり自分のレートと同じくらいのDiffです)。
全員前から順番にACしていると仮定すると、A~Eの5完で最速の人とFを時間ギリギリでACした人はほぼ順位が同じになります。
つまり自分にとって余裕な問題を最速クラスで解くことができれば、その後のチャレンジングな問題が解けなくてもそう痛くはないわけです。

本記事では解ける問題を他の人より早く解くための技術を環境面、実装面の2つに分けて紹介します。

時間がない人へ

実装面の最初の項だけでも見ていってください！！！

環境面での「早解き」戦術

エディタ・キーボード

※この節は沼であり様々な宗教が絡むため、私の考えを参考程度に見るくらいでいいかもしれません。

早解きのためには、思いついたコードを思いついた速度で入力する必要があります。
そのためにはVSCode等の多機能エディタが必須になります。
多機能エディタを使うことで書きかけの関数名や変数名をTabで補完したり、関数の引数に何を入れればいいかみながら入力したり、コンパイルが通らない箇所を先に警告してもらったりすることができます。
AtCoderのコードテストを使うより遥かに楽にコーディングができます。

プログラミングにおけるタイピングでは数字や記号を高速で入力できることが重要になります。
これは多くの問題を解いている間に自然と身につくと思うので説明はしません。
それだけを練習する必要もありません。

また、多くの場合カーソルの後ろにコードを書いていくだけで一発でコードで書くことはできません。
コーディング中には自動で補完された閉じ括弧の後ろに移動するような小さい移動や、グローバルな変数や関数を定義したくてコードの上の方にジャンプして元の場所に戻ると行った大きい移動が伴います。

小さい移動はキーボードのカーソルキーやHome/Endキーをうまく活用することで解決できるかも知れません。
この時ホームポジション上でカーソルキーやHome/Endキーを使えるような環境にあると嬉しいです。
例えば私はHappy Hacking Keyboard Professional Hybrid Type-Sの英語配列を使っていて、独自のキーバインドでホームポジション上からこれらのキーを使えるようにしています。
特別なキーボードを使わなくても同じようなキーマップを使うためにWindowsならAutoHotKeyが使えたり、macOSならデフォルトでEmacsのようなキーバインドが使えたりします。

大きい移動はエディタの機能に頼るしかありません。1〜3単語通しのユニークな文字列が行き先にある場合、積極的にCtrl+Fを使って検索しましょう。

小さい移動、大きい移動や編集をキーボードのみの多種多様なコマンドで行うことができるVimは私的には最強です。
私はNeovimをVSCodeのバックで実行してNeovimのキーバインドや拡張機能を使えるvscode-neovimを導入して使っていますが、Vimのキーバインドはかなりクセがあり、習得に時間がかかるので競プロだけのために勉強することはおすすめしません。

ライブラリ

ライブラリ整備もかなりの重要項目です。
競プロではセグメント木など、多くの言語のSTLに存在しない汎用関数やデータ構造が登場します。
遅延評価セグメント木やDinic法などは特にそれを書くだけで時間がかかり、余計なバグを生みやすいです。
このようなものはライブラリ化していつでも提出コードに含めることができるようにしておくべきです。
僕は自力で書いたライブラリを持っておらず、個人的に信用している2つのライブラリを常用しています。

AC Library

ACLはAtCoder上ならincludeを書くだけで使うことができる公式のC++ライブラリです。
公式なので当然使用者が多く、ACLを使うだけのような問題はこれが出る以前に比べて特に正解者数が多くなる傾向がみられます。
他言語使用などの理由でACLを使わない場合でもACL使用者と同等の速度でこの内容が用意できるよう必ず気にかけておきましょう。

これは余談ですが、順位表をみて短い時間で通してる人が多い場合ACLを貼るだけの問題である可能性を疑ってもいいかも知れません。

Luzhiled's Library

ei1333さんが管理しているライブラリです。(名前についてはややこしいので言及しないでおきます)
ACLに比べてとにかく量が多いです。
私は整数論に関する諸関数(素数列挙や素因数分解など)のコーディングをサボったりグラフのよくわかってないアルゴリズムを取り敢えず雑に貼ってその場を凌ぐ目的で使っています。
チェックが行われているものが多いですが、非公式のライブラリなので間違っていても当然AtCoderには保証されません。

テンプレート

多くの言語は競プロ用に最適化されていません。
例えばC++ではincludeとmain関数以外に何も書かなければstd::を至るところにつけたり、longの大きさが環境によって異なっていたりと困ることがたくさんあります。
競プロをやる上で常にコードに入っていると嬉しいものは先に書いておいておくといいです。

C++(gcc)では下記の宣言は多くの人が先にやっています。

#include <bits/stdc++.h>
using namespace std;

<bits/stdc++.h>の中には大量のinclude文が入っており、STLについては基本的に全て追加のincludeをせずに使えるようになります。
using namespace std;を書くことでstd名前空間に属する大量の宣言を、std名前空間の指定なしに書くことができます(例えばstd::coutを単にcoutと省略できるようになります)。

この他にも個人的に簡単で便利だと思ういくつかのC++テンプレートを紹介します。

using ll = long long;
using VI = vector<int>;
using P = pair<int, int>;

型エイリアスです。
ここに上げているのは一例に過ぎませんが、長い型名やテンプレート引数を取る型名でよく使うものはこのように短い名前のエイリアスを宣言しておくと楽になります。

#define REP(i, n) for(int i = 0; i < (int)(n); i++)
#define FOR(i, a, b) for(ll i = a; i < (ll)(b); i++)
#define ALL(a) (a).begin(),(a).end()

マクロです。

REPマクロは特に有名で、0からnまでの半開区間を取るループ変数とともにn周のfor文を回します。

ALLマクロは、std::sort()などにコレクション(std::vectorなど)の全範囲を渡す際に便利なマクロです。
lower_bound(v.begin(), v.end(), x)をlower_bound(ALL(v), x)と書くことができます。

これらのマクロには単にコードを短く書くだけの目的でなく、変数ミスを減らす目的もあります。
for(int i = 0; i < n; i++)をfor(int j = 0; j < n; j++)と書き換えたくなった場合、通常3箇所書き換える必要があるのところがREPマクロを使っていれば1箇所書き換えるだけでよくなるので、ミスを減らしたりデバッグにかかる時間を短縮したりすることができます。
これも早解きのためのコツの1つです。

constexpr int INF = 1001001001;
constexpr ll LINF = 1001001001001001001ll;
constexpr int DX[] = {1, 0, -1, 0};
constexpr int DY[] = {0, 1, 0, -1};

定数です。
INFは非常に大きい数として使います。1001001001を採用している理由についてはいくつかあって、

• 自身との和をとってもINT_MAXまで余裕がある(最短経路問題の実装等でmin(INF, INF + INF)のような計算になることがあってもオーバーフローしない)
• 3桁ごとに1が並ぶので桁数を数えやすい
• わかりやすい見た目なのでデバッグ出力した時にINFやそれにいくらか足し引きした値であることがわかりやすい

といったものです。
他の数(1000000000とか)を採用してもいいと思います。

DX、DYはグリッド探索に使う値です。
現在座標(x,y)にいるときに

REP(i, 4) {
    int nx = x + DX[i];
    int ny = y + DY[i];
    // ここになにか処理
}

と書くと上下左右4方向に隣接する座標についての処理が簡単に書けます。

if(nx < 0 || nx >= h || ny < 0 || ny >= w) continue;

と続けて書くことが多いです。(早期にcontinueやreturnすることも例外的なケースを考えなくて済むようにするための有効なテクニックです)

template< typename T1, typename T2 >
inline bool chmax(T1 &a, T2 b) { return a < b && (a = b, true); }

template< typename T1, typename T2 >
inline bool chmin(T1 &a, T2 b) { return a > b && (a = b, true); }

よくあるやつです。最小値・最大値を更新します。かなりうれしい。

void print() { cout << '\n'; }
template<typename T>
void print(const T &t) { cout << t << '\n'; }
template<typename Head, typename... Tail>
void print(const Head &head, const Tail &... tail) {
    cout << head << ' ';
    print(tail...);
}

これはややトリッキーな関数です。
ここでは詳しい説明を省きますが、Pythonのprint()と同じことをC++でもできるようにしています。
つまり、0個以上の可変長な引数を取って、それらを空白区切りで標準出力に流した後改行します。

これに関連して以下のマクロを定義すると便利です。

#define END(...) { print(__VA_ARGS__); return; }

END()の中身を改行付きで出力してreturnします。
私は解答をvoid solve()という関数の中に書くようにしているのでreturnとしていますが、main()に直書きしている人は変わりにreturn 0とするといいと思います。
特殊なケースで答えが早く決まった/考察から早く取り除きたい場合は先に出力してプログラムを終了してしまえばいいという発想です。
ちなみに{}を使っているせいで中括弧なしのifにEND(a);の形で書くと後ろにelseがつけられなくなるといった注意点があります。

template< typename T >
ostream &operator<<(ostream &os, const vector< T > &v) {
    for(int i = 0; i < (int) v.size(); i++) {
    os << v[i] << (i + 1 != (int) v.size() ? " " : "");
    }
    return os;
}

template< typename T >
istream &operator>>(istream &is, vector< T > &v) {
    for(T &in : v) is >> in;
    return is;
}

vectorをそのままcin/coutするためのテンプレートです。

//n要素の配列に一気に入力
vector<int> a(n); cin >> a;

//多次元配列もそのまま入ります
vector<vector<int>> a(n, vector<int>(m)); cin >> a;

このようにサイズが先に決まってれば正しくcinできます。

私はこの他にもいくつか便利テンプレートを採用しています。(筆者のヘッダ(随時更新中))
みなさんもお気に入りのテンプレートをバリバリ書いていきましょう。

自動テスト・提出

AtCoderのコンテストページは特定のシンプルなフォーマットに従っているため、プログラムによってサンプル入出力を自動で取得したり解答ソースを提出したりすることができます。

特に有名なのがatcoder-cliやonline-judge-toolsです。
atcoder-cliについては私はよく知りませんが、online-judge-tools(oj)は拡張ツールのverificaton-helperなどによってサンプルの取得・自動テスト・提出以外にもincludeしたライブラリの提出時自動展開等の機能をもたせることができ、大変便利です。

私はojの操作をVSCodeのタスクとして実行できるCompPro-Workspaceを主に使っていますが、近々これのVim版を作りたいと思っています。
このような自動化ツールを自作するのも面白いと思います。

2022/05/31追記
Vimに対応したりいろいろ自作ライブラリを使えるようにしたり色々改変して今はCompPro-CLIを使っています。

実装面での「早解き」戦術

解法がわかってもコードが長くなる実装やデバッグしにくい実装は大きなタイムロスに繋がります。

• 同じような長いルーチンを「コピペ→少し修正」で2度書いている
• 条件分岐が無駄に多い
• ブロックが無駄に深い

などは、修正ミス(一部変数名の変え忘れなど)のリスクが大きかったり編集時のカーソルの大移動などが多くなったりして好ましくありません。
早解きのためだけでなく簡単な問題を安定的に解くためにスマートなコードを書くよう（最初は一度立ち止まってでも）考えて実装すると良いと思います。

ここで紹介するテクニックより先に、E8さんの実装記事の中に新発見があるなら先にそちらを習得したほうがいいと思います。そのうえで私流の実装テクを追加する形で紹介します。

コピペの変わりにループを使う

早速私が最も伝えたいテクニックです。

AGC008 Aを題材にして解説します。
問題の概要は以下です。

• 整数$X$、$Y$が与えられる
• 以下の操作のいずれかを0回以上行い、$X$を$Y$に一致させる
  • $X$を1増やす
  • $X$の符号を反転させる
• 操作回数の最小値を求めよ

符号反転は最初と最後以外でやっても改善しないので、この問題は$X$と$Y$それぞれの符号を反転させるかどうかを選んだ4通りの中で$X\leq Y$となるケースの$Y-X$の最小値を求めることでACできます。

C++での一般的な解法として以下のコードを考えます。

#include <bits/stdc++.h>
using namespace std;

int main() {
    int x, y; cin >> x >> y;
    int ans = 1 << 30;
    if(x <= y) ans = min(ans, y - x);
    if(-x <= y) ans = min(ans, y + x + 1);
    if(x <= -y) ans = min(ans, -y - x + 1);
    if(-x <= -y) ans = min(ans, -y + x + 2);
    cout << ans << '\n';
}

これくらいの問題なら十分短いコードになりますが、同じような条件分岐と答えの修正が2度行われているため実装時にミスが起こりやすいです。
そこで、ループによってxとyの反転を自由にしながら行うことにします。以下のようになります。

#include <bits/stdc++.h>
#define REP(i, n) for(int i = 0; i < (int)(n); i++)
using namespace std;

int main() {
    int x, y; cin >> x >> y;
    int ans = 1 << 30;
    REP(_x, 2) {
        REP(_y, 2) {
            if(x <= y) ans = min(ans, y - x + _x + _y);
            y = -y;
        }
        x = -x;
    }
    cout << ans << '\n';
}

解答のための主なルーチンを1回で済ませることができました。
ここでは_xと_yの2周ループの最後でxとyそれぞれの符号を反転しています。
_x、_yがそれぞれ1の時にx、yが反転している状態になります。
なお反転は2回行われるのでこの処理が終わったときにはxもyももとの状態に戻っています。

「2回やってもとに戻る」操作の典型は符号反転以外にswapなどもあります。

// a,bについてそれぞれ同じ処理を行いたい
REP(_, 2) {
    // ここにaに適用する処理を書く

    swap(a, b)
}

このような書き方をすることで、「コードをコピペ→a,bの変数名を書き換え」をする余計な動作をせずに済みます。

状況は少し異なりますがTenka1 Programmer Beginner Contest Bは以下のようなコードでACできます。

#include <bits/stdc++.h>
#define REP(i, n) for(int i = 0; i < (int)(n); i++)
using namespace std;

int main() {
    int a, b, k; cin >> a >> b >> k;
    REP(i, k) {
        b += a / 2;
        a /= 2;
        swap(a, b);
    }
    if(k % 2) swap(a, b);
    cout << a << ' ' << b << '\n';
}

偶数・奇数ラウンドで動作の対象が反転する典型的な例ですが、ループの最後にswapすることでこのようにスッキリ書くことができます。

とりあえず配列で持っておく

配列は大変有用な構造です（知ってる）。
配列で管理しなくても良いような情報でも、配列で持っておいたほうが楽な場合が多々あります。

例えばABC028 Cは、A,B,C,D,Eというふうに入力が与えられていますが、これらには均等意味付けがされており、1つの配列として持つほうが圧倒的に計算しやすいです。

#include <bits/stdc++.h>
#define REP(i, n) for(int i = 0; i < (int)(n); i++)
using namespace std;

int main() {
    vector<int> a(5);
    REP(i, 5) cin >> a[i];
    vector<int> sum;
    REP(i, 5) REP(j, i) REP(k, j) {
        sum.push_back(a[i] + a[j] + a[k]);
    }
    sort(sum.begin(), sum.end(), greater<int>());
    cout << sum[2] << '\n';
}

別の例としてグリッド探索があります。
PAST3 Gを例に挙げます。
BFSでグリッド迷路を探索する問題で、1回の移動で点$(x,y)$から

• $(x+1,y+1)$
• $(x,y+1)$
• $(x−1,y+1)$
• $(x+1,y)$
• $(x−1,y)$
• $(x,y−1)$

の6方向に移動することができるという制約です。
この問題で各移動について「移動可能か判定してQueueにPush」を試していると、同じようなコードが6回書かれることになってしまいます。
この場合移動方向を先に配列で持っておくと簡単になります。
私の解答がこちらです。

#include <bits/stdc++.h>
#define REP(i, n) for(int i = 0; i < (int)(n); i++)
using namespace std;

int main() {
    int n, gx, gy; cin >> n >> gx >> gy;
    set<pair<int, int>> blocks;
    REP(i, n) {
        int x, y; cin >> x >> y;
        blocks.emplace(x, y);
    }
    int dx[] = {1, 0, -1, 1, -1, 0};
    int dy[] = {1, 1, 1, 0, 0, -1};
    queue<pair<int, int>> que;
    map<pair<int, int>, int> dist;
    que.emplace(0, 0);
    dist[{0, 0}] = 0;
    while(!que.empty()) {
        auto [x, y] = que.front(); que.pop();
        REP(i, 6) {
            int nx = x + dx[i], ny = y + dy[i];
            if(nx < -201 || nx > 201 || ny < -201 || ny > 201) continue;
            if(dist.count({nx, ny})) continue;
            if(blocks.count({nx, ny})) continue;
            if(nx == gx && ny == gy) {
                cout << dist[{x, y}] + 1 << '\n';
                return 0;
            }
            dist[{nx, ny}] = dist[{x, y}] + 1;
            que.emplace(nx, ny);
        }
    }
    cout << "-1\n";
}

注目すべきは

    int dx[] = {1, 0, -1, 1, -1, 0};
    int dy[] = {1, 1, 1, 0, 0, -1};

の部分で、$0\leq i\lt 6$についてx,yにdx[i],dy[i]を足すことで各移動先に移動できます。
このコードにはもう1つの重要テクニック「早期にcontinue、returnをする」ということが含まれています。

if(nx < -201 || nx > 201 || ny < -201 || ny > 201) continue;

は調べる必要のないマスに来たら処理を飛ばすために書いています。
また、答えが決まった時点で早々に出力してreturnしているのもその先のことを考えなくて済むようにするためです。

min、maxを積極的に使う

std::min()、std::max()は単純ですが大変有用な関数です。
答えに下限・上限があるときにそれを越さないように丸めることができます。

まずは単純な例から。
ABC204 Bを考えます。
この問題では

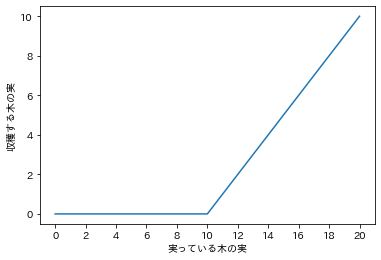
• 実っている木の実が10個以下の木からは木の実を収穫しない
• 実っている木の実が10個より多い木からは、10個を残して残りの全てを収穫する

という2つの場合によって収穫する木の実の個数が変わります。
この2つの条件に対する解答は連続しているので1つの式で表すことができます。

上のグラフは実っている木の実と収穫する木の実の対応を表したグラフです。
$x=10$の部分で折れ曲がっていることがわかります。
このようなときは斜めの方をメインに考えます。
つまり主に出力すべきは$x-10$ですが、答えは$0$より小さくはなりません。
下限は0ですから、max(0, x - 10)とするといいことがわかります。

このように下限が決まっているときはmax(下限, 本来の値)、上限が決まっているときはmin(上限, 本来の値)とすることで条件分岐のない簡潔なコードになる場合があります。

#include <bits/stdc++.h>
#define REP(i, n) for(int i = 0; i < (int)(n); i++)
using namespace std;

int main() {
    int n; cin >> n;
    int ans = 0;
    REP(i, n) {
        int a; cin >> a;
        ans += max(0, a - 10);
    }
    cout << ans << '\n';
}

少し異なる例を考えます。
ARC107 Bを考察します。
これは

• $1≤a,b,c,d≤N$
• $a+b−c−d=K$

を満たす整数の組$(a,b,c,d)$が何通りあるかを求める問題です。
ここでは考察を楽にするため1つ目の条件を$0≤a,b,c,d≤N-1$と言い換えても変わらないことを利用します（下限を$0$にするといいことがよくあります）。

$(a+b)$と$(c+d)$をまとめて考えることにして、$(a+b)-(c+d)=K$であるような$(a+b),(c+d)$についてそれぞれ$(a,b),(c,d)$の振り方が何通りあるかを考えます。

$0\leq(a+b)\leq 2(n-1)$を満たすのでその範囲で$(a+b)$を全探索し、$(c+d)=k-(a+b)$から$(c+d)$を求めます。
まず$0\leq(c+d)\leq 2(n-1)$を満たさない場合はさっさとcontinueして考察から除外します。

次に$(a+b)$が決まっているときの$a,b$の割り振り方ですが、

$(a+b)=k$が小さいときは$0\leq a \leq k$(上限)なる$a$に対して有効な$b$が存在して$k+1$通りになります。
$(a+b)=k$が大きいときは下限$\leq a \leq n-1$の形の範囲が条件を満たすことが直感的にわかると思います。
この下限はわざわざ計算しなくても$k$が小さいときと「対称」な位置に来ることがわかれば、全体としての場合の数は$k$が小さい場合の$k$を$2(n-1)$に置換したものであることが素早く想像できます。

この2つの場合において、全体の場合の数としては「より厳しいほう」が採用されることになりますから、min(ab, (n-1)*2 - ab) + 1と一発で書けばすべて解決します。

#include <bits/stdc++.h>
#define REP(i, n) for(int i = 0; i < (int)(n); i++)
using namespace std;
using ll = long long;

int main() {
    ll n, k; cin >> n >> k;
    ll ans = 0;
    for(ll ab = 0; ab <= (n - 1) * 2; ab++) {
        ll cd = ab - k;
        if(cd < 0 || cd > (n - 1) * 2) continue;
        ans += (min(ab, (n-1)*2 - ab) + 1) * (min(cd, (n-1)*2 - cd) + 1);
    }
    cout << ans << '\n';
}

早期にcontinue、returnをする

ここまでたくさん用いてきましたから例を増やして解説をすることはしません。
ただ結果が決まったなら早くループや関数から抜け出して考察から除外する、というのは結構重要なことなので改めて書きました。
continueの条件の後にelseをつなげたってブロックが1段深くなって読みくいだけです。

ラムダ式を多用する

ここでいうラムダ式はC++のラムダ式のことです。
Python勢の方は関数内関数や、グローバルなコードの途中で定義する関数だと思ってください。

関数を多用するメリットについてはE8さんの実装記事で紹介されている通りなのですが、ここではC++のラムダ式が嬉しいことについて書きます。

ズバリ言って、競プロにおいてラムダ式を嬉しく感じるところは、関数外の変数を参照できることです。
例えば木DPで再帰関数を使ってDFSをしたいとき、通常のグローバル関数を使って実装するとグラフの隣接リストはグローバルに置くか引数として(もちろん参照で)渡すことになりますが、わざわざmain()の外にでてグローバルに書くというのは手間ですし管理が面倒です。
特に他の識別子と名前が衝突すると厄介ですよね。

そこで有効なのがラムダ式です。ラムダ式は関数の内部に書くことができ、外の変数を参照でキャプチャできるので大変便利です。
各頂点を根とする部分木のサイズを求める木DPでの実装を以下に示します。

#include <bits/stdc++.h>
#define REP(i, n) for(int i = 0; i < (int)(n); i++)
using namespace std;

int main() {
    int n; cin >> n;
    // 競プロでよくある入力を想定して隣接リストを作っています
    vector<vector<int>> graph(n);
    REP(i, n - 1) {
        int a, b; cin >> a >> b; a--; b--;
        graph[a].push_back(b);
        graph[b].push_back(a);
    }

    vector<int> sz(n); // DPテーブル(今回は部分木のサイズ)
    // ラムダ式でDFSを定義(型を省略できるけどややこしいので全部書き)
    function<void(int, int)> dfs = [&](int from, int par) -> void {
        sz[from] = 1;
        for(int to : graph[from]) {
            if(to == par) continue;
            dfs(to, from);
            sz[from] += sz[to];
        }
    };
    dfs(0, -1); // 実行するのよく忘れる
}

見るからに楽です。

2020/12/20 追記
ここでは簡単に再帰呼び出しを行うためにfunction型で宣言していますが、
function型は遅かったり再帰の深さ上限が落ちたりするらしいです。
詳しくはC++のラムダで再帰するを参照ください。
atreeさんご指摘ありがとうございます！

終わりに

ここまでたくさんの知識を提供してきましたがこんなにたくさんのこと一度に詰め込めるわけがありません。
何ならこのような早解きは知識のお勉強をするよりも経験を詰んだほうが絶対にいいと思います。

経験を積むには継続して(できれば毎日)バチャをやるのが理想です。
自分と同じDiffを解き重ねるのも大事ですが、それだけでうまく行かない人は低難易度を習慣的に解き続けることをおすすめします。

最後になりますが、AtCoder Problemsで私が毎日参加している「あさかつ」を紹介します。
あさかつは毎朝7:30~8:30に灰(50未満)、灰(50以上)、茶、緑、水、青の6問構成で行っているバチャで、記事執筆現在(2021/12)毎日約15人が参加しているバチャです。
朝の1時間をバチャに使ってもまだ午前中の活動には十分時間が残ります！
気軽にご参加ください。

あさかつに参加するのが時間的に厳しい方もTerryさんの「くじかつ」やmtsさんの「土日バチャ」等いくつか定期的なバチャがあります。
能動的に競プロを続けるのが難しいと思ったら習慣的してしまえばいいのではないでしょうか。

ここまで読んでいただきありがとうございました。
皆さんがABCを卒業して暖色に入るのを心待ちにしております。