【AtCoder】普通の人である私が緑になるまでにしたこと

こんにちは、Kotaです。
ご閲覧いただきありがとうございます！

昨日開催されましたAtCoder Beginner Contest 176でレーティングが緑になりました！

ついに！入緑しました！！！
ここまで長かったのでめちゃくちゃ嬉しい😄

kota0501さんのAtCoder Beginner Contest 176での成績：1754位
パフォーマンス：1241相当
レーティング：754→815 (+61) :)
Highestを更新し、6 級になりました！#AtCoder #ABC176 https://t.co/ONTPDcUzzV pic.twitter.com/jQKX7gwBsa

— Kota (@kota0501_orca) August 22, 2020

要約

• 競プロ開始してから7ヶ月弱で緑になったよ！
• この界隈は人外な人が多いよ！(人外についての説明は記事内で！)
• だから普通の人である私が緑になるまでにしたこと&していないことをまとめるよ！

1. はじめに

競技プログラミング(競プロ)は、2020年1月12日に初コンテストに出場し、そこから取り組んでいきました。
そして、始めてから昨日(2020年8月22日)のコンテストまでの7ヶ月弱で、レーティングが**緑(800-1199)**になりました。
この章で、レート感についてと、期間についてを所感として書いておきます。

レート感

緑レートのレベル感については、chokudaiさん(AtCoder社 社長)が以下のようにまとめてくれています。(2020年8月23日時点)

緑色　(Cランク R800~1199　上位30%)
緑色になれれば、「競技プログラミングに熱心に取り組んでいる人」と考えて問題ないでしょう。要求レベルも決して低くなく、出場回数が足りないとマイナス補正がかかるため、運だけで到達することはまず出来ないラインです。他社アルゴリズム力判定サービスだと、上位１％の最高ランクが付く実力です。（あくまで「アルゴリズム力部分だけであることに注意してください）

印象としては、

• 学生ならかなり優秀。

• エンジニアとしてもある程度の安心感がある。論理的に複雑な処理の実装に対応できない、なんてことはなさそう、くらいには思える。データ量が多い現場など、計算量の多い処理が要求される現場でなければ、このレート帯以上を求める必要はほぼない。

くらいの印象です。もちろんアルゴリズム力しか計ってないので個人差があります。

技術的な部分では、

• if、forはもちろん、それを組み合わせて2次元配列に対して操作をしたり、深さ優先探索や幅優先探索などのキューや再帰を使った実装も出来る。

• 簡単な動的計画法の問題や、数学的に工夫する問題など、計算量の工夫も出来始める。

という感じです。

AtCoder（競技プログラミング）の色・ランクと実力評価、問題例

このレベル感については、賛否両論あるようですが、今回は関係がないので割愛します。

このレベル感を見て、どう思うかは人によると思いますが、普通の人である私は、

「少しプログラミングはやったことあるし、競プロ自体に慣れればすぐに到達できそう！
if, for, 2次元配列って書いてあるし、そのくらいなら分かる！」

と思いました。(都合が良い部分だけを読み取った結果です。)

結論を言うと、この認識はかなり間違っていたと今は痛感しています。
上の認識だと、レート200-300(灰色)が良いところだと思います。

期間

競プロを開始してから緑になるまでの期間の7ヶ月弱についてですが、この界隈では決して早くはありません。

chokudaiさんが以下のように言及しているので「人外」というワードを使いますが、成長速度が異常な「人外」がとても多いです。

【競プロの各色に対する認識オススメ】
・２色上は人外だと思うのが大切！比較しちゃだめ！１色上に追いついたところで人間に戻してあげよう！
・１色上は強い人！目標にするのは良いけど勝てなくて当たり前！いつかは追いつけたらいいなくらいに思おう！
・同色でも成長がヤバいやつはやっぱり人外！

— chokudai(高橋 直大)🍆🎪🐦 (@chokudai) June 29, 2020

観測した範囲だけでこのような人外がいました。(人外度昇順)

• 1ヶ月で緑レート到達
• 半年で青レート到達
• 1回のコンテストで水レート到達

これらは人外度が高い人をピックアップしているのですが、これらとはインパクトが弱いものの十分に人外な人だらけです。
特にTwitterではこういった人が目立つため、「これが普通なのかー。」と最初は勘違いしてしまいます。
そして、どうしても比較していまい、「なんで自分は…。」と思うところまでがワンセットです。

そのため、普通の人である私が、一般的(?)な期間で緑レートになるまでにしたことと、連呼している私(普通の人)のスペックを書いていきます。

記事の構成

記事の構成はこのようになってます。
少し長いですが読んでいただけると嬉しいです！

1. はじめに
   2. レート感
   3. 期間
   4. 記事の構成
2. 普通の人である私のスペック
3. 緑になるまでにしたこと&していないこと
   1. 緑になるまでにしたこと
   2. 緑になるまでにしていないこと
4. 学んだアルゴリズムとデータ構造
5. 持ってるライブラリ
   6. 複数の数の最大公約数・最小公倍数
   8. 約数列挙
   9. 素因数分解
   10. MOD用組み合わせ
   11. Union-Find木
6. 使っているスニペット
7. おわりに
8. よく勉強に利用させていただいたサイト

2. 普通の人である私のスペック

前提として、普通の人というのは定量的に測れるものではありません。

しかし、

「普通の人？どうせよくいる強い人なのでは？」

と思われてしまうのも嫌なので簡単にですが、私のスペックを書きます。

• 新卒1年目のWebエンジニア(ここ2ヶ月間で書いたコードは0行)
• 地方国立大学学部卒
  • 高専からの3年次編入なのでセンター数学経験なし
• 基本情報技術者試験を取得
• データ分析用途でPythonは使ったことがある(AtCoderではPython(PyPy)を使用している)

要するに競プロで大事である、高校数学のちゃんとした勉強経験がないということです。
これを見てどう感じ取るかも人それぞれですが、競プロ界隈では間違いなく上位ではないです。
逆にプログラミング自体は高専に通っていたこともあり、早めに始めたことから、総合的にみて特段に低いとも思っていないため、普通の人と言わせてもらっています。

3. 緑になるまでにしたこと&していないこと

次に、そんな普通の人である私が緑レートになるまでにしたことを書いていきます。
また、していないことを書かれた記事がほぼなかったのでそちらも書きたいと思います。

3.1. 緑になるまでにしたこと

したことは次のようなことです。

• 毎日AC
• 高校数学の勉強
• Twitter

次からはこれらのしたことの詳細を書いていきます。

毎日AC

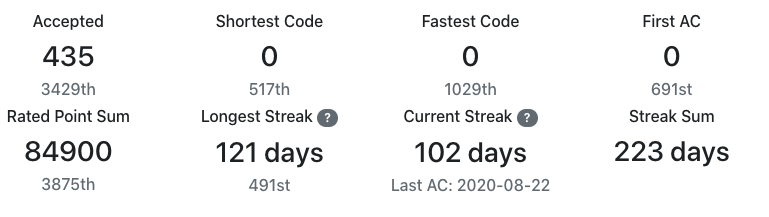
AtCoder ProblemsでStreakが見れるので毎日ACすることを日課にしてます。

簡単な問題を埋める、いわゆる虚無埋めをやってしまいがちなのですが、それでも解かない日があるよりかはましと思って解いてます。(習慣化することが大事！)

Current Streakは、Unique ACがカウント対象と知らずに途中で切れました。
違う解法で解き直したら見事に切れてしまいました。笑
みなさんも気をつけてください！

ここから記念にぺたぺた貼っていきます。

Achievement

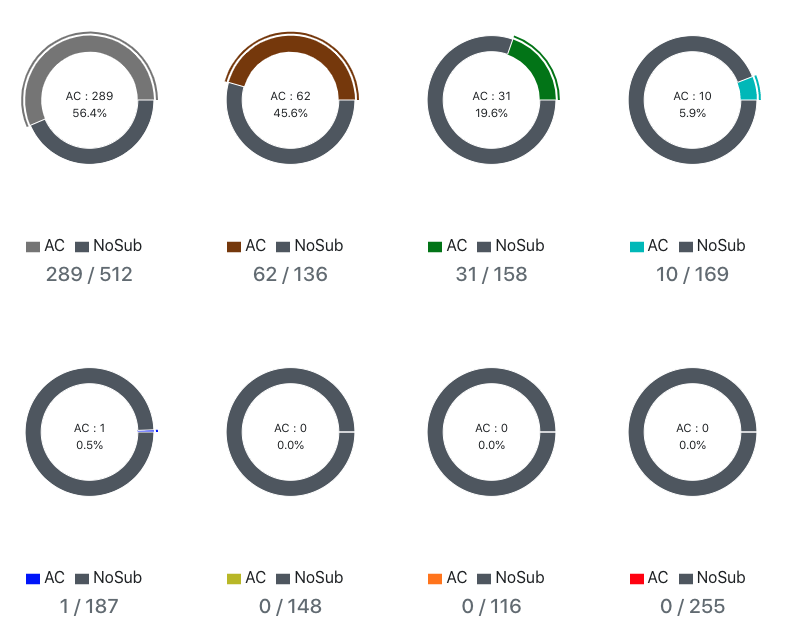
Difficulty Pies

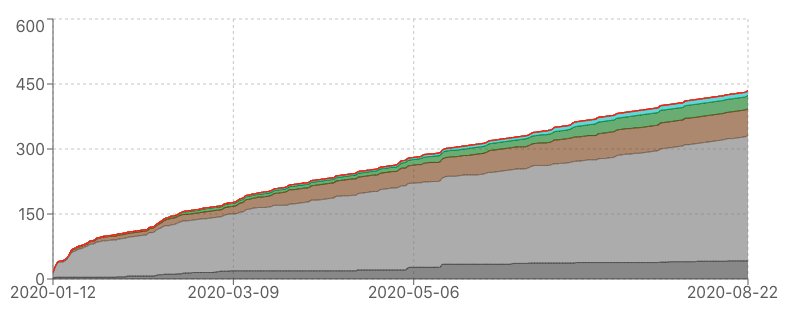
Climbing -Colored-

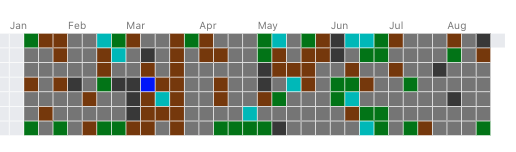
Heatmap -Max Difficulty-

あと、GitHubに競プロでUnique ACしたものを毎日定時に自動PUSHするようにしています。
精進によって草が生えていくため、モチベーションにもなるのでおすすめです！

高校数学の勉強

高校数学の美しい物語のサイトで勉強しました。

私的には難しいものが多いので飛ばし飛ばしで読んでいますが、様々な発見もあり面白いのでおすすめです。

これからも少しずつ読み進めていきたいと思います。

Twitter

競プロは継続、つまりモチベーション維持が大切です。
そのため、モチベーション維持のためにTwitterアカウントを作成するというのがよくなされています。

疑心暗鬼な気持ちで始めてみましたが大成功でした！

本界隈は、人外が多いのも事実なのですが、優しい人(⊇人外)がとても多いです。
様々なところで分からないところを教えあったり、励ましあったりしています。

人によるとは思いますが、一人で黙々と精進するよりかは誰かと一緒に精進した方が精神的にも良いためおすすめです！

私のTwitterアカウント

↑よければ、私のTwitterアカウントもフォローお願いします！一緒に精進していきましょう！

3.2. 緑になるまでにしていないこと

していないことは次のようなことです。

• 蟻本などの競プロ本購入
• バチャコン参加
• 外部コンテスト参加

次からはこれらのしていないことの詳細を書いていきます。

蟻本などの競プロ本購入

よく見るこの本のことです。

他にもchokudaiさんが著者のチーター本と呼ばれる競プロ本もあります。

アルゴリズムについての情報はネット上に有志の方がきれいにまとめてくださっているので購入していないです。
有志の方がまとめてくださっているよく勉強で使用させていただいたサイトについては、記事の最後でまとめています。
あと、私がPython(PyPy)を使用しているという理由もあります。(蟻本は参考実装がC++らしいので)

バチャコン参加

AtCoder Problemsでよくバチャコンと呼ばれるバーチャルコンテストが開催されています。

くじかつと呼ばれるものはほぼ毎日開催されているようです。

レーティングに反映されないこともあり、まとまった時間をとることが厳しいため参加していないです。

外部コンテスト参加

このCodeforcesという海外コンテストに参加されている方が多いです。

参加してみたいとは思っているのですが、海外のコンテストなので時間が不規則かつ健康的な時間に開催していないことが多いので避けてしまっています。

ただコンテストへの参加は、モチベーションを保つ上で大事なことだと感じているので、可能であれば積極的に参加した方が良いと思います。

4. 学んだアルゴリズムとデータ構造

学んだアルゴリズムとデータ構造について書いていきます。
また、学んだはいいものの緑になる上でコンテストでは使わなかったものは明記したいと思います。
そして、その上で緑になる上での重要度を独断と偏見で書きます！

名前	使った(○)・使っていない(×)	重要度(高・中・低)
bit全探索	○	高
二分探索	○	高
累積和	○	高
約数全列挙	○	高
素因数分解	○	高
GCD・LCM	○	高
貪欲法	○	中
幅優先探索(BFS)	×	中
深さ優先探索(DFS)	×	中
imos法	×	低
動的計画法(DP)	×	低
優先度付きキュー	×	低
グラフアルゴリズム	×	低
ダブリング	×	低
Union-Find Tree	×	低

こう見ると必要なのは、典型的なアルゴリズムスキルより、素早く正確な考察力だと分かります。
もちろん様々なアルゴリズムを使いこなせた方が良いのは間違いないと思いますが、緑になるだけならそこまで多くのアルゴリズムを学ばなくても良さそうです。

5. 持ってるライブラリ

ライブラリというまでのものではありませんが、保存しているものを貼っておきます。
よく使うものは、すぐにコピペできるところに置いておくのが良いと思ってます！

複数の数の最大公約数・最小公倍数

from functools import reduce

# 最大公約数
def gcd_list(num_list: list) -> int:
    return reduce(gcd, num_list)

# 最小公倍数
def lcm_base(x: int, y: int) -> int:
    return (x * y) // gcd(x, y)
def lcm_list(num_list: list):
    return reduce(lcm_base, num_list, 1)

約数列挙

def make_divisors(n: int) -> list:
    return_list = []
    for i in range(1, int(n**0.5)+1):
        if n % i == 0:
            return_list.append(i)
            if i != n // i:
                return_list.append(n//i)

    return return_list

素因数分解

def prime_factorize(n: int) -> list:
    return_list = []
    while n % 2 == 0:
        return_list.append(2)
        n //= 2
    f = 3
    while f * f <= n:
        if n % f == 0:
            return_list.append(f)
            n //= f
        else:
            f += 2
    if n != 1:
        return_list.append(n)
    return return_list

MOD用組み合わせ

def mod_cmb(n: int, k: int, p: int) -> int:
    if n < 0 or k < 0 or n < k: return 0
    if n == 0 or k == 0: return 1
    if (k > n - k):
        return mod_cmb(n, n - k, p)
    c = d = 1
    for i in range(k):
        c *= (n - i)
        d *= (k - i)
        c %= p
        d %= p
    return c * pow(d, p - 2, p) % p

Union-Find木

class UnionFind:
    # 作りたい要素数nで初期化
    # 使用するインスタンス変数の初期化
    def __init__(self, n):
        self.n = n
        # root[x]<0ならそのノードが根かつその値が木の要素数
        # rootノードでその木の要素数を記録する
        self.root = [-1]*(n+1)
        # 木をくっつける時にアンバランスにならないように調整する
        self.rank = [0]*(n+1)

    # ノードxのrootノードを見つける
    def findRoot(self, x):
        if(self.root[x] < 0): # 根
            return x
        else:
            # ここで代入しておくことで、後の繰り返しを避ける
            self.root[x] = self.findRoot(self.root[x])
            return self.root[x]
    # 木の併合、入力は併合したい各ノード
    def unite(self, x, y):
        # 入力ノードのrootノードを見つける
        x = self.findRoot(x)
        y = self.findRoot(y)
        # すでに同じ木に属していた場合
        if x == y:
            return 
        # 違う木に属していた場合rankを見てくっつける方を決める
        if self.rank[x] > self.rank[y]:
            self.root[x] += self.root[y]
            self.root[y] = x

        else:
            self.root[y] += self.root[x]
            self.root[x] = y
            # rnkが同じ（深さに差がない場合）は1増やす
            if self.rank[x] == self.rank[y]:
                self.rank[y] += 1
    # xとyが同じグループに属するか判断
    def isSameGroup(self, x, y):
        return self.findRoot(x) == self.findRoot(y)

    # ノードxが属する木のサイズを返す
    def count(self, x):
        return -self.root[self.findRoot(x)]

6. 使っているスニペット

あまりスニペットが共有されているところは見ないので、需要があるかは分かりませんが貼っておきます。
ABCではどうしても解く速度がとても重要になっている現状があるので、自身にあったスニペットは必須だと思っています。

submit.py

import sys, re
from math import ceil, floor, sqrt, pi, factorial, gcd
from copy import deepcopy
from collections import Counter, deque
from heapq import heapify, heappop, heappush
from itertools import accumulate, product, combinations, combinations_with_replacement
from bisect import bisect, bisect_left, bisect_right
from functools import reduce
from decimal import Decimal, getcontext
# input = sys.stdin.readline 
def i_input(): return int(input())
def i_map(): return map(int, input().split())
def i_list(): return list(i_map())
def i_row(N): return [i_input() for _ in range(N)]
def i_row_list(N): return [i_list() for _ in range(N)]
def s_input(): return input()
def s_map(): return input().split()
def s_list(): return list(s_map())
def s_row(N): return [s_input for _ in range(N)]
def s_row_str(N): return [s_list() for _ in range(N)]
def s_row_list(N): return [list(s_input()) for _ in range(N)]
def lcm(a, b): return a * b // gcd(a, b)
sys.setrecursionlimit(10 ** 6)
INF = float('inf')
MOD = 10 ** 9 + 7
num_list = []
str_list = []

def main():
    n = i_input()
    a, b = i_map()
    num_list = i_list()

    print()

if __name__ == '__main__':
    main()

7. おわりに

以上、普通の人である私が緑になるまでにしたことでした！
微力ですが同じく普通の人の力になれば嬉しいです！

ここまで長い文章となりましたが、読んでいただきありがとうございました。
質問やアドバイス等ありましたらコメントしていただけると喜びます！

次は水色を目指して精進していきます！

ありがとうございました！

8. よく勉強に利用させていただいたサイト

• AtCoder Problems
• AtCoder に登録したら次にやること ～ これだけ解けば十分闘える！過去問精選 10 問 ～
• レッドコーダーが教える、競プロ・AtCoder上達のガイドライン【中級編：目指せ水色コーダー！】
• アルゴリズムロジック
• 競技プロ的なアルゴリズムのスライドのまとめ