tl;dr
- EMアルゴリズムの知ったかぶり期間も長くなってしまったのでキチンとまとめたかった.
- 実装もさることながら, 数学的な理解をちゃんとしたかった.
- 混合正規分布の最尤推定問題で実装を行なった.
EMアルゴリズムを使うモチベーション
一般に観測データから混合分布に含まれる未知パラメタを推定する問題の基本的な解法は最尤推定である.
しかし, 式が複雑な形をしている場合, 解析的な (偏微分して0とおく) 方法で解を求めるのは困難である. そのような場合, 反復過程で尤度を減少させていく手法 (教師なし学習) をとる.EMアルゴリズムは教師なし学習のひとつである.
EMアルゴリズムの振舞い
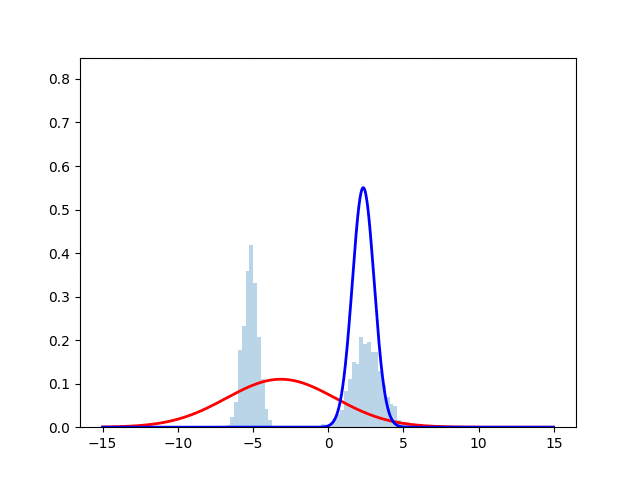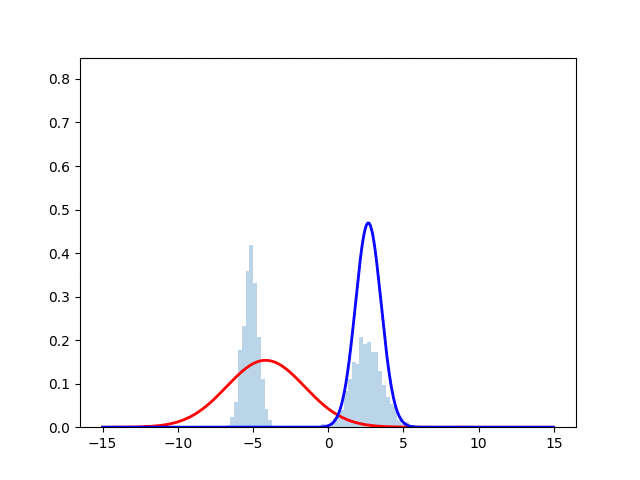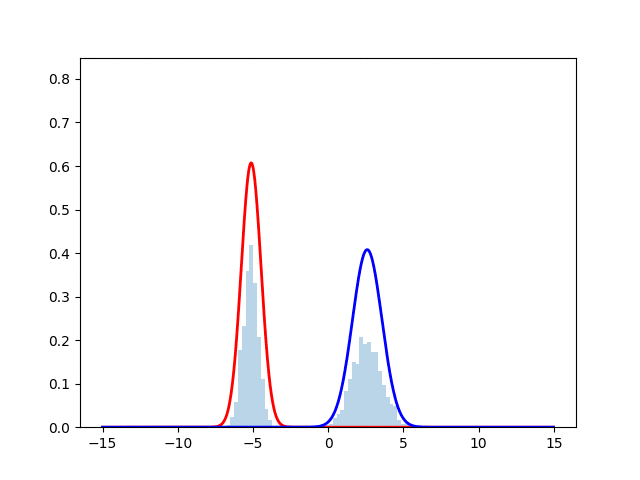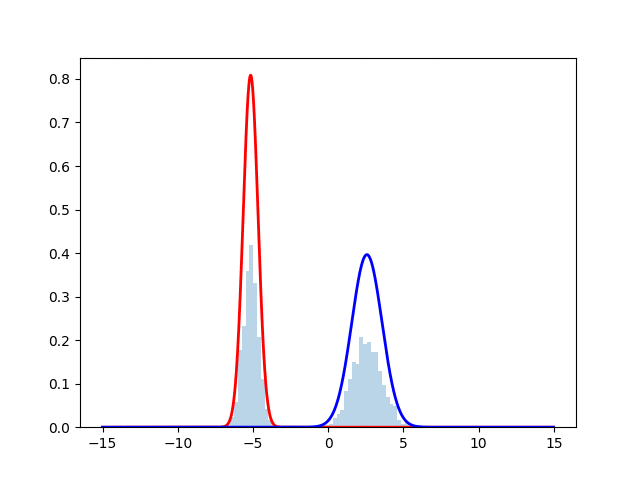
ヒストグラムが正規分布からサンプリングしたデータを表しており, 赤線と青線が最尤推定を行なった際の推定確率分布となっている. 時刻とともにサンプルにフィッティングしていく様子が見える.実際のコードは下に掲載する.
アルゴリズムアウトライン
- 未知パラメタ$\theta$の初期値$\theta^{(0)}$を与え, $K=0$とする.
- 次の関数を計算する (Eステップ)
$$ Q_K(\theta) = E_{y|x,\theta(K)} [\log p(x, y|\theta)] $$ - $Q_K(\theta)$を最大にする$\theta$を$\theta(K+1)$とする (Mステップ)
- $K←K+1$としてステップ2に戻り, これを収束するまで反復する.
クラス判別問題
仮に各データ$x_{\alpha}$がどのクラスに属するか既知であるとし,
\overline{w}_{\alpha}^{(k)} = \begin{cases}1 & \text{$x_{\alpha}が$クラス$k$に属する時} \\
0 & \text{otherwise} \end{cases} \tag{1}
の$KN$個の値 $\overline{w}_{\alpha}^{(k)}$ が指定されているとする. このときデータ${ {x_{\alpha}} }$の尤度は次のように書ける.
L = \prod_{\alpha=1}^N \frac{N_k(\alpha)}{N} p_{k(\alpha)}(x_\alpha | \theta_{k(\alpha)}) \tag{2}
ただし,
$k(\alpha)$:データ$x_{\alpha}$の属するクラス
$p_{k(\alpha)}(x_\alpha | \theta_{k(\alpha)}) $:そのクラスのデータ発生の確率密度
$\theta_{k(\alpha)}$:そのクラスの確率密度の (未知) パラメタ
とする.
尤度の対数をとると以下のようになる.
\log L = \sum_{\alpha=1}^{N}(\log N_{k(\alpha)} + \log p_{k(\alpha)}(x_{\alpha|\theta_{k}})) - N \log N \tag{3}
ここで, $x_{\alpha}$が属していないクラスでは$\overline{w}_{\alpha}^{(k)} = 0$であることを考慮すると
\log L = \sum_{\alpha=1}^{N}\overline{w}_{\alpha}^{(k)}(\log N_{k(\alpha)} + \log p_{k(\alpha)}(x_{\alpha|\theta_{k}})) - N \log N \tag{4}
と書き直せる.
ところが${\overline{w}_{\alpha}^{(k)}}$は未知である. そこで, これを欠損データとみなして, 式(4)をその期待値で置き換える. (Eステップ)
Q(\{N_k\}, \{\theta_k\}) = E[\log L] = \sum_{\alpha=1}^{N} \sum_{k=1}^K E[\overline{w}_{\alpha}^{(k)}](\log N_{k(\alpha)} + \log p_{k(\alpha)}(x_{\alpha|\theta_{k}})) - N \log N \tag{5}
いま, 確率変数が二項分布$B(n,p)$に従う時, 期待値$E(X)$が
E(X) = np
で表されることから, 0,1をとる離散変数の期待値は, それが1となる確率に等しい. ($n=1$の場合に相当)
したがって, $E[\overline{w}_{\alpha}^{(k)}]$はデータ$x_{\alpha}$がクラス$k$に属する確率に等しい.
E[\overline{w}_{\alpha}^{(k)}] = w_{\alpha}^{(k)} \tag{6}
そして, この確率は仮定した値を用いて計算した事後確率を用いることにする.
ベイズの定理より, この事後確率は次のように与えられる.
w_{\alpha}^{(k)} = \frac{\pi_k p_{k}(x_{\alpha}|\theta_k)}{\sum_{l=1}^K \pi_l p_{l}(x_{\alpha} | \theta_k)}, \qquad \pi_k = \frac{N_k}{N} \tag{7}
(実装上は, この事後確率を求める計算をEステップとして処理している.)
したがって, $Q({N_k}, {\theta_k})$は
Q(\{N_k\}, \{\theta_k\}) = \sum_{\alpha=1}^{N} \sum_{k=1}^K w_{\alpha}^{(k)}\left(\log N_{k(\alpha)} + \log p_{k(\alpha)}(x_{\alpha}|\theta_{k})\right) - N \log N \tag{8}
で与えられ, $Q$を未知数${N_k}, {\theta_k} (k = 1,2,...,K)$に関して最大化すればよい. (Mステップ)
▶︎ $Q({N_k}, {\theta_k})$の$N_k$での最大化$Q({N_k}, {\theta_k})$
$\theta_k$は固定して考えるので, 式(8)より $Q({N_k}, {\theta_k})$ を最大にするには, $\sum_{k=1}^K N_{k(\alpha)} = N$ という制約条件のもとで, $\sum_{\alpha=1}^{N} \sum_{k=1}^K w_{\alpha}^{(k)}\log N_{k(\alpha)}$を最大化すれば良い. すなわち以下のように定式化される.
\begin{aligned}
& {\text{maximize}} && \sum_{\alpha=1}^{N} \sum_{k=1}^K w_{\alpha}^{(k)}\log N_{k(\alpha)}
&\text{s.t.} && \sum_{k=1}^K N_{k(\alpha)} = N
\end{aligned} \tag{9}
そこで, ラグランジュの未定乗数を導入して
F = \sum_{\alpha=1}^{N} \sum_{k=1}^K w_{\alpha}^{(k)}\log N_{k(\alpha)} - \lambda \left(\sum_{k=1}^K N_{k(\alpha)} - N\right) \tag{10}
これを$N_{k(\alpha)}$で偏微分して0とおくことで
N_k = \frac{1}{\lambda} \sum_{\alpha = 1}^N w_{\alpha}^{(k)} \tag{11}
定義式(1)より $\sum_{k=1}^K \overline{w}_{\alpha}^{(k)} = 1$ であるから, その期待値も$E\left[\sum_{k=1}^K \overline{w}_{\alpha}^{(k)}\right] = \sum_{k=1}^K w_{\alpha}^{(k)}=1$
ゆえに,
\sum_{k=1}^K N_k = \frac{1}{\lambda} \sum_{\alpha = 1}^N \sum_{k=1}^K w_{\alpha}^{(k)} = \frac{N}{\lambda} \tag{12}
制約条件$\sum_{k=1}^K N_{k(\alpha)} = N$から$\lambda = 1$となる. ゆえに次式が得られる.
N_k = \sum_{\alpha = 1}^N w_{\alpha}^{(k)} \tag{13}
▶︎ $Q({N_k}, {\theta_k})$の$\theta_k$での最大化
式(8)より
\sum_{\alpha=1}^{N} \sum_{k=1}^K w_{\alpha}^{(k)}\log p_{k(\alpha)}(x_{\alpha}|\theta_{k}) = \sum_{\alpha=1}^{N} \log \sum_{k=1}^K p_{k(\alpha)}(x_{\alpha}|\theta_{k})^{w_{\alpha}^{(k)}} \tag{14}
この式の右辺は各クラス$k$ごとに異なるパラメタ$\theta_k$を含む項の和であるから, それぞれのクラスごとに
\log L = \log \prod_{{\alpha}=1}^N p_{k(\alpha)}(x_{\alpha}|\theta_{k})^{w_{\alpha}^{(k)}} \tag{15}
を最大にするパラメタ$\theta_k$を求めれば良い. これは各クラス$k$ごとにデータ$x_1, x_2, …, x_N$がそれぞれ$w_1^{(k)}, w_2^{(k)}, … ,w_N^{(k)} $個あるときのパラメタ$\theta_k$の最尤推定と等価となる.
▶︎ 正規分布のパラメタ$\mu, \sigma$の最尤推定値
今回は, 混合正規分布を扱うことから, $p_{k(\alpha)}(x_\alpha | \theta_{k(\alpha)}) = \mathcal{N}(x_{\alpha}|\mu_k, \Sigma_k) = \frac{\exp(- w_{\alpha}^{(k)}(x_{\alpha} - \mu_k)/2 \Sigma_k)}{\sqrt{2 \pi \Sigma_k}}$とする.
式(15)より, 負の対数尤度が以下のように書ける.
\begin{eqnarray*}
J&=&- \log L\\
&=& - \log \prod_{\alpha = 1}^N \left(\frac{\exp(- (x_{\alpha} - \mu_k)/2 \Sigma_k)}{\sqrt{2 \pi \Sigma_k}}\right)^{w_{\alpha}}\\
&=& - \log \prod_{\alpha = 1}^N \frac{\exp(- w_{\alpha}^{(k)}(x_{\alpha} - \mu_k)/2 \Sigma_k)}{\left(\sqrt{2 \pi \Sigma_k}\right)^{w_{\alpha}}}\\
&=& - \log \frac{\exp \left(- \sum_{\alpha=1}^N (w_{\alpha}^{(k)}(x_{\alpha} - \mu_k)/2 \Sigma_k)\right)}{\left(\sqrt{2 \pi \Sigma_k}\right)^{N w_{\alpha}}}\\
&=& \frac{1}{2 \Sigma} \sum_{\alpha=1}^N w_{\alpha}^{(k)}(x_{\alpha} - \mu_k)^2 + \frac{N w_{\alpha}^{(k)}}{2} \log 2\pi \Sigma \\ \tag{16}
\end{eqnarray*}
この負の対数尤度$J$を最小にする$\mu_k$と$\Sigma_k$が正規分布のパラメタ最尤推定値となる.
すなわち, $J$を$\mu_k$, $\Sigma_k$で偏微分して$0$と置けばよい.
\begin{eqnarray*}
\frac{\partial J}{\partial \mu_k} & = & 0 \\
\iff&& - \frac{1}{\Sigma} \sum_{\alpha=1}^{N} w_{\alpha}^{(k)} (x_{\alpha} - \mu_k) = 0 \\
\iff&& \sum_{\alpha=1}^N w_{\alpha} x_{\alpha} - \mu_k \sum_{\alpha=1}^N w_{\alpha} = 0 \\
\iff&& \mu_k = \frac{\sum_{\alpha=1}^N w_{\alpha} x_{\alpha}}{\sum_{\alpha=1}^N w_{\alpha}} \\
\iff&& \mu_k = \frac{1}{N_k} \sum_{\alpha=1}^N w_{\alpha} x_{\alpha} &&\left(\because \sum_{\alpha=1}^N w_{\alpha} = N_k\right )\\ \tag{17}
\end{eqnarray*}
\begin{eqnarray*}
\frac{\partial J}{\partial \Sigma_k} & = & 0 \\
\iff&& - \frac{1}{2\Sigma^2} \sum_{\alpha=1}^{N} w_{\alpha}^{(k)} (x_{\alpha} - \mu_k)^2 + \frac{N w_{\alpha}}{2} \cdot \frac{1}{2 \pi \Sigma_k} \cdot 2 \pi = 0 \\
\iff&& - \frac{1}{\Sigma_k}\sum_{\alpha=1}^N w_{\alpha} (x_{\alpha} - \mu_k)^2 + N w_{\alpha} = 0 \\
\iff&& \sum_{\alpha=1}^N w_{\alpha} \left( 1 - \frac{(x_{\alpha} - \mu_k)^2}{\Sigma_k} \right) = 0 \\
\iff&& \sum_{\alpha=1}^N w_{\alpha} =\sum_{\alpha=1}^N w_{\alpha} (x_{\alpha} - \mu_k)^2 \cdot \frac{1}{\Sigma_k} \\
\iff&&\Sigma_k = \frac{1}{N_k}\sum_{\alpha=1}^N w_{\alpha} (x_{\alpha} - \mu_k)^2 &&\left(\because \sum_{\alpha=1}^N w_{\alpha} = N_k\right )\\ \tag{18}
\end{eqnarray*}
以上より, モデルパラメタの推定値を整理すると以下のようになる. (コードで実装する式はこの部分になる.)
\begin{eqnarray*}
w_{\alpha}^{(k)} &=& \frac{\pi_k p_{k}(x_{\alpha}|\theta_k)}{\sum_{l=1}^K \pi_l p_{l}(x_{\alpha} | \theta_k)}\tag{19} \\
\pi_k &=& \frac{N_k}{N} \tag{20} \\
N_k &=& \sum_{\alpha = 1}^N w_{\alpha}^{(k)}\tag{21} \\
\hat{\mu} &=& \frac{1}{N_k}\sum_{\alpha = 1}^N w_{\alpha}^{(k)}x_{\alpha}\tag{22} \\
\hat{\sigma}^2 &=& \frac{1}{N_k}\sum_{\alpha=1}^N w_{\alpha}^{(k)}(x_{\alpha} - \mu_{\alpha})^2\tag{23} \\
\end{eqnarray*}
実装
実装は, こちらの記事を参考にさせていただきました. 事後確率の算出コードだけ少し改変してあります.
以下のコードを実行すればgifアニメーションまで出ます.
import numpy as np
from matplotlib import pyplot
import matplotlib.animation as animation
import sys
def create_data(N, K):
X, mu_list, sigma_list = [], [], []
for i in range(K):
loc = (np.random.rand() - 0.7) * 10.0 # 平均
scale = np.random.rand() * 2.0 # 標準偏差
X = np.append(X, np.random.normal(
loc = loc,
scale = scale,
size = int(N / K) #出力配列のサイズ
))
mu_list = np.append(mu_list, loc)
sigma_list = np.append(sigma_list, scale)
return (X, mu_list, sigma_list)
def gaussian(mu, sigma):
def f(x):
return np.exp(-0.5 * (x - mu) ** 2 / sigma) / np.sqrt(2 * np.pi * sigma)
return f
# Eステップにおいて事後確率を計算する
def estimate_posterior_probability(X, pi, gf):
l = np.zeros((X.size, pi.size))
for (i, x) in enumerate(X):
l[i, :] = gf(x)
numerator = pi * l
denominator = np.vectorize(lambda y: y)((l*pi).sum(axis=1).reshape(-1, 1))
return numerator / denominator
# MステップにおいてQ関数を最大化するパラメタ mu, sigma, pi を計算する
def maximize_parameters(X, post_pro):
N = post_pro.sum(axis=0)
mu = (post_pro * X.reshape((-1, 1))).sum(axis=0) / N
sigma = (post_pro * (X.reshape(-1, 1) - mu) ** 2).sum(axis=0) / N
pi = N / X.size
return (mu, sigma, pi)
# Q関数を計算する
def calc_Q(X, mu, sigma, pi, post_pro):
Q = (post_pro * (np.log(pi * (2 * np.pi * sigma) ** (-0.5)))).sum()
for (i, x) in enumerate(X):
Q += (post_pro[i, :] * (-0.5 * (x - mu) ** 2 / sigma)).sum()
return Q
if __name__ == '__main__':
# data
K = 2
N = 1500 * K
X, mu_list, sigma_list = create_data(N, K)
colors = ['r', 'b', 'g']
# 収束条件
epsilon = 1e-20
# 未知パラメタを初期化する
pi = np.random.rand(K)
mu = np.random.randn(K)
sigma = np.abs(np.random.randn(K))
Q = -sys.float_info.max
delta = None
ims = []
fig = pyplot.figure()
n, bins, _ = pyplot.hist(X, 50, normed=1, alpha=0.3)
seq = np.arange(-15, 15, 0.02)
# EMアルゴリズム
while delta == None or delta >= epsilon:
gf = gaussian(mu, sigma)
# Eステップ:
post_pro = estimate_posterior_probability(X, pi, gf)
# Mステップ: Q関数を最大化するパラメタ mu, sigma, pi を求める
mu, sigma, pi = maximize_parameters(X, post_pro)
# plot data
tmp = []
for i in range(K):
im = pyplot.plot(seq, gaussian(mu[i], sigma[i])(seq), linewidth=2.0, color=colors[i])
tmp.append(im[0])
ims.append(tmp)
# Q関数の計算
Q_new = calc_Q(X, mu, sigma, pi, post_pro)
delta = Q_new - Q
Q = Q_new
# plot
ani = animation.ArtistAnimation(fig, ims, interval=300)
ani.save('test1.gif', writer="imagemagick")
pyplot.show()
以上です.
統計的機械学習のクラシックな手法は数学があざやかなものが多くて楽しいですね!
参考
- これなら分かる最適化数学―基礎原理から計算手法まで / 金谷 健一
- pythonで混合正規分布実装 (https://qiita.com/ta-ka/items/3e8b127620ac92a32864)