はじめに

pythonで混合正規分布を実装しました．
教科書として『はじめてのパターン認識』を使いました．

本記事の構成

はじめに
混合正規分布
- 混合正規分布モデル
- 隠れ変数と事後確率
- 対数尤度とQ関数
EMアルゴリズムによるパラメータ推定
pythonでの実装
結果
おわりに

混合正規分布

データ分布に確率モデルを当てはめると，各データがどのクラスタに属するかを確率的に決めることができます．
多くの確率モデルは単峰性の確率分布しか表現できないため，全体の確率分布を複数の確率モデルの重み付け線形和でモデル化する必要があります．
クラスタ数を $K$，$k$ 番目のクラスタの確率モデルを $p_k(\boldsymbol x)$ とし，全体の確率分布を以下のように表します．

p(\boldsymbol x) = \sum_{k = 1}^K \pi_kp_k(\boldsymbol x)

$\pi_k$ は $k$ 番目の確率モデルの重みとなります．
確率モデルとして正規分布を用いたものを 混合正規分布モデル と呼びます．

混合正規分布モデル

$k$ 番目のクラスタを表す $d$ 次元正規分布関数を以下のように表します．

N(\boldsymbol x \ | \ \boldsymbol \mu_k, \boldsymbol \Sigma_k) = \frac{1}{(2\pi)^{1/d} \ |\boldsymbol \Sigma_k|^{1/2}}\exp\bigl(-\frac{1}{2}(\boldsymbol x - \boldsymbol \mu_k)^T \boldsymbol \Sigma_k^{-1}(\boldsymbol x - \boldsymbol \mu_k)\bigr)

全体の分布は，これらの線形和として表されます．

p(\boldsymbol x) = \sum_k^K \pi_k N(\boldsymbol x \ | \ \boldsymbol \mu_k, \boldsymbol \Sigma_k), \ 0 \leq \pi_k \leq 1, \ \sum_{k = 1}^K \pi_k = 1

$\pi_k$ を混合比と呼び，混合正規分布モデルのパラメータは以下になります．

\boldsymbol \pi = (\pi_1, ..., \pi_K), \ \boldsymbol \mu = (\boldsymbol \mu_1, ..., \boldsymbol \mu_K), \ \boldsymbol \Sigma = (\boldsymbol \Sigma_1, ..., \boldsymbol \Sigma_K)

全体のデータをうまく表現できるような $\boldsymbol \pi, \ \boldsymbol \mu, \ \boldsymbol \Sigma$ が必要となります．
しかし，各データがどのクラスタに属するかは不明であるため，各パラメータを直接求めることはできません．

隠れ変数と事後確率

混合正規分布モデルでは，全体のデータから $\boldsymbol \pi, \ \boldsymbol \mu, \ \boldsymbol \Sigma$ を推定するために，
各データ $\boldsymbol x$ がどのクラスタに属するかを表す $K$ 次元の隠れ変数 $\boldsymbol z = (z_1, ..., z_K)^T$ を導入します．
$z_k$ は，データが $k$ 番目のクラスタに属していれば $1$，属していなければ $0$ をとります．

\sum_{k = 1}^K z_k = 1, \ \boldsymbol z = (0, ..., 0, 1, 0, ..., 0)^T

観測される $\boldsymbol x$ と隠れ変数 $\boldsymbol z$ の同時分布 $p(\boldsymbol x, \boldsymbol z)$ は以下になります．

p(\boldsymbol x, \boldsymbol z) = p(\boldsymbol z)p(\boldsymbol x \ | \ \boldsymbol z)

また，隠れ変数の分布 $p(\boldsymbol z)$ および観測データの隠れ変数による条件付き分布 $p(\boldsymbol x \ | \ \boldsymbol z)$ は以下のように表せます．

\begin{align}
& p(\boldsymbol z) = \prod_{k = 1}^K \pi_k^{z_k} \\
& p(\boldsymbol x \ | \ \boldsymbol z) = \prod_{k = 1}^K \big[N(\boldsymbol x \ | \ \boldsymbol \mu_k, \boldsymbol \Sigma_k)\bigr]^{z_k}
\end{align}

さらに，同時分布 $p(\boldsymbol x, \boldsymbol z)$ をすべての $\boldsymbol z$ について加えることで，$p(\boldsymbol x)$ を求めることができます．

\begin{align}
p(\boldsymbol x) &= \sum_{\substack{k = 1 \\ (z_k = 1, z_{j \neq k} = 0)}}^K p(\boldsymbol x, \boldsymbol z) \\
&= \sum_{\substack{k = 1 \\ (z_k = 1, z_{j \neq k} = 0)}}^K p(\boldsymbol z)p(\boldsymbol x \ | \ \boldsymbol z) \\
&= \sum_{\substack{k = 1 \\ (z_k = 1, z_{j \neq k} = 0)}}^K \prod_{k = 1}^K \pi_k^{z_k} \prod_{k = 1}^K \big[N(\boldsymbol x \ | \ \boldsymbol \mu_k, \boldsymbol \Sigma_k)\bigr]^{z_k} \\
&= \sum_{k = 1}^K \pi_kN(\boldsymbol x \ | \ \boldsymbol \mu_k, \boldsymbol \Sigma_k)
\end{align}

以上の分布を用いると，隠れ変数の事後確率 $\gamma(z_k)$ は以下のように表されます．

\begin{align}
\gamma(z_k) &\equiv p(z_k = 1 \ | \ \boldsymbol x) \\
&\\
&= \frac{p(z_k = 1)p(\boldsymbol x \ | \ z_k = 1)}{\sum_{j = 1}^K p(z_j = 1)p(\boldsymbol x \ | \ z_j = 1)} \\
&\\
&= \frac{\pi_kN(\boldsymbol x \ | \ \boldsymbol \mu_k, \boldsymbol \Sigma_k)}{\sum_{j = 1}^K \pi_jN(\boldsymbol x \ | \ \boldsymbol \mu_j, \boldsymbol \Sigma_j)} \tag{*}
\end{align}

対数尤度とQ関数

観測データ $\boldsymbol X$ および隠れ変数 $\boldsymbol Z$ を以下のように表します．
$C_k$ は，クラスタ $k$ を表します．

\begin{align}
& \boldsymbol X = (\boldsymbol x_1, ..., \boldsymbol x_N), \ \boldsymbol x_i = (x_{i1}, ..., x_{id})^T \\
& \boldsymbol Z = (\boldsymbol z_1, ..., \boldsymbol z_N), \ \boldsymbol z_i = (z_{i1}, ..., z_{iK})^T \\
& z_{ik} = \begin{cases}
1 \ (x_i \in C_k) \\
0 \ (x_i \notin C_k)
\end{cases}
\end{align}

観測データと隠れ変数を合わせた集合を完全データと呼びます．

\boldsymbol Y = (\boldsymbol x_1, ..., \boldsymbol x_N, \boldsymbol z_1, ..., \boldsymbol z_N) = (\boldsymbol X, \boldsymbol Z)

混合正規分布のパラメータ $\boldsymbol \pi, \ \boldsymbol \mu, \ \boldsymbol \Sigma$ は，完全データの尤度を最大にするパラメータで求めることとします．
完全データの尤度は以下のように表せます．

\begin{align}
p(\boldsymbol Y \ | \ \boldsymbol \pi, \ \boldsymbol \mu, \ \boldsymbol \Sigma) &= p(\boldsymbol Z \ | \ \boldsymbol \pi, \ \boldsymbol \mu, \ \boldsymbol \Sigma) p(\boldsymbol X \ | \ \boldsymbol Z, \ \boldsymbol \pi, \ \boldsymbol \mu, \ \boldsymbol \Sigma) \\
&\\
&= \prod_{i = 1}^N \prod_{k = 1}^K \bigl[\pi_kN(\boldsymbol x_i \ | \ \boldsymbol \mu_k, \boldsymbol \Sigma_k) \bigr]^{z_{ik}}
\end{align}

最尤推定値を求めるために対数尤度に変形します．

\begin{align}
\tilde{L} &= \ln p(\boldsymbol Y \ | \ \boldsymbol \pi, \ \boldsymbol \mu, \ \boldsymbol \Sigma) \\
&\\
&= \sum_{i = 1}^N \sum_{k = 1}^K z_{ik} \ln \pi_k + \sum_{i = 1}^N \sum_{k = 1}^K z_{ik} \ln N(\boldsymbol x_i \ | \ \boldsymbol \mu_k, \boldsymbol \Sigma_k) \\
&\\
&= \sum_{i = 1}^N \sum_{k = 1}^K z_{ik} \ln \pi_k + \sum_{i = 1}^N \sum_{k = 1}^K z_{ik} \bigl(-\frac{d}{2}\ln (2\pi) + \frac{1}{2} \ln \bigl|\boldsymbol \Sigma_k \bigr|^{-1} - \frac{1}{2}(\boldsymbol x_i - \boldsymbol \mu_k)^T \boldsymbol \Sigma_k^{-1}(\boldsymbol x_i - \boldsymbol \mu_k) \bigr)
\end{align}

対数尤度の隠れ変数に関する期待値をとります．

\begin{align}
L &= E_z \bigl\{\tilde{L} \bigr\} \\
&\\
&= \sum_{i = 1}^N \sum_{k = 1}^K E_{z_{ik}} \bigl\{z_{ik} \bigr\} \ln \pi_k + \sum_{i = 1}^N \sum_{k = 1}^K E_{z_{ik}} \bigl\{z_{ik} \bigr\} \bigl(-\frac{d}{2}\ln (2\pi) + \frac{1}{2} \ln \bigl|\boldsymbol \Sigma_k \bigr|^{-1} - \frac{1}{2}(\boldsymbol x_i - \boldsymbol \mu_k)^T \boldsymbol \Sigma_k^{-1}(\boldsymbol x_i - \boldsymbol \mu_k) \bigr)
\end{align}

隠れ変数に関する期待値は，式(*)より以下のようになり，隠れ変数の事後確率となります．

\begin{align}
E_{z_{ik}} \bigl\{z_{ik} \bigr\} &= \sum_{z_{ik} = \{0, 1\}} z_{ik}p(z_{ik} \ | \ \boldsymbol x_i, \pi_k, \boldsymbol \mu_k, \boldsymbol \Sigma_k) \\
&\\
&= 1 \times p(z_{ik} = 1 \ | \ \boldsymbol x_i) \\
&\\
& = \frac{p(z_{ik} = 1)p(\boldsymbol x_i \ | \ z_{ik} = 1)}{\sum_{j = 1}^K p(z_{ij} = 1)p(\boldsymbol x \ | \ z_{ij} = 1)} \\
&\\
&= \frac{\pi_kN(\boldsymbol x \ | \ \boldsymbol \mu_k, \boldsymbol \Sigma_k)}{\sum_{j = 1}^K \pi_jN(\boldsymbol x \ | \ \boldsymbol \mu_j, \boldsymbol \Sigma_j)} \\
&\\
&= \gamma(z_{ik})
\end{align}

$L$ の隠れ変数の期待値を事後確率で置換した関数を Q関数 と呼びます．

Q = \sum_{i = 1}^N \sum_{k = 1}^K \gamma(z_{ik}) \ln \pi_k + \sum_{i = 1}^N \sum_{k = 1}^K \gamma(z_{ik}) \ln \pi_k \bigl(-\frac{d}{2}\ln (2\pi) + \frac{1}{2} \ln \bigl|\boldsymbol \Sigma_k \bigr|^{-1} - \frac{1}{2}(\boldsymbol x_i - \boldsymbol \mu_k)^T \boldsymbol \Sigma_k^{-1}(\boldsymbol x_i - \boldsymbol \mu_k) \bigr)

EMアルゴリズムによるパラメータ推定

隠れ変数がある確率モデルのパラメータの最尤推定値を求める手法として EMアルゴリズム を用います．
EMアルゴリズムは2つのステップで構成されます．

Expectationステップ：隠れ変数に関する期待値を取る操作．モデルパラメータを固定して隠れ変数の事後確率を求める．
Maximizationステップ：Eステップで求めた隠れ変数の事後確率を用いてQ関数を最大にするモデルパラメータを求める．

EMアルゴリズムは完全データの対数尤度に変化がなくなるまで，EステップおよびMステップを繰り返します．
収束値は初期値に依存するため，局所最適解しか得られません．
初期値を変えて複数回EMアルゴリズムを使って最尤推定値を求め，その中から良いものを選択する必要があります．
EMアルゴリズムをまとめると，次のようになります．

$\pi_k, \ \boldsymbol \mu_k, \ \boldsymbol \Sigma_k$ の初期化
Eステップ：現在のパラメータ $\pi_k, \ \boldsymbol \mu_k, \ \boldsymbol \Sigma_k$ を用いた事後確率 $\gamma(z_{ik})$ の推定
$$\gamma(z_{ik}) = \frac{\pi_kN(\boldsymbol x \ | \ \boldsymbol \mu_k, \boldsymbol \Sigma_k)}{\sum_{j = 1}^K \pi_jN(\boldsymbol x \ | \ \boldsymbol \mu_j, \boldsymbol \Sigma_j)}$$
Mステップ：推定した $\gamma(z_{ik})$ を用いたモデルパラメータの再推定
$$
\begin{align}
& N_k = \sum_{i = 1}^N \gamma(z_{ik}) \
& \
& \boldsymbol \mu_k = \frac{1}{N_k} \sum_{i = 1}^N \gamma(z_{ik}) \boldsymbol x_i \
& \
& \boldsymbol \Sigma_k = \frac{1}{N_k} \sum_{i = 1}^N \gamma(z_{ik}) (\boldsymbol x_i - \boldsymbol \mu_k)(\boldsymbol x_i - \boldsymbol \mu_k)^T \
& \
& \pi_k = \frac{N_k}{N}
\end{align}
$$
終了判定：完全データの対数尤度が収束していない場合2.から再計算．収束していれば終了．

pythonでの実装

以下のように実装しました．

mixturesofgaussian.py

import numpy
from matplotlib import pyplot
import sys

def create_data(N, K):
    X, mu_star, sigma_star = [], [], []
    for i in range(K):
        loc = (numpy.random.rand() - 0.5) * 10.0 # range: -5.0 - 5.0
        scale = numpy.random.rand() * 3.0 # range: 0.0 - 3.0
        X = numpy.append(X, numpy.random.normal(loc = loc, scale = scale, size = int(N / K)))
        mu_star = numpy.append(mu_star, loc)
        sigma_star = numpy.append(sigma_star, scale)
    return (X, mu_star, sigma_star)

def gaussian(mu, sigma):
    def f(x):
        return numpy.exp(-0.5 * (x - mu) ** 2 / sigma) / numpy.sqrt(2 * numpy.pi * sigma)
    return f

def estimate_posterior_likelihood(X, pi, gf):
    l = numpy.zeros((X.size, pi.size))
    for (i, x) in enumerate(X):
        l[i, :] = gf(x)
    return pi * l * numpy.vectorize(lambda y: 1 / y)(l.sum(axis = 1).reshape(-1, 1))

def estimate_gmm_parameter(X, gamma):
    N = gamma.sum(axis = 0)
    mu = (gamma * X.reshape((-1, 1))).sum(axis = 0) / N
    sigma = (gamma * (X.reshape(-1, 1) - mu) ** 2).sum(axis = 0) / N
    pi = N / X.size
    return (mu, sigma, pi)

def calc_Q(X, mu, sigma, pi, gamma):
    Q = (gamma * (numpy.log(pi * (2 * numpy.pi * sigma) ** (-0.5)))).sum()
    for (i, x) in enumerate(X):
        Q += (gamma[i, :] * (-0.5 * (x - mu) ** 2 / sigma)).sum()
    return Q

if __name__ == '__main__':

    # data
    K = 2
    N = 1000 * K
    X, mu_star, sigma_star = create_data(N, K)

    # termination condition
    epsilon = 0.000001

    # initialize gmm parameter
    pi = numpy.random.rand(K)
    mu = numpy.random.randn(K)
    sigma = numpy.abs(numpy.random.randn(K))
    Q = -sys.float_info.max
    delta = None

    # EM algorithm
    while delta == None or delta >= epsilon:
        gf = gaussian(mu, sigma)

        # E step: estimate posterior probability of hidden variable gamma
        gamma = estimate_posterior_likelihood(X, pi, gf)

        # M step: miximize Q function by estimating mu, sigma and pi
        mu, sigma, pi = estimate_gmm_parameter(X, gamma)

        # calculate Q function
        Q_new = calc_Q(X, mu, sigma, pi, gamma)
        delta = Q_new - Q
        Q = Q_new

    # result
    print(u'mu*: %s, simga*: %s' % (str(numpy.sort(numpy.around(mu_star, 3))), str(numpy.sort(numpy.around(sigma_star, 3)))))
    print(u'mu : %s, sgima : %s' % (str(numpy.sort(numpy.around(mu, 3))), str(numpy.sort(numpy.around(sigma, 3)))))

    # plot
    n, bins, _ = pyplot.hist(X, 50, density = True, alpha = 0.3)
    seq = numpy.arange(-15, 15, 0.02)
    for i in range(K):
        pyplot.plot(seq, gaussian(mu[i], sigma[i])(seq), linewidth = 2.0)
    pyplot.savefig('gmm_graph.png')
    pyplot.show()

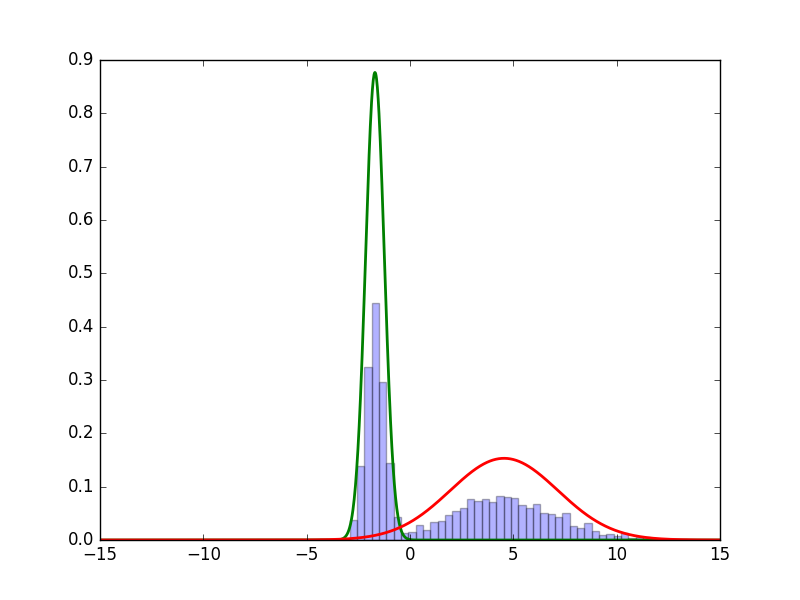
結果

以下のような結果が得られました．
妥当な推定ができていそうです．

おわりに

pythonで混合正規分布を実装することができました．
Mステップにおける各パラメータの導出方法やEMアルゴリズムの性質など理解できていない部分があるので，
今後勉強して追記します．

pythonで混合正規分布実装