はじめに
Q学習以外のTD学習であるSarsa、Actor-Critic法を紹介していく。Q学習についてはこの記事、倒立振子問題についてはこの記事で紹介した。
理論
Sarsa(State-Action-Reward-State-Action)
SarsaはQ学習でQ値を更新する部分を少し変更した(実装の面では似た)理論である。具体的には以下の通りである。
Q学習
$$Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha(r_{t+1}+\gamma \max_{a_{t+1}}Q(s_{t+1},a_{t+1})-Q(s_t,a_t))$$
Sarsa$$Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha(r_{t+1}+\gamma Q(s_{t+1},a_{t+1})-Q(s_t,a_t))$$
この二つは将来に関する項が異なっている。Q学習では状態$s_{t+1}$における最大の価値を採用しているが、Sarsaでは実際に次の行動$a_{t+1}$を決め、価値$Q(s_{t+1}$,$a_{t+1})$を採用している。Q学習では次の行動をQ値の更新後に決定し、Sarsaでは次の行動をQ値の更新前に決定する。Q学習は価値が最大となるような行動で状態更新する(Valueベース)ことから方策オフ型のアルゴリズム、Sarsaは戦略に基づいた行動で状態更新する(Policy)ことから方策オン型のアルゴリズムと呼ばれている。この二つに良し悪しはなく、考えるモデルによって変わる。
Actor Critic法
Actor Critic法はValueベースとPolicyベースを組み合わせた手法である。Sarsaでは行動決定と状態更新は同一のQテーブルで行われていたが、Actor Critic法では行動決定Actorと状態更新Criticを異なるテーブルで行い、これらを相互に更新し学習する。Q値の更新は以下のように行う。
$$Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha(r_{t+1}+\gamma V(s_{t+1})-Q(s_t,a_t))$$
#実装
倒立振子問題(CartPole)を例にそれぞれの方法で学習させる。この問題に関する細かな条件はここを参照した(「はじめに」ある記事にも書いた)。Q学習のコードはいくつかのファイルに分けて書いたが、解説には不便であったので一つにまとめて書く。小分けに紹介し、コード全体はGitHubを参照していただきたい。
Sarsa
まず、ライブラリーの呼び出し、定数、パラメータの設定、観測値の離散化などを行う。
import os, sys
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation
import gym
# 定数
MAX_STEPS = 200 # 最大のステップ数
NUM_EPISODES = 2000 # 最大の試行回数
NUM_DIZITIZED = 6 # 各状態の分割数
# 学習パラメータ
GAMMA = 0.99 # 時間割引率
ETA = 0.5 # 学習係数
# 離散化
def bins(clip_min, clip_max, num):
# 観測した状態デジタル変換する閾値を求める
return np.linspace(clip_min, clip_max, num + 1)[1:-1]
def analog2digitize(observation):
#状態の離散化
cart_pos, cart_v, pole_angle, pole_v = observation
digitized = [
np.digitize(cart_pos, bins=bins(-2.4, 2.4, NUM_DIZITIZED)),
np.digitize(cart_v, bins=bins(-3.0, 3.0, NUM_DIZITIZED)),
np.digitize(pole_angle, bins=bins(-0.5, 0.5, NUM_DIZITIZED)),
np.digitize(pole_v, bins=bins(-2.0, 2.0, NUM_DIZITIZED))
]
return sum([x * (NUM_DIZITIZED**i) for i, x in enumerate(digitized)])
これで学習方法(パラメータを除く)などに依存しない部分の設定ができたので次に進む。
Qテーブルの更新や行動決定に関するクラスを作成する。
class Sarsa:
def __init__(self, num_states, num_actions):
self.num_actions = num_actions
self.q_table = np.random.uniform(low=-1, high=1, size=(NUM_DIZITIZED**num_states, num_actions))
# Qテーブル更新
def update_Qtable(self, observation, action, reward, observation_next, action_next):
state = analog2digitize(observation)
state_next = analog2digitize(observation_next)
td = reward + GAMMA * self.q_table[state_next, action_next] - self.q_table[state, action]
self.q_table[state, action] += ETA * td
def decide_action(self, observation, episode):
state = analog2digitize(observation)
# ε-greedy法で行動を選択する
epsilon = 0.5 * (1 / (episode + 1))
if epsilon <= np.random.rand():
# 最も価値の高い行動を行う。
action = np.argmax(self.q_table[state][:])
else:
# 適当に行動する。
action = np.random.choice(self.num_actions)
return action
Q学習と本質的に異なる部分はQテーブル更新の将来に関する項のみである。最後に学習の実行、報酬の設定、エピソードごとの報酬などの描画、最後のエピソードの描画を行う。
class Env():
def __init__(self, env, sarsa_class):
self.env = env
self.sarsa_class = sarsa_class
def run(self):
# 状態数を取得
num_states = self.env.observation_space.shape[0]
# 行動数を取得
num_actions = self.env.action_space.n
sarsa = self.sarsa_class(num_states, num_actions)
step_list = []
mean_list = []
std_list = []
for episode in range(NUM_EPISODES):
observation = self.env.reset() # 環境の初期化
frames = []
# 初期行動を求める
action = sarsa.decide_action(observation, 0)
for step in range(MAX_STEPS):
if episode == NUM_EPISODES-1: frames.append(self.env.render(mode='rgb_array'))
# 行動a_tの実行により、s_{t+1}, r_{t+1}を求める
observation_next, _, done, _ = self.env.step(action)
# 初期行動を求める
action_next = sarsa.decide_action(observation_next, episode+1)
# 報酬を与える
if done: # ステップ数が200経過するか、一定角度以上傾くとdoneはtrueになる
if step < 195:
reward = -1 # 失敗したので-1の報酬を与える
else:
reward = 1 # 成功したので+1の報酬を与える
else:
reward = 0
# Qテーブル, Vを更新する
sarsa.update_Qtable(observation, action, reward, observation_next, action_next)
# 観測値を更新する
observation = observation_next
# 行動を更新する
action = action_next
# 終了時の処理
if done:
step_list.append(step+1)
print('{}回目の試行は{}秒持ちました。(max:200秒)'.format(episode, step + 1))
break
if episode == NUM_EPISODES-1:
plt.figure()
patch = plt.imshow(frames[0])
plt.axis('off')
def animate(i):
patch.set_data(frames[i])
anim = animation.FuncAnimation(plt.gcf(), animate, frames=len(frames), interval=50)
anim.save('movie_cartpole_v0_{}.gif'.format(episode+1), "ffmpeg")
es = np.arange(0, len(step_list))
plt.clf()
plt.plot(es, step_list)
plt.savefig("reward.png")
for i, s in enumerate(step_list):
if i < 100:
mean_list.append(np.average(step_list[:i+1]))
std_list.append(np.std(step_list[:i+1]))
else:
mean_list.append(np.average(step_list[i-100:i+1]))
std_list.append(np.std(step_list[i-100:i+1]))
mean_list = np.array(mean_list)
std_list = np.array(std_list)
plt.clf()
plt.plot(es, mean_list)
plt.fill_between(es, mean_list-std_list, mean_list+std_list, alpha=0.2)
plt.savefig("mean_var.png")
if __name__ == "__main__":
env = gym.make("CartPole-v0")
env = Env(env, Sarsa)
env.run()
行動を決めるところに気をつける。
これによって得られた最後のエピソードは以下のようになった。
エピソードごとの報酬の遷移は以下のようになった。
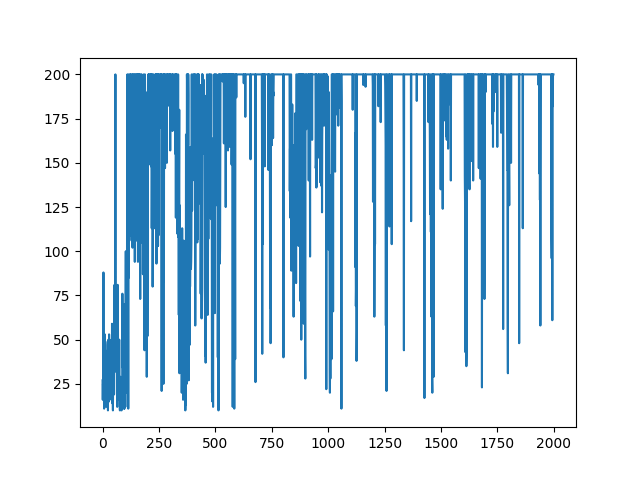
直近100エピソードの報酬の平均およびそのばらつき(標準偏差)は以下のようになった。
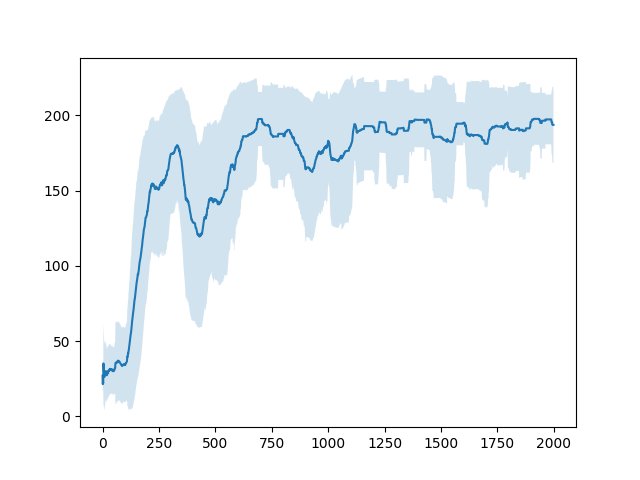
この結果はQ学習や後に見せるActor-Critic法で行った結果と比べて悪い。これはSarsaが他の手法に比べて戦略的に失敗するような行動を起こすことが多いからだと考えられます(これは私の考察なのでそもそもコードにmsがあったなどさまざまな原因が考えられます。その可能性を防ぐため、いくつか他の人が書いたコードと比較しましたが学習法の誤りは発見できませんでした。)。
Actor-Critic法
Actor-Critic法で学習させたコードを紹介する。Sarsaのコードを改変して作ったので同じ部分は省略する。
この手法では以下のように行動を選択するQテーブルと状態を評価するVを定義する。
# 行動選択
class Actor:
def __init__(self, num_states, num_actions):
self.num_actions = num_actions
self.q_table = np.random.uniform(low=-1, high=1, size=(NUM_DIZITIZED**num_states, num_actions))
def decide_action(self, observation, episode):
state = analog2digitize(observation)
# ε-greedy法で行動を選択する
epsilon = 0.5 * (1 / (episode + 1))
if epsilon <= np.random.rand():
# 最も価値の高い行動を行う。
action = np.argmax(self.q_table[state][:])
else:
# 適当に行動する。
action = np.random.choice(self.num_actions)
return action
# 状態評価
class Critic:
def __init__(self, num_states):
self.V = np.zeros(NUM_DIZITIZED**num_states)
Sarsaとは異なり、Qテーブル、Vのどちらも更新しなければいけないので、Qテーブルを定義したクラスには更新に関する関数は書かなかった。この関数は次の部分に加えた。
# Actor Critic 学習
class ActorCritic():
def __init__(self, env, actor_class, critic_class):
self.env = env
self.actor_class = actor_class
self.critic_class = critic_class
def run(self):
# 状態数を取得
num_states = self.env.observation_space.shape[0]
# 行動数を取得
num_actions = self.env.action_space.n
actor = self.actor_class(num_states, num_actions)
critic = self.critic_class(num_states)
# Qテーブル, Vの更新
def update_Qtable_V(observation, action, reward, observation_next):
state = analog2digitize(observation)
state_next = analog2digitize(observation_next)
td = reward + GAMMA * critic.V[state_next] - critic.V[state]
actor.q_table[state, action] += ETA * td
critic.V[state] += ETA * td
step_list = []
mean_list = []
std_list = []
for episode in range(NUM_EPISODES):
observation = self.env.reset() # 環境の初期化
frames = []
for step in range(MAX_STEPS):
if episode == NUM_EPISODES-1: frames.append(self.env.render(mode='rgb_array'))
# 行動を求める
action = actor.decide_action(observation, episode)
# 行動a_tの実行により、s_{t+1}, r_{t+1}を求める
observation_next, _, done, _ = self.env.step(action)
# 報酬を与える
if done: # ステップ数が200経過するか、一定角度以上傾くとdoneはtrueになる
if step < 195:
reward = -1 # 失敗したので-1の報酬を与える
else:
reward = 1 # 成功したので+1の報酬を与える
else:
reward = 0
# Qテーブル, Vを更新する
update_Qtable_V(observation, action, reward, observation_next)
# 観測値を更新する。
observation = observation_next
"""途中までだよ"""
Sarsaと行動を決める部分も変更した。これによって得られた最後のエピソードは次のようになった。
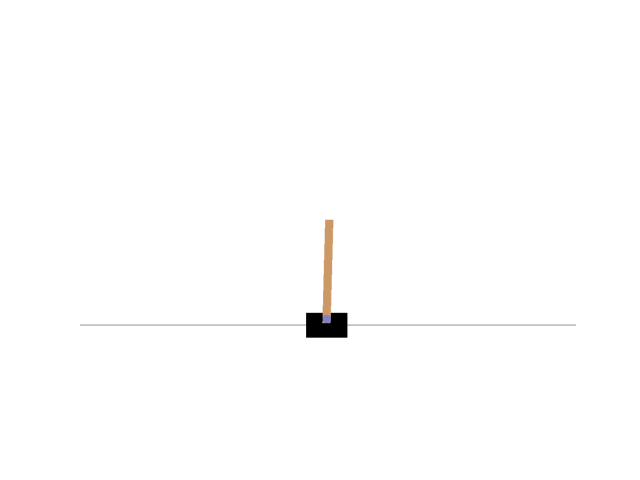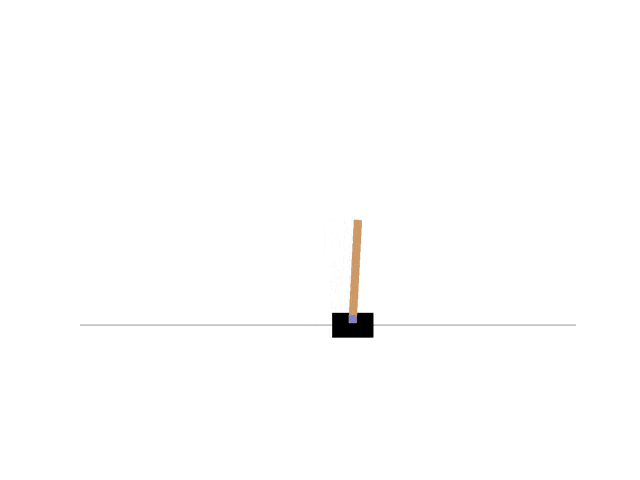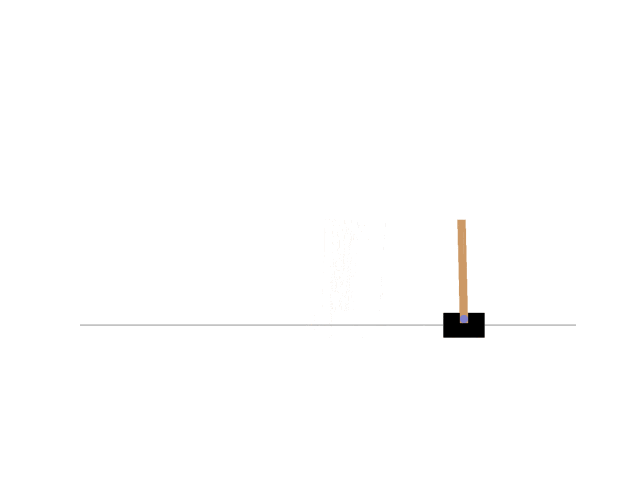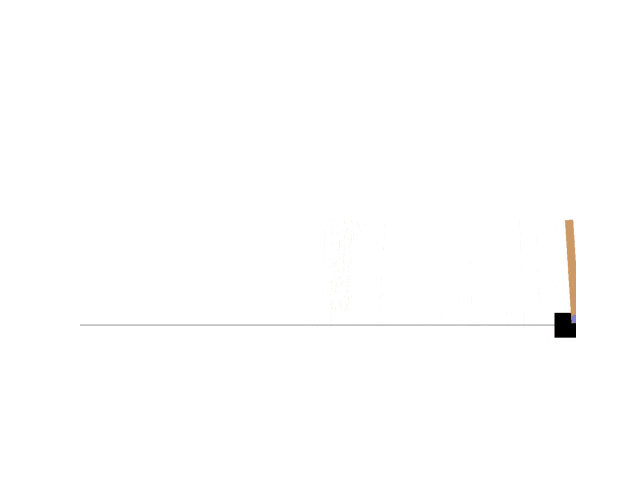
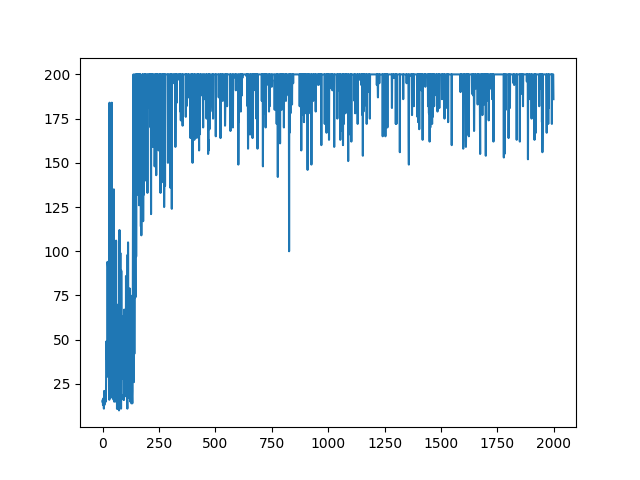
エピソードごとの報酬の遷移は以下のようになった。
直近100エピソードの報酬の平均およびそのばらつき(標準偏差)は以下のようになった。
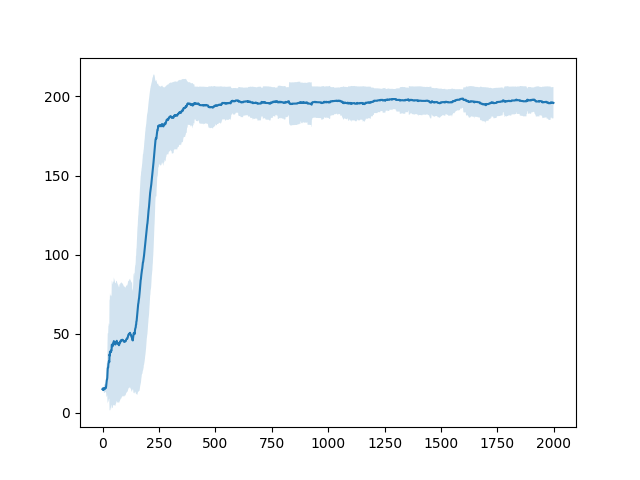
一つ目の図からGameAI Gym本来の学習終了が達成されなかったことがわかった。また、二つ目の図からこの手法が最も早く学習が収束したことがわかった。学習の収束とは学習終了の早さではなく、エピソード数に対する報酬の平均の増加の速さとした。