たたみ込みの理解

Christopher Olah氏のブログ記事
http://colah.github.io/posts/2014-07-Understanding-Convolutions/
の翻訳です。
翻訳の誤りなどあればご指摘お待ちしております。

---

以前の記事では、重要な数学について何も言及することなく、たたみ込みニューラルネットワークの理解を確立しました。しかし、さらに進むためには、たたみ込みを理解する必要があります。

単にたたみ込みニューラルネットワークを理解したいだけであれば、たたみ込みを大雑把に理解するだけで十分かもしれません。しかし、このシリーズの目的は、たたみ込みニューラルネットワークのフロンティアへ進み、新しい選択肢を探ることです。そのためには、たたみ込みをかなり深く理解する必要があります。

ありがたいことに、いくつかの例により、たたみ込みはかなり直接的なアイデアになります。

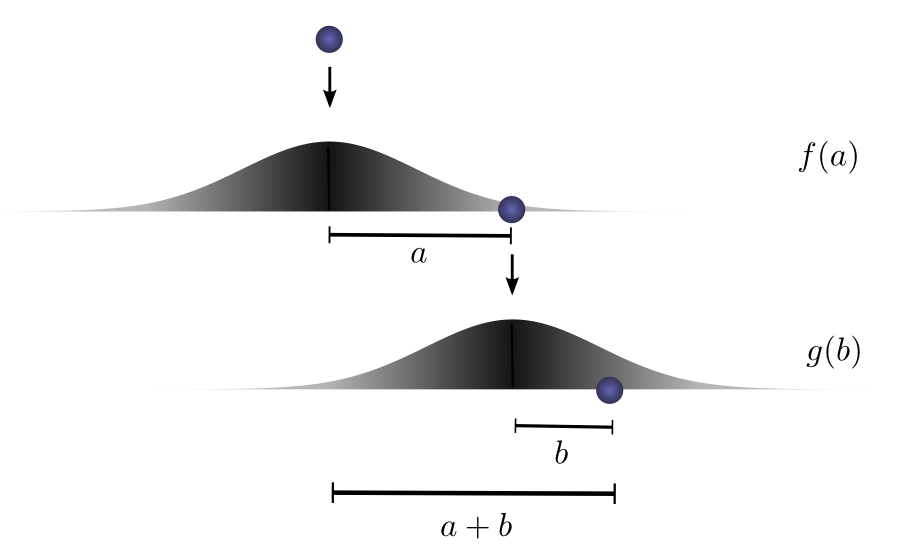
#落下するボールからの教え

ボールをある高さから地面に落とすと想像してください。ここでは１次元の運動を行うとします。ボールを落下させ、着地点の上から再びボールを落下させた場合、ボールが距離 $c$ 移動する可能性はどのくらいでしょうか？

ブレークダウンしてみましょう。最初の落下の後、開始点から $a$ 単位離れた点に着地する確率を $f(a)$ とします。ここで、$f$ は確率分布です。

最初の落下の後、ボールを拾い上げ、最初の着地点の上方の、別の高さから落下させます。新たな開始点からボールが $b$ 単位離れる確率を $g(b)$ とします。
異なる高さから落下させた場合、$g$ は異なる確率分布になるでしょう。

最初の落下の結果を固定し、ボールが距離 $a$ 移動したとした場合、ボールが総距離 $c$ 移動するためには、２回目の落下による移動距離は、$b$ に固定されます（ここで、$a+b=c$）。そして、これが起こる確率は単に $f(a)⋅g(b)$ です。¹

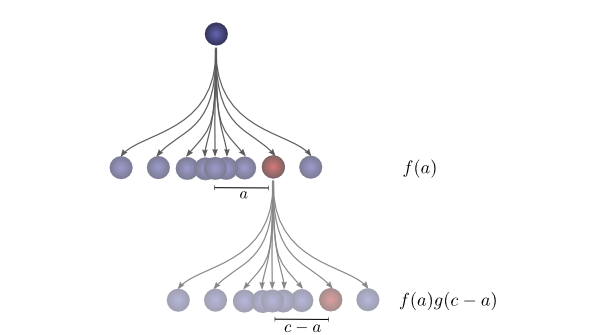
これについて特定の離散的な例で考えてみましょう。総距離 $c$ を $3$ にしたいとします。初回が $a=2$ だった場合、総距離 $a+b=3$であるためには２回目は $b=1$ でなければなりません。この確率は $f(2)⋅g(1)$ です。

しかし、これが総距離 $3$ になる唯一の方法ではありません。ボールは初回に $1$ 単位移動し、２回目に $2$ 移動するかもしれません。あるいは、初回が $0$ で２回目が $3$ かもしれません。合計 $3$ である限り、任意の $a$ と $b$ になり得ます。

確率はそれぞれ、$f(1)⋅g(2)$ および $f(0)⋅g(3)$ です。

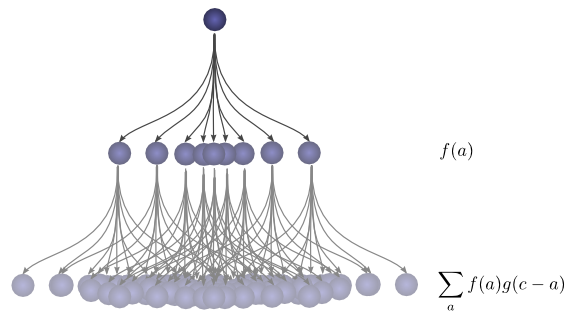
ボールが総距離 $c$ に到達する総合的な可能性を求めるためには、$c$ に到達する可能な方法のうち、１つを検討するだけでは不十分です。その代わりに、$c$ を２回の落下 $a$ と $b$ に分割するすべての可能な方法を考え、それぞれの方法の確率を合計します。

...  f(0)⋅g(3) + f(1)⋅g(2) + f(2)⋅g(1)  ...

$a+b=c$ の各ケースの確率が単に $f(a)⋅g(b)$ であることは、すでに見てきました。そこで、$a+b=c$ のすべての解にわたって合計し、全体の可能性を次のように表すことができます：

\sum_{a+b=c} f(a) \cdot g(b)

たたみ込みであることが判明しました！特に、$f$ と $g$ のたたみ込みの $c$ における値は、以下で定義されます：

(f\ast g)(c) = \sum_{a+b=c} f(a) \cdot g(b)~~~~

$b=c-a$ を代入すると、以下を得ます：

(f\ast g)(c) = \sum_a f(a) \cdot g(c-a)

これがたたみ込みの標準的な定義² です。

もう少し具体的にするために、ボールが着地する可能性のある位置の観点で考えることができます。最初の落下の後、中継位置 $a$ に確率 $f(a)$ で着地します。$a$ に着地した場合、位置 $c$ に着地する確率は $g(c-a)$ です。

たたみ込みを得るために、すべての中継位置を考えます。

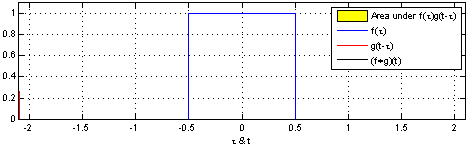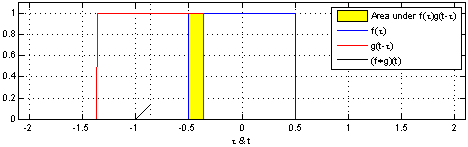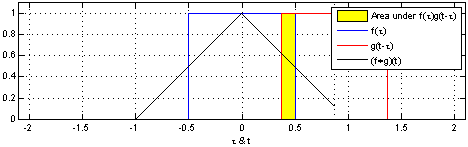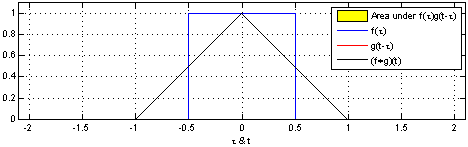
#たたみ込みの可視化

たたみ込みをより簡単に考えることができるとても素晴らしいトリックがあります。

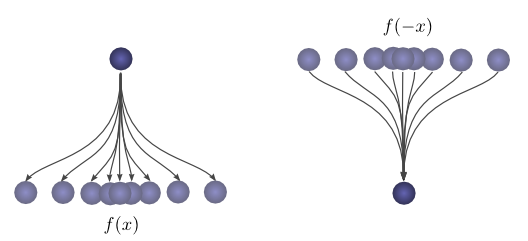
まず、観測です。ボールが開始点から特定の距離 $x$ に着地する確率を $f(x)$ とします。その時、着地した後、開始点が着地点から距離 $x$ の位置だった確率は $f(-x)$ です。

２回目の落下の後にボールが位置 $c$ に着地したことがわかっている場合、前の位置が $a$ であった確率はいくらでしょうか？

そう、前の位置が $a$ であった可能性は $g(−(a−c))=g(c−a)$ です。

次に、ボールが最終的に $c$ に着地することに寄与する中継位置それぞれの確率について考えます。最初の落下でボールが中継位置 $a$ に移動する確率は $f(a)$ です。また、ボールが $c$ に着地した場合、ボールが $a$ にいた確率は $g(c-a)$ です。

$a$ にわたって合計することで、たたみ込みを得ます。

このアプローチの利点は、値 $c$ におけるたたみ込みの評価が、単一の画像に視覚化可能になることです。下半分を周辺でシフトさせることにより、$c$ の他の値におけるたたみ込みを評価できます。これにより、全体としてたたみ込みを理解することができます。

例えば、分布が揃ったときに、それがピークに達することがわかります。

そして、分布の交わりが小さくなると、縮小します。

このトリックをアニメーションで使用することにより、実際に視覚的にたたみ込みを理解することが可能となります。

以下で、２つのボックス関数のたたみ込みを可視化することができます：

Wikipediaより

この観点により、多くの物事はより直観的になります。

確率的でない例を考えてみましょう。たたみ込みは時に音声操作で使用されます。例えば、エコーを生成するために、２つのスパイクを持ち、他の場所ではゼロである関数が使用されるかもしれません。ダブル-スパイク関数をスライドさせることにより、最初に１つのスパイクがある時点にヒットして出力音にその信号を追加し、後に、もう１つのスパイクが従って第２の遅延コピーを追加します。

#高次元のたたみ込み

たたみ込みは極めて一般的な考え方です。また、より高い次元で使用することができます。

それでは、再び落下するボールの例を考えてみましょう。ここでは、落下する時に、１次元ではなく、2次元でその位置がシフトします。

たたみ込みは以前と同様です：

(f\ast g)(c) = \sum_{a+b=c} f(a) \cdot g(b)

ただし、ここでは $a$、$b$、および $c$ はベクトルです。より明確にするために、

(f\ast g)(c_1, c_2) = \sum_{\begin{array}{c}a_1+b_1=c_1\\a_2+b_2=c_2\end{array}} f(a_1,a_2) \cdot g(b_1,b_2)

または標準的な定義で：

(f\ast g)(c_1, c_2) = \sum_{a_1, a_2} f(a_1, a_2) \cdot g(c_1-a_1,~ c_2-a_2)

１次元たたみ込みと同様に、１つの関数を別の関数の上でスライドさせ、掛けて足すこととして、２次元たたみこみを考えることができます。

１つの一般的な応用は、画像処理です。画像は２次元の関数として考えることができます。多くの重要な画像変換は、画像の関数に「カーネル」と呼ばれる非常に小さな、局所関数をたたみ込む、たたみ込みです。

River Trailの公式ドキュメントより

カーネルは、画像のすべての位置にスライドし、それがかぶさるピクセルの荷重和として新たなピクセルを計算します。

例えば、$3x3$ ピクセルのボックスを平均化することにより、画像をぼかすことができます。これを行うために、カーネルはボックス内の各ピクセルにおいて $1/9$ の値をとります。

GIMPの公式ドキュメントより引用

また、隣接する２つのピクセルで $-1$ と $1$ の値をとり、他の場所ではゼロとすることで、エッジを検出することができます。つまり、隣接する２つのピクセルの差分をとります。隣接するピクセルが類似している場合、これはほぼゼロになります。しかし、エッジでは、隣接するピクセルは、エッジに垂直な方向でかなり違っています。

GIMPの公式ドキュメントより引用

GIMPの公式ドキュメントには、他に多くの例があります。

#たたみ込みニューラルネットワーク

それで、たたみ込みはたたみ込みニューラルネットワークにどのように関連しているのでしょうか？

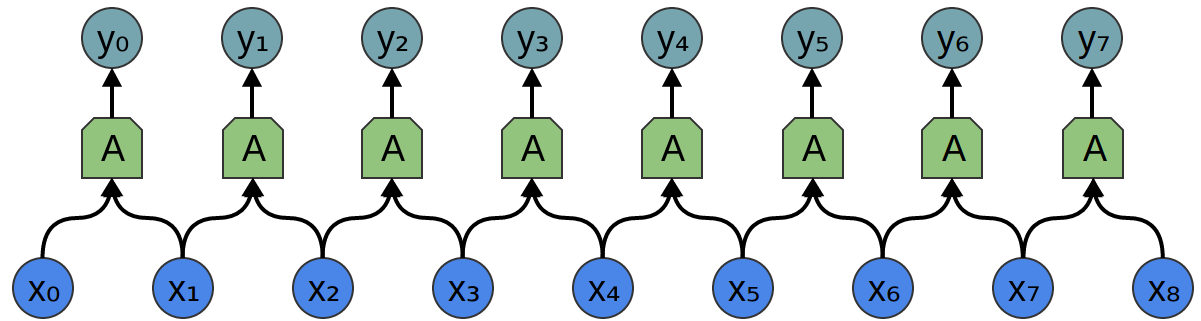
以前の記事で説明したような、入力 ${x_n}$ と出力 ${y_n}$ を持つ１次元のたたみ込み層を考えましょう：

以前述べたように、出力を入力の式として記述することができます：

y_n = A(x_{n}, x_{n+1}, ...)

一般的に、$A$ は複数のニューロンです。しかし、しばらくは１つのニューロンであると思ってください。

ニューラルネットワークにおける典型的なニューロンが以下で記述されることを思い出してください：

\sigma(w_0x_0 + w_1x_1 + w_2x_2 ~...~ + b)

ここで、$x_0$、$x_1$、 … は入力です。重み、$w_0$、$w_1$、 … はニューロンが入力に結合する方法を記述します。負の重みは入力がニューロンの発火を阻害することを意味し、正の重みは奨励することを意味します。重みは、ニューロンの心臓部であり、その振る舞いを制御します。³ 複数のニューロンが等価であるということは、それらの重みが同じであるということと同じです。

たたみ込みが扱うのは、すべての重みおよびどれが等価かを記述する、このニューロンの配線です。

一般的に、個々のニューロンではなく、同じ層のすべてのニューロンについて一度に記述します。トリックは重み行列 $W$ を持つことです：

y = \sigma(Wx + b)

例えば、以下を得ます：

y_0 = \sigma(W_{0,0}x_0 + W_{0,1}x_1 + W_{0,2}x_2 ...)

y_1 = \sigma(W_{1,0}x_0 + W_{1,1}x_1 + W_{1,2}x_2 ...)

行列の各行は、ニューロンとその入力を結合する重みを記述します。

たたみ込み層に戻ると、しかし、同じニューロンの複数のコピーがあるため、多くの重みが複数の位置に現れます。

そしてそれは等式に対応します：

y_0 = \sigma(W_0x_0 + W_1x_1 -b)

y_1 = \sigma(W_0x_1 + W_1x_2 -b)

通常、重み行列はすべての入力とすべてのニューロンを異なる重みで結合します：

W = \left[\begin{array}{ccccc} 
W_{0,0} & W_{0,1} & W_{0,2} & W_{0,3} & ...\\
W_{1,0} & W_{1,1} & W_{1,2} & W_{1,3} & ...\\
W_{2,0} & W_{2,1} & W_{2,2} & W_{2,3} & ...\\
W_{3,0} & W_{3,1} & W_{3,2} & W_{3,3} & ...\\
...     &   ...   &   ...   &  ...    & ...\\
\end{array}\right]

上記のようなたたみ込み層の行列は非常に異なって見えます。同じ重みがたくさんの位置に現れます。そして、ニューロンは多くの可能な入力と結合していないため、多くのゼロがあります。

W = \left[\begin{array}{ccccc} 
w_0 & w_1 &  0  &  0  & ...\\
 0  & w_0 & w_1 &  0  & ...\\
 0  &  0  & w_0 & w_1 & ...\\
 0  &  0  &  0  & w_0 & ...\\
... & ... & ... & ... & ...\\
\end{array}\right]

上記の行列を掛けることは、$[...0, w_1, w_0, 0...]$ とたたみ込むことと同じです。異なる位置にスライドする関数は、その位置にニューロンを持つことに対応します。

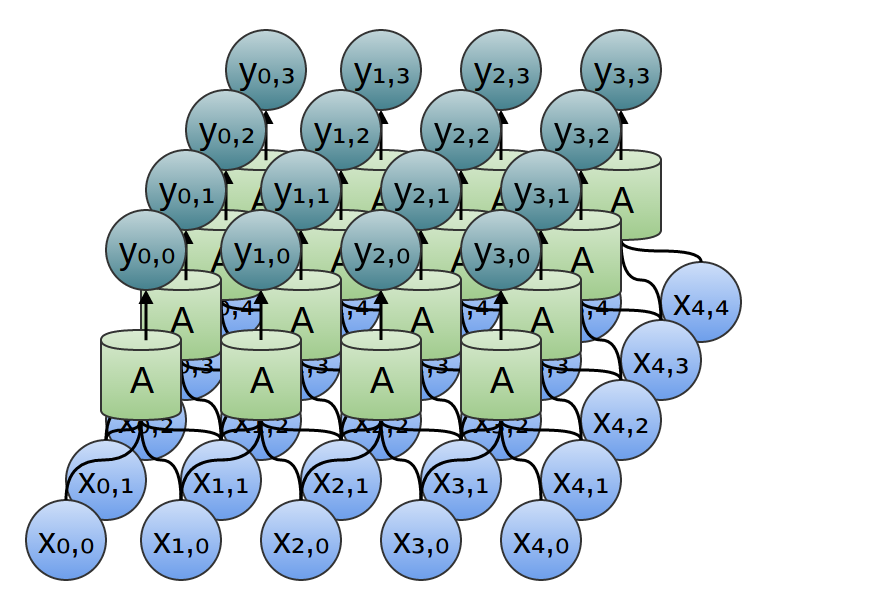
２次元のたたみ込み層についてはどうでしょうか？

２次元たたみ込み層の配線は２次元のたたみ込みに相当します。

カーネルを周辺にスライドさせ、すべてのパッチに適用することにより画像のエッジを検出する、上記のたたみ込みの例を考えてみましょう。このように、たたみ込み層は、画像のすべてのパッチにニューロンを適用します。

#結論

このブログ記事では多くの数学的な機構を紹介してきましたが、得られたものは明らかではないかもしれません。たたみ込みは明らかに確率論とコンピュータグラフィックスにおいて有用なツールですが、たたみ込みの観点からたたみ込みニューラルネットワークを言い表すことから、何が得られるでしょうか？

第１の利点は、ネットワークの配線を記述するためのいくつかの非常に強力な言語を持つことが出来るということです。この利点を明確にするには、私たちが扱ってきた例は十分に複雑ではありません。しかし、たたみ込みにより、膨大な量の不快な記述を避けることができます。

第２に、たたみ込みにより、重要な実装上の利点が付随します。多くのライブラリは非常に効率的なたたみ込みルーチンを提供します。さらに、たたみ込みは単純には $O(n^2)$ の演算のように見えますが、いくつかのかなり深い数学的洞察を使用することにより、$O(n\log(n))$ で実装することが可能です。これについては、今後の記事でもっと詳細に説明するつもりです。

実際、GPU上の高効率な並列たたみ込みの実装を使用することが、コンピュータビジョンの近年の進歩に不可欠でした。

#このシリーズの次の記事

この記事は、たたみ込みニューラルネットワークとその一般化のシリーズの一部です。最初の２つの記事は、ディープラーニングに精通した方のためのレビューですが、最後の１つは、誰にでも興味があるもののはずです。最新版を得るためには、私のRSSフィードを購読してください！

下または横にコメントしてください。github 上でプルリクエストすることができます。

#謝辞

たたみ込みについての広範な議論をし、この記事の執筆の手助けをしてくださった、Eliana Lorch に深く感謝しています。

また、コメントし、支援をしてくださった、Michael Nielsen と Dario Amodei に感謝いたします。

1. 私たちは、最初にボールが $a$ 単位移動し、２回目に $b$ 単位移動する確率を求めています。分布 $P(A)=f(a)$ と $P(b)=g(b)$ は共に、中心 $0$ で、独立しています。そのため、$P(a,b) = P(a) * P(b) = f(a) \cdot g(b)$ です。 ↩

2. 私がこれまで見たことが無い、この標準的でない定義は、多くの利点を持っているようです。今後の記事で、この定義は新たな代数構造へ一般化するために役立つため、非常に有用であることがわかります。それはまた、たたみ込みの多くの代数的性質を本当に明白にするという利点を持っています。
   たとえば、たたみ込みは可換演算です。すなわち、$f\ast g = g\ast f$ です。なぜならば、
   $\sum_{a+b=c} f(a) \cdot g(b) ~~=~ \sum_{b+a=c} g(b) \cdot f(a)$
   たたみ込みはまた、結合的です。すなわち、$(f\ast g)\ast h = f\ast (g\ast h)$ です。なぜならば、
   $\sum_{(a+b)+c=d} (f(a) \cdot g(b)) \cdot h(c) ~~=~ \sum_{a+(b+c)=d} f(a) \cdot (g(b) \cdot h(c))$ ↩

3. ニューロンが発火するかどうかの「しきい値」であるバイアスもあります。しかし、これははるかに簡単です。また、これついて述べることでこのセクションを乱雑にしたくありません。 ↩