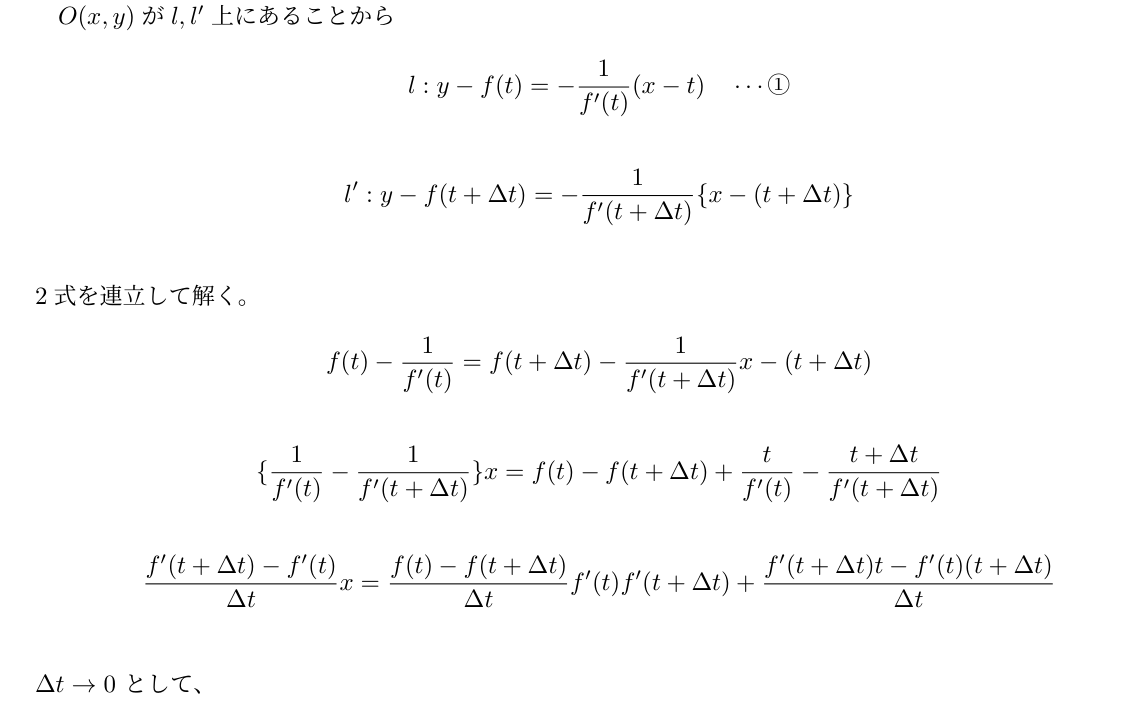はじめに
PhysiKyu Advent Calendar 10日目です!今日は曲率半径の話をします。
曲率半径の意味
曲線の微小部分を上図のように円弧で近似することを考えます。曲率半径は、この円の半径を意味します。よって、曲率半径は、大きければ曲線の曲がり具合は小さく、逆に小さければ曲がり具合は大きくといった感じで曲線の曲がり具合を表す量となっています。また、この曲率半径の逆数をとったものを曲率といいます。
曲率半径を求めよう➀
次は、曲率半径を実際に求めていきます。ここでは、物体の運動の軌道について曲率半径を考えます。
物体が時間$d t$の間に点$P$から点$P\prime$に移動する状況を考えます。
このとき、軌道の微小部分を円弧で近似する。半径$\rho$、中心角$d\theta$とすると、軌道の微小部分の長さ$d s$について、
$$\rho = \frac{ds}{d\theta}$$
$$=\frac{ds/dt}{d\theta/dt}$$
$$=\frac{v}{d\theta/dt}$$
ここで$\frac{d\theta}{dt}$を物体の速度$\mathbf v$と加速度$\mathbf a$を用いて書き直すことを考えます。
$$\frac{d\theta}{dt}=|\frac{d}{dt}(\frac{\mathbf v}{v})|$$
$$=\frac{|\mathbf a v-\dot v\mathbf v|}{v^2}$$
よって、
$$\rho=\frac{v^3}{|\mathbf a v-\dot v \mathbf v|}$$
このように曲率半径が求められました。
曲率半径を求めよう➁
次は上でやったのとは別の方法で曲率半径を導出しようと思います。
考える状況は以下の通りです。
曲線$y=f(x)$上の2点$P$、$P'$における$s$の法線を$l$,$l'$として、この2つの直線の交点を点$O$とします。ここで、点$P'$を点$P$に限りなく近づけたときの線分$OP$の長さを求めます。

これは$P(t,f(t))$、$P'(t+\Delta t,f(t+\Delta t))$として$\Delta t \rightarrow0$を考えることで求められます。計算が煩雑なので途中過程は最後に載せておきます。
$$OP=\frac{[1+{f'(t)}^2]^\frac{3}{2}}{|f''(t)|}(=\rho)$$
考えた状況からここで求めたものが曲率半径$\rho$であると分かります。
まとめ
今回は二つの方法から曲率半径の式を求めて、それぞれ違う形の式が得られました。実はこれらの式は変形していくことでちゃんと同じ式に表されます。この内容は近いうちに「曲率半径の話Ⅱ」としてまとめて投稿したいと考えてます!
以上です。ありがとうございました!
参考にした文献・サイト
・基幹講座物理学 力学 篠本磁、坂口英継
・高校数学の美しい物語 曲率・曲率半径の感覚的な意味と求め方
https://manabitimes.jp/math/952