記述統計編の続きです
推測統計編
11講 母集団と統計的推定
12講 母分散
(無限)母集団のいくつかのデータから、徐集団全体について何らかの推測を行う（＝部分から全体への推論）
例：味噌汁の味見とか
母集団の平均値μを母平均という $ μ＝データの数値×相対度数の和 $
母集団に対しても、標準偏差を計算することで、母集団に「どんなふうにデータが詰まっているのか」がより詳しく分かる
13講 標本平均
複数のデータを観測し、その平均をとったものを標本平均と呼ぶ
大数の法則
nが大きければ大きいほど、標本平均は母平均に近い数値をとる可能性が高くなる
14講,15講 信頼区間
母集団の分布と標準偏差
母集団の平均をμ、標準偏差をσとしたとき、そこから観測されるデータxのn個に対する標本平均 $ \bar{x} $ の分布は正規分布
$ \bar{x} $の平均値はμのままだが、標準偏差は $ \frac{σ}{\sqrt{n}} $となる
└広がり具合は$ \frac{1}{\sqrt{n}} \ $となり、そそり立つような形になる。
└平均に近い値は多く観測され、平均から遠い値ほどなかなか観測されなくなるため
標準偏差が変わるので、信頼区間も変わる
- 正規分布のデータn個の標本平均$ \bar{x} $に対する95%信頼区間は $ (μ-1.96\frac{σ}{\sqrt{n}}) $以上＋$ (μ+1.96\frac{σ}{\sqrt{n}}) \ $以下
- 平均値μ、標準偏差σの正規分布に従うn個の標本平均$ \bar{x} $に対する95%信頼区間は、
以下の不等式を解いて得られる範囲
-1.96≦\frac{\bar{x}-μ}{\frac{σ}{\sqrt{n}}}≦+1.96
16講 カイ二乗分布
標本分散
標本分散は$ s^2 $で表す（母分散$ σ^2 \ $とは異なる)
└各標本に対して $ 標本n-\bar{x}$で偏差をつくり、各偏差の2乗をnで割る
└イメージ図は標本平均の時と同じような感じ
カイ二乗分布
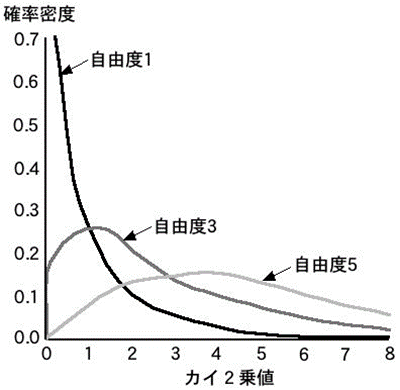
- 0付近のデータの相対度数が大きい
- 自由度nが大きくなるにしたがって、傾斜が緩やかになる&山の頂点が右にずれてく
- 0以上の値しか出てこない
- 標準正規母集団からのnこの標本から統計量Vを作ると、Vは自由度nのカイ二乗分布をする
$ V = {x_1}^2 + {x_2}^2 + ... + {x_n}^2 $
17講 母分散を推定する(μを知ってる場合)
- 母分散もカイ二乗分布で推定できる
- 母平均μを知っている場合： $ V = (\frac{x_1-μ}{σ})^2 + (\frac{x_2-μ}{σ})^2 + ... + (\frac{x_n-μ}{σ})^2\ $
- 信頼区間を求めるにはカイ二乗分布の分布表を参照し、$ a≦V≦b $の不等式の$ σ^2 \ $ を解く
18講 標本分散の分布
19講 母分散を推定(μが未知)
統計量Wの定義
$ W = (\frac{x_1-\bar{x}}{σ})^2 + (\frac{x_2-\bar{x}}{σ})^2 + ... + (\frac{x_n-\bar{x}}{σ})^2 = \frac{n×s^2}{σ^2}\ $
Wは自由度-1のカイ二乗分布に従う
母分散を推定する手順
- 標本平均$ \bar{x}\ $を計算
- 偏差を作り、その2乗和をnで割って標本分散$ s^2\ $を計算
- 計算した標本分散をもとに、Wを計算（$ \frac{n×s^2}{σ^2}\ $）
- 自由度n-1の95%信頼区間を調べ、不等式を解く
20講,21講 t分布
$ T = \frac{(\bar{x}-μ)\sqrt{n-1}}{s} \ $は自由度(n-1)のt分布に従う。
t分布は山なりの正規分布に似た形で、相対度数がわかっている分布。
t分布による推定の手順
- 標本平均$ \bar{x}\ $と標本標準偏差$ s $を計算
- 統計量Tを計算（例：$ \frac{(80-μ)\sqrt{5}}{3.51} $ みたいな感じの値ができればOK）
- 自由度n-1の95%信頼区間を調べ、不等式を解く