完全独習 統計学入門を読んで

統計学入門を読んで

小学生の読書感想文のようなタイトルとなりましたが、書籍を読んで自分用にまとめたメモです。

完全独習　統計学入門 - 小島 寛之(著)

評判が良いことは知っていたのですが、みんなが奨めるものは気が進まないという悪癖があり、ずっと読んでいませんでした。
しかし上司に勧められた＆中学数学までで説明されている＆安いというのに惹かれ読んだところ、とてもよかったので備忘もかねてメモを残します。

以下x講は書籍と対応させており、それに要約文のタイトルを併記しました。
本書は理解を深めさせるための章,講が多く設けられていますが、本記事は振り返り用のメモであるため省略しました。
（理解を深めるためにはとてもよかったので、もし読んでない方がいらしたらぜひ読んでみてください）

0講 記述統計と推測統計

※本書では確率を扱わない
※中学数学までで理解できるように書いてある（Σとか使わない）

1. 記述統計：
   
   　得られたデータからその特徴を抜き出す
   
   　└度数分布表やヒストグラムなどのグラフ
   
   　└平均や標準偏差などの統計量による方法論
   
2. 推測統計：
   
   　統計学の手法と確率理論をミックス。部分から全体を推測する
   
   　└全体を把握しきれないほど大きな対象を推測
   
   　└まだ起きておらず、未来に起きることを推測
   

記述統計編

1講 度数分布表とヒストグラム

1. 例えば、女子大生の身長は皆同じではなく、様々な値をとっている。→これを分布するという。
2. 分布が生じるのは、数値が決まる背後に何らかの不確実性が働いているから。
3. この不確実性には、様々た__特徴や癖__があることがわかっており、これを分布の特性と呼ぶ。
4. 分布との特性を見るには、統計量{:特徴を代表させる値)やヒストグラムで確認すると良い。
   
   着眼点の例
   
   └データがどこに集中しているか
   
   └データに対称性がありそうか

2講 平均値　
3講 分散

平均値=階級値×相対度数の合計
column ※2つの値x,yの平均を出したい場合
算術平均(合計の平均など)　　　　　：　足して個数で割る
幾何平均(成長率を平均するときなど)：　$ \sqrt{xy}\ $
二乗平均(標準偏差など)　　　　　　：　$ \sqrt{\frac{(x^2+y^2)}{2}}\ $
調和平均(速度の平均など)　　　　　：　$ \frac{2}{\frac{1}{x}+\frac{1}{y}}　\ $

偏差：各データが平均値からどのくらい大きい/小さいか
分散：偏差の2乗の合計/個数
※二乗にするのは、大きいほうにはなれようが、小さいほうにはなれようが打ち消しあわないようにどちらも正の数として評価するため。
標準偏差：偏差の2乗平均 = 分散のルート

4講 標準偏差はデータの特殊性がわかる　
5講,6講 標準偏差の理解を深める(省略)　
7講 正規分布

正規分布の特徴

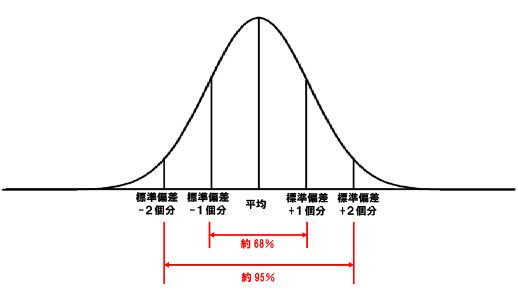
縦軸：相対度数（どの階級も度数は無限＝度数そのものは無視して、相対度数でヒストグラムを作る）
横軸：階級値

• 標準正規分布:　　平均=0, 標準偏差=1
• 一般の正規分布:　平均=μ, 標準偏差=σ
  
  └一般の正規分布のデータ=σ×標準正規分布のデータ+μ

$ \frac{データ-平均値}{標　準　偏　差} \ $ と加工すると、平均値0,標準偏差1となり標準化できる
（一般の正規分布を標準正規分布になおせる）

8講 95%信頼区間　
9講 仮説検定　
10講 区間推定

※本書では95%予言的中区間という言葉を用いている

• 標準正規分布の95%信頼区間は-1.96以上＋1.96以下
• 正規分布の95%信頼区間は(μ-1.96σ)以上＋(μ+1.96σ)以下
• データxが、平均値μ、標準偏差σの正規分布に従う場合の95%信頼区間は、
  以下の不等式を解いて得られる範囲

-1.96≦\frac{x-μ}{σ}≦+1.96

• この不等式が成立しない場合、仮説は棄却される

95パーセント予言的中区間というのは、
「もう傾向知ってるから、95％の確率でこんくらいの数字になるね」
と予言している区間のことです。

95パーセント信頼区間というのは、
「傾向知らんけど、こんくらいの幅で予想してったらそん中の95％は当たってるはずやで」
と信頼できる区間のことです。
※1つの幅データのうちの95％が合ってるんじゃなくて、
　そういう幅データで計測してったらそのうちの95％には狙った真値が入っているという意味
--引用元：予言的中区間と信頼区間の違いを簡単に説明したい

推測統計編

11講 母集団と統計的推定　
12講 母分散

(無限)母集団のいくつかのデータから、徐集団全体について何らかの推測を行う（＝部分から全体への推論）
例：味噌汁の味見とか

母集団の平均値μを母平均という $ μ＝データの数値×相対度数の和 $
母集団に対しても、標準偏差を計算することで、母集団に「どんなふうにデータが詰まっているのか」がより詳しく分かる

13講 標本平均　

複数のデータを観測し、その平均をとったものを標本平均と呼ぶ

大数の法則

nが大きければ大きいほど、標本平均は母平均に近い数値をとる可能性が高くなる

14講,15講 信頼区間

母集団の分布と標準偏差

母集団の平均をμ、標準偏差をσとしたとき、そこから観測されるデータxのn個に対する標本平均 $ \bar{x} $ の分布は正規分布
$ \bar{x} $の平均値はμのままだが、標準偏差は $ \frac{σ}{\sqrt{n}} $となる
└広がり具合は$ \frac{1}{\sqrt{n}} \ $となり、そそり立つような形になる。
└平均に近い値は多く観測され、平均から遠い値ほどなかなか観測されなくなるため

標準偏差が変わるので、信頼区間も変わる

• 正規分布のデータn個の標本平均$ \bar{x} $に対する95%信頼区間は $ (μ-1.96\frac{σ}{\sqrt{n}}) $以上＋$ (μ+1.96\frac{σ}{\sqrt{n}}) \ $以下
• 平均値μ、標準偏差σの正規分布に従うn個の標本平均$ \bar{x} $に対する95%信頼区間は、
  以下の不等式を解いて得られる範囲

-1.96≦\frac{\bar{x}-μ}{\frac{σ}{\sqrt{n}}}≦+1.96

16講 カイ二乗分布

標本分散

標本分散は$ s^2 $で表す（母分散$ σ^2　\ $とは異なる)
└各標本に対して $ 標本n-\bar{x}$で偏差をつくり、各偏差の2乗をnで割る
└イメージ図は標本平均の時と同じような感じ

カイ二乗分布

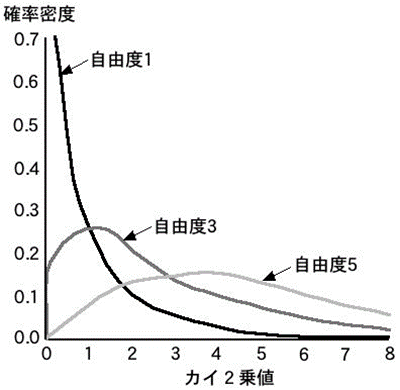
• 0付近のデータの相対度数が大きい
• 自由度nが大きくなるにしたがって、傾斜が緩やかになる&山の頂点が右にずれてく
• 0以上の値しか出てこない
• 標準正規母集団からのnこの標本から統計量Vを作ると、Vは自由度nのカイ二乗分布をする
  
  　 $ V = {x_1}^2 + {x_2}^2 + ... + {x_n}^2 $

17講 母分散を推定する(μを知ってる場合)

• 母分散もカイ二乗分布で推定できる
  
• 母平均μを知っている場合： $ V = (\frac{x_1-μ}{σ})^2 + (\frac{x_2-μ}{σ})^2 + ... + (\frac{x_n-μ}{σ})^2\ $
  
• 信頼区間を求めるにはカイ二乗分布の分布表を参照し、$ a≦V≦b $の不等式の$ σ^2 \ $ を解く
  

18講 標本分散の分布　
19講 母分散を推定(μが未知)

統計量Wの定義

$ W = (\frac{x_1-\bar{x}}{σ})^2 + (\frac{x_2-\bar{x}}{σ})^2 + ... + (\frac{x_n-\bar{x}}{σ})^2 = \frac{n×s^2}{σ^2}\ $
Wは自由度-1のカイ二乗分布に従う

母分散を推定する手順

1. 標本平均$ \bar{x}\ $を計算
2. 偏差を作り、その2乗和をnで割って標本分散$ s^2\ $を計算
3. 計算した標本分散をもとに、Wを計算（$ \frac{n×s^2}{σ^2}\ $）
4. 自由度n-1の95%信頼区間を調べ、不等式を解く

20講,21講 t分布

$ T = \frac{(\bar{x}-μ)\sqrt{n-1}}{s} \ $は自由度(n-1)のt分布に従う。
t分布は山なりの正規分布に似た形で、相対度数がわかっている分布。

t分布による推定の手順

1. 標本平均$ \bar{x}\ $と標本標準偏差$ s $を計算
2. 統計量Tを計算（例：$ \frac{(80-μ)\sqrt{5}}{3.51} $ みたいな感じの値ができればOK）
3. 自由度n-1の95%信頼区間を調べ、不等式を解く