数学の言葉がわからない、数式が読めないと困ったので、基礎から勉強しています。
本記事はその取り組みの一部で、正確に理解するというよりかは数式に直面したり、言葉を聞いてイメージができるようになることを目標としています。
前提知識:
- 中学数学
- データサイエンスに必要な数学基礎
追記 業務中度々混乱してしまったので小学生の範囲ですが、割合の定義
割合とは「ある量をもとにして、比べられる量がもとにする量の何倍にあたるかを表したもの」、また「もとにする量を 1 としたときの比べられる量の大きさを表したもの」です。
微分とは
- 傾き(=変化の割合)を求める操作
- 変数の微小な変化に対応する、関数の変化量を求めること
微分の使われどころ
例:単層のニューラルネットワーク
式で書くとこんな感じ
y=\sum_{k=1}^{n} w_k x_k +b\ \\
つまり何をやっているのか…
-
【学習フェーズ】
$ y= \underbrace{w_1x_1 + w_2x_2 + \cdots + w_nx_n +b}_{モデル=数式のこと} \hspace{1pt} $
のwの値をyが正解の値に近づくように微分で調整しながら、一番良いモデルを作る -
【推測フェーズ】
モデルができたら、wとbは定数にする。xを変数として、yを求める。
ということをやってる。
微分を表現するのに使う記号:limit
$ y = f(x) $に対する接線の傾きは $ f'(x) $と表すことができる(導関数という)
これを求めるのに極限(limit)を使う
参考講義:https://youtu.be/Y-1TR_ni85U?si=qHgoHkMpcwqsfXGn
$ f'(x) = lim_{h \to 0}\frac{f(x+h) - f(x)}{h} \hspace{1pt} $
$ lim_{h\to0} $は$ h $を限りなく$ 0 $に近づけるということ。
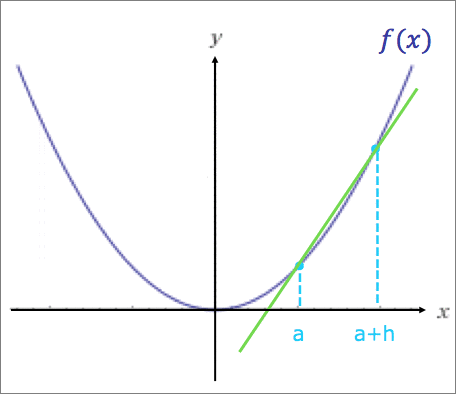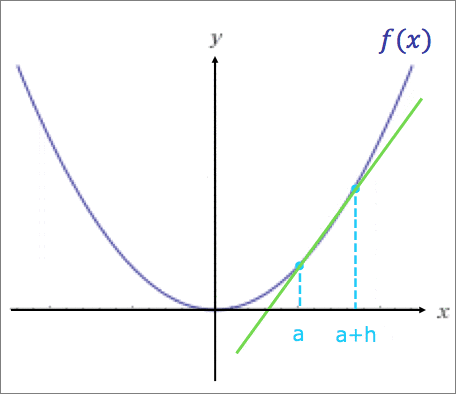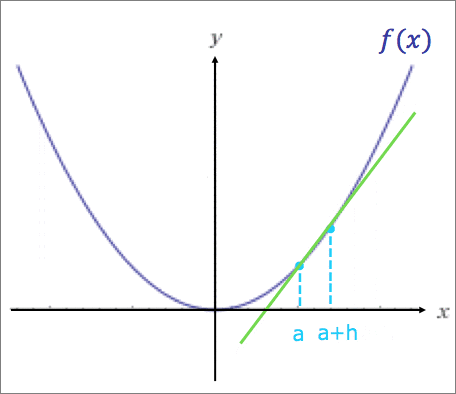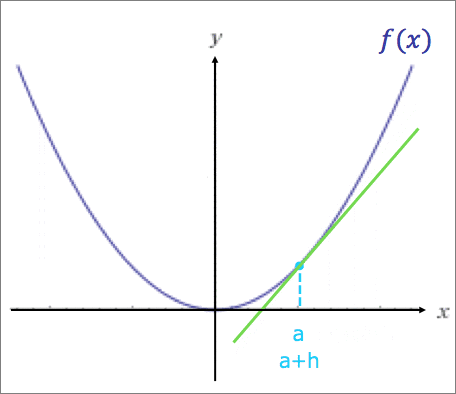
イメージ:
関数f(x)のx=aの点とx=a+hの点を結ぶ直線の、x+hをxに近づける(=hを0に近づける)
引用:【3分で分かる!】微分の計算のやり方・導関数の意味と求め方をわかりやすく
微分の公式
参考講義:https://youtu.be/SAZYMVGAiRM?si=YwanmZw4EfyhXElo
\begin{align}
y=f(x), \hspace{5pt} c:定数, \hspace{5pt} e:ネイピア数\\\\
y=c \hspace{10pt}→\hspace{10pt}f'(x) = \overbrace{(c)'}^{cの微分値という意味} = 0\hspace{5pt}\\
y=x \hspace{10pt}→\hspace{10pt}f'(x) = (x)'= x\hspace{5pt}\\
y=x^2 \hspace{5pt}→\hspace{5pt}f'(x) = (x^2)' = 2x\\
\end{align}
y=e^x \hspace{5pt}→\hspace{5pt}f'(x) = (e^x)' = e^x\\
y=e^{-x} \hspace{1pt}→\hspace{1pt}f'(x) = (-e^x)' = -e^x \\
※ネイピア数は微分しても値が変わらない
合成関数
合成関数とは、$ y=f(u), \ u=g(x) $のように、複数の関数の合成で表される関数のこと。
連鎖率
微分を分数で表現したものは以下のようにあらわすことができる。
合成関数を微分するときはこれを使う。
\frac{dy}{dx} = \frac{dy}{du}\frac{du}{dx}
シグモイド関数
yが0から1の間に収まる
シグモイド曲線は、こんな感じにS字のグラフになる

それを微分すると山なりのグラフになる(微分するときに合成関数を使う)
使われどころ:
勾配降下法、誤差逆伝播法でパラメーターの更新に使う
多変数関数と偏微分
$ y=f(x) $ x:独立変数、y:従属変数
$ y=f(x,y) $ 独立変数が2つ以上 ⇒多変数関数
使いどころ:
損失関数、誤差関数
勾配降下法→底のほう(小さいほう)に進むにはどうすればよいか計算する
偏微分
多変数関数を微分するときに、1つの変数にだけを変動させて、それ以外は定数として扱うこと
参考
【3分で分かる!】微分の計算のやり方・導関数の意味と求め方をわかりやすく
微分とは何か? - 中学生でも分かる微分のイメージ
シグモイド関数を理解してみる