困りました
仕事をしていて、数式が読めない&数学の言葉がわからなくて困ったので、基礎からやり直しをしています。本記事はそのまとめの一部です。
- 前提知識:中学数学程度
- 定義とかで逃れられない数式は備忘のために記載しました
- 言葉を聞いたときにグラフの形をイメージできることを目標としました
関数とは
x → 函数 → y
xを入力し、yの値が一つに決まる = yはxの関数である。
以下のようにあらわす
y = f(x)
一次関数
y = ax + b
- xとyの関係を直線で表すことができる
- 傾き(勾配):xが1進んだ時にyがどれだけ増えるか
- 切片:x=0の時のyの値

二次関数
使いどころの例:勾配降下法
正解と推定値の誤差を二次関数で近似し、頂点が最も誤差が少ないところとして、差が小さくなる方向(頂点に向かって)に進めていく
- (青のグラフ)下に凸; 最小値をとる場所を探すときに使用 例:$ y=x^2+3\ $
- (赤のグラフ)上に凸; 最大値をとる場所を探すときに使用 例:$ y= -x^2+2\ $
平方根とは
10 × 10 = 100\\
\sqrt{100} = 10\\\\
x^2 \cdots\cdots ①\\
\sqrt[n]{x}\cdots\cdots ②
①…$ x $を底(テイ)、$ ^2 $を指数と呼ぶ
②…累乗根。
指数関数
y = a^x\\
a: 底(a>0, a≠1)\\
x:指数\hspace{55pt}
- (グラフに表示したような増え方を)指数関数的に増大するという
- 0以上1未満は左右が逆になる
対数関数
使いどころ:尤度(物事の起こりやすさ), クロスエントロピー
y = log_ax\\
a: 底, x:真数, y:対数
- (青のグラフ) $ y=-log_3x $
- (赤のグラフ) $ y=log_2x $
自然対数の底 e:ネイピア数
自然対数:eを底とする対数のこと
e = \lim_{n \to \infty} \bigg(1+\frac{1}{n}\bigg)^2 \\
- $ y = e^x $は微分しても同じ数になる。 $ e^x $はexp(x)と書いたりもする。
- グラフのイメージは対数関数とだいたい同じ
数列と記号
- 等差数列 $ a1, a2, a3, \cdots , an $ a1とa2の差(公差)が一定
- 等比数列 $ a1, a2, a3, \cdots , an $ a1とa2の比(公比)が一定
- 総和: $ a1 + a2 + a3 + \cdots + an = \sum_{k=1}^{n} ak \ $
- 総乗: $ a1 \times a2 \times a3 \times \cdots \times an = \pi_{k=1}^{n} ak \ $
Σの使いどころ:ニューラルネットワーク
確率を少しだけ理解するための記事です。
確率とは
偶然性がある事象が発生する可能性のこと
確率 = ある事象が発生する場合の数 / 起こりうるすべての場合の数
いくつかの事象の起こりやすさがすべて等しいとき、「同様に確からしい」という
| 独立 | お互いの結果が影響しあうことがない時、二つの事象は独立であるといいます。二つの事象が独立である場合、二つの事象が同時に起こる確率はそれぞれの事象の確立の席で計算できます |
| 条件付き確率 | このとき、P(B|A)は「Aという条件のもとでBが起こる確率」を、P(A∩B)は「AかつBが起こる確率」を、P(A)は「Aが起こる確率」を表します。 |
| 期待値 |
順列
nの中からr個選んで並べる(順番も考慮する)
_nP_r = \frac{n!}{(n-r)!}\\
例:五人の中から3人を選んで並べる
_5P_3 = \frac {5!}{(5-3)!}=\frac{5\times4\times3\times2\times1}{2\times1} = 60 \
組み合わせ
nの中からr個選んで並べる(順番は関係ない)
_nC_r = \frac{n!}{r!(n-r)!} \\
例:五人の中から3人を選ぶ組み合わせ
_5P_3 = \frac {5!}{3!(5-3)!}=\frac{5\times4\times3\times2\times1}{3\times2\times1\times2\times1} = 10 \
微分とは
- 傾き(=変化の割合)を求める操作
- 変数の微小な変化に対応する、関数の変化量を求めること
微分の使われどころ
例:単層のニューラルネットワーク
式で書くとこんな感じ
y=\sum_{k=1}^{n} w_k x_k +b\ \\
つまり何をやっているのか…
-
【学習フェーズ】
$ y= \underbrace{w_1x_1 + w_2x_2 + \cdots + w_nx_n +b}_{モデル=数式のこと} \hspace{1pt} $
のwの値をyが正解の値に近づくように微分で調整しながら、一番良いモデルを作る -
【推測フェーズ】
モデルができたら、wとbは定数にする。xを変数として、yを求める。
ということをやってる。
微分を表現するのに使う記号:limit
$ y = f(x) $に対する接線の傾きは $ f'(x) $と表すことができる(導関数という)
これを求めるのに極限(limit)を使う
参考講義:https://youtu.be/Y-1TR_ni85U?si=qHgoHkMpcwqsfXGn
$ f'(x) = lim_{h \to 0}\frac{f(x+h) - f(x)}{h} \hspace{1pt} $
$ lim_{h\to0} $は$ h $を限りなく$ 0 $に近づけるということ。
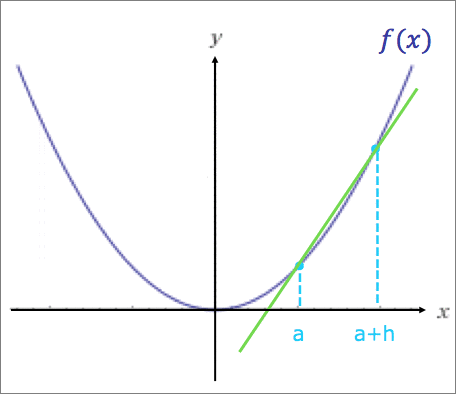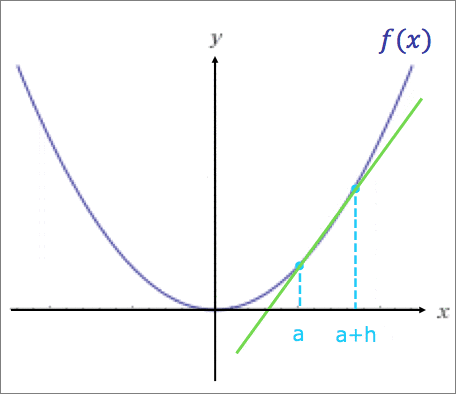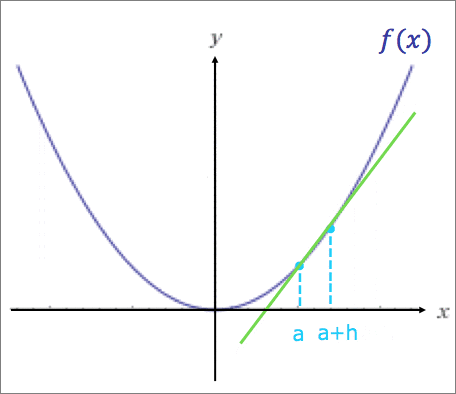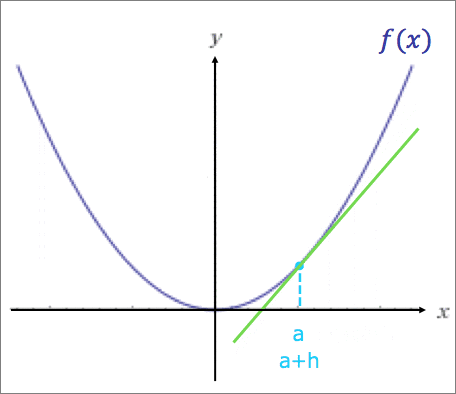
イメージ:
関数f(x)のx=aの点とx=a+hの点を結ぶ直線の、x+hをxに近づける(=hを0に近づける)
引用:【3分で分かる!】微分の計算のやり方・導関数の意味と求め方をわかりやすく
微分の公式
参考講義:https://youtu.be/SAZYMVGAiRM?si=YwanmZw4EfyhXElo
\begin{align}
y=f(x), \hspace{5pt} c:定数, \hspace{5pt} e:ネイピア数\\\\
y=c \hspace{10pt}→\hspace{10pt}f'(x) = \overbrace{(c)'}^{cの微分値という意味} = 0\hspace{5pt}\\
y=x \hspace{10pt}→\hspace{10pt}f'(x) = (x)'= x\hspace{5pt}\\
y=x^2 \hspace{5pt}→\hspace{5pt}f'(x) = (x^2)' = 2x\\
\end{align}
y=e^x \hspace{5pt}→\hspace{5pt}f'(x) = (e^x)' = e^x\\
y=e^{-x} \hspace{1pt}→\hspace{1pt}f'(x) = (-e^x)' = -e^x \\
※ネイピア数は微分しても値が変わらない
合成関数
合成関数とは、$ y=f(u), \ u=g(x) $のように、複数の関数の合成で表される関数のこと。
連鎖率
微分を分数で表現したものは以下のようにあらわすことができる。
合成関数を微分するときはこれを使う。
\frac{dy}{dx} = \frac{dy}{du}\frac{du}{dx}
シグモイド関数
yが0から1の間に収まる
シグモイド曲線は、こんな感じにS字のグラフになる

それを微分すると山なりのグラフになる(微分するときに合成関数を使う)
使われどころ:
勾配降下法、誤差逆伝播法でパラメーターの更新に使う
多変数関数と偏微分
$ y=f(x) $ x:独立変数、y:従属変数
$ y=f(x,y) $ 独立変数が2つ以上 ⇒多変数関数
使いどころ:
損失関数、誤差関数
勾配降下法→底のほう(小さいほう)に進むにはどうすればよいか計算する
偏微分
多変数関数を微分するときに、1つの変数にだけを変動させて、それ以外は定数として扱うこと
ベクトルといわれても、べの字もイメージできないところから、少しだけ理解するための記事です。
救世主:このサイトさえ見ればイメージは持てると思う
ベクトルとは?
- 「向き」と「大きさ」を持った量のこと
└矢印を思い浮かべるといいかも - 数のまとまりのこと(プログラムで言うところの配列)
\pmatrix{3}
\pmatrix{5\\3}
\pmatrix{3\\2\\2} \\
線形代数とは
ベクトル空間で様々な分析を行うこと
なぜ機械学習にベクトル・線形代数が必要か
大量のデータを扱うために、多次元行列(テンソル)を使うことが多い
これを使うことで、プログラムがシンプル&高速にできる
また、平面の向きを求めたり、距離を計算することにベクトルが使われている
使いどころ:文章の類似度(word2vec) など
ベクトルの計算方法
- ベクトルの足し算(成分の形や量が一致していなければ和は計算できない)
\pmatrix{2\\3}+\pmatrix{5\\3}=\pmatrix{7\\6}\
- ベクトルにマイナスをつけると、ベクトルの方向が逆になる
- ベクトルの倍率変更
ベクトルにベクトルでない数をかけると倍率変更ができる(この2とか-2とかのことをスカラーという)
2\pmatrix{2\\3} = \pmatrix{4\\6}\\
-2\pmatrix{2\\-3} = \pmatrix{-4\\6}
- ベクトルの大きさ
\sqrt{x^2+y^2} = \begin{Vmatrix} \pmatrix{x\\y} \end{Vmatrix}
- 矢印で表せるベクトルを幾何ベクトルという
次のベクトルは1次元,2次元,3次元を表すことができる
\pmatrix{3}
\pmatrix{5\\3}
\pmatrix{3\\2\\2}
…しかし次のようなベクトルもある
\pmatrix{3\\2\\2\\4}
\pmatrix{3\\2\\2\\1\\5}
数ベクトル
改めて、ベクトルの定義:
単数または複数の数字をひとまとめにしたもの
(本質的には複数の数字を扱う学問であって、複数の数字を扱うことで方向や大きさを見出すことができた)
\pmatrix{3\\2\\2\\\vdots\\n} ≠ (3,2,2,…,n)
- n次の列ベクトルとn次の行ベクトルは基本的には別物
- 行と列を入れ替えることができる=転置(左上にtをつける)
\pmatrix{3\\2\\2\\\vdots\\n} = ^t(3,2,2,…,n)
ベクトル空間
概念:
- ベクトルの集まり
- ベクトルの法則が成り立つ
補足:
- 軽量ベクトル空間:ベクトル+長さや角度等の概念(内積)
- 数学における空間:集合と演算ルールのこと
- 力を➡で書いたりするのもベクトル。大きさはあれど、長さはない。
基底
一次独立
- 平面上にあるすべてのベクトルは、その平面にあるベクトルのうち、最低2つでも表現できる
引用元:【ゆっくり解説】数学の見え方が変わる 「抽象と具体のベクトル数学 (線形代数)」【Voiceroid解説】
- 二つのベクトルよりも短いベクトルでも分数のスカラーを用いれば表現できる
- 一時独立にあるベクトルの組は**"基底(base)"**と呼ばれる
- ベクトル空間内の規定と呼べる組の数のことを**"次元(dimension)"**
→基底の数n個のベクトル空間 = n次元のベクトル空間
dim V = n n次元\\
dim V = 2 2次元
標準基底
ベクトルの成分に1つだけ'1'を含み、それ以外の成分はすべて'0'の基底
軽量ベクトル空間で考えると、角度は90度で直行しており、ノルム(大きさ)が1の単位ベクトルになる
\boldsymbol{e}_1=\pmatrix{1\\0\\0\\\vdots\\0},
\boldsymbol{e}_2=\pmatrix{0\\1\\0\\\vdots\\0} ,
\boldsymbol{e}_3=\pmatrix{0\\0\\1\\\vdots\\0} ,
\boldsymbol{e}_n=\pmatrix{0\\0\\0\\\vdots\\1} ,
ノルム

L1ノルム(マンハッタン距離): $ 3+4=7 $
L2ノルム(ユークリッド距離): $ \sqrt{3^2 + 4^2} = \sqrt{25} = 5 $
使いどころ:過学習を調整するときなど
一時従属
- こういうのだと二つあっても平面を表現することはできない
内積
成分同士のかけ算の総和で、内積は求められる。
例:
\begin{align}
a=(4,2), b=(3,6)\\
<a,b> = 4 \times 3 +2\times6\\
=24
\end{align}
図形的な求め方だと次のようになる
\boldsymbol{A・B} = \begin{Vmatrix} \boldsymbol{A}||\boldsymbol{B}\end{Vmatrix} cosθ\\
θ:角度
cos:θの値によって1~-1の間で変化する関数
AとBはノルムで、内積の値はスカラーになる
コサイン類似度
この図形的な求め方で何ができるかというと、角度を求めることができる!
→ベクトルの特性が似てるかどうかがわかるようになる
\begin{align}
\begin{Vmatrix} \boldsymbol{A}\end{Vmatrix}\begin{Vmatrix} \boldsymbol{B}\end{Vmatrix} cosθ
= \pmatrix{a' b' c'} \pmatrix{a\\b\\c}\\=aa' +bb' + cc'
\end{align}
使いどころ:自然言語処理(word2vecなど)
(二つの値のベクトルを計算して、その値が大きければ二つのベクトルの値が類似。小さければ特徴が離れていることを示している)
法線ベクトル
三次元の球体に接している平面は一点で接している。
接平面を決めるためには、その平面に垂直なベクトルがわかればよい。
この平面と直行しているベクトルのことを法線ベクトルという

行列
加算・減算
ベクトルの計算と同じ感じ
\pmatrix{2&1\\3&5}+\pmatrix{5&1\\3&7}=\pmatrix{7&2\\6&12}\
乗算
\pmatrix{1& 2 & 3} \pmatrix{4\\5\\6}=1\times4+2\times5+3\times6
例:1行3列 3行1列
上記のように最小の行列の列数と二番目の行列の行数が一致していることがかけ算ができることの条件
逆行列
行列計算に割り算はない→逆数に相当する計算はある
x\div\frac{3}{5}=x\times\underbrace{\frac{5}{3}}_{逆数}\\
\pmatrix{a&b\\c&d} の逆行列は\frac{1}{ad-bc}\pmatrix{d&-b\\-c&a}