こんにちは。前回Hemispherical Harmonic Interpolationを用いたRadiance Caching(その1)で説明した話の続きです。HSH係数を回転させることで、座標系を揃えて内挿します。
目次
1.はじめに
2.回転行列の分解
3.z軸周りの回転
4.y軸周りの回転
5.半球面調和展開係数の補間
[6.Out-going Radiance](#6-Out-going Radiance)
7.最後に
8.参考文献
1.はじめに
[GKPB04]ではHSH係数の回転は[IR96]と[IR98]を参考にしたという話をしています。しかし、[IR96]は非常に複雑であり、計算量が非常に多いので、[KKPB05]で現実的な時間で計算できるように回転行列$R$を2次の成分までテイラー展開するという手法が考案されました。今回はその手法を紹介します。流れは$R$をZYZ回転(ローカル)用に分解($\alpha,\beta,\gamma$)してSHS係数を回転させるだけなのだが、イメージが難しい部分や計算が複雑な部分がある。
これが出来ると、HSH係数に重みをかけて足し合わせることで、対象にしている点でのOut-going Radianceが求められる。
2.回転行列の分解
このセクションの目標は下図のような二つの座標系をローカルな座標系で見てZYZ回転をすることで座標系を揃えることである。言葉ばかりでは伝わらないので、数式を交えながら説明する。

座標系$n$は$n_x,n_y,n_z~(|n_x|=|n_y|=|n_z|=1)$を基底ベクトルとする三つのベクトルから成る。(今後基底ベクトルはすべて大きさ1とする。)これら3つのベクトルを以下の手順で回転させる。
➀$n_z$を軸として、$\alpha$だけ回転させる。新たな座標系$n^1$は$n^1_x,n^1_y,n^1_z$から成る。この時、$n^1_z = n_z$である。
➁$n^1_y$を軸として、$\beta$だけ回転させる。新たな座標系$n^2$は$n^2_x,n^2_y,n^2_z$から成る。この時、$n^2_y = n^1_y$である。
➂$n^2_z$を軸として、$\gamma$だけ回転させる。新たな座標系$n^3$は座標系$n^g$と一致し、$n^g_x,n^g_y,n^g_z$から成る。この時、$n^g_z = n^g_z$である。
このことを整理して、$\alpha,\beta,\gamma$を求めることになる。最も重要なのは、z軸
は➁のタイミングで一度しか変換されないということである。この時の回転角$\beta$は$n_z$と$n^g_z$の間の角であると言える。このことを考えると➀の操作で$n^1_y$は$n_z$と$n^g_z$がなす平面と垂直でなければならない。
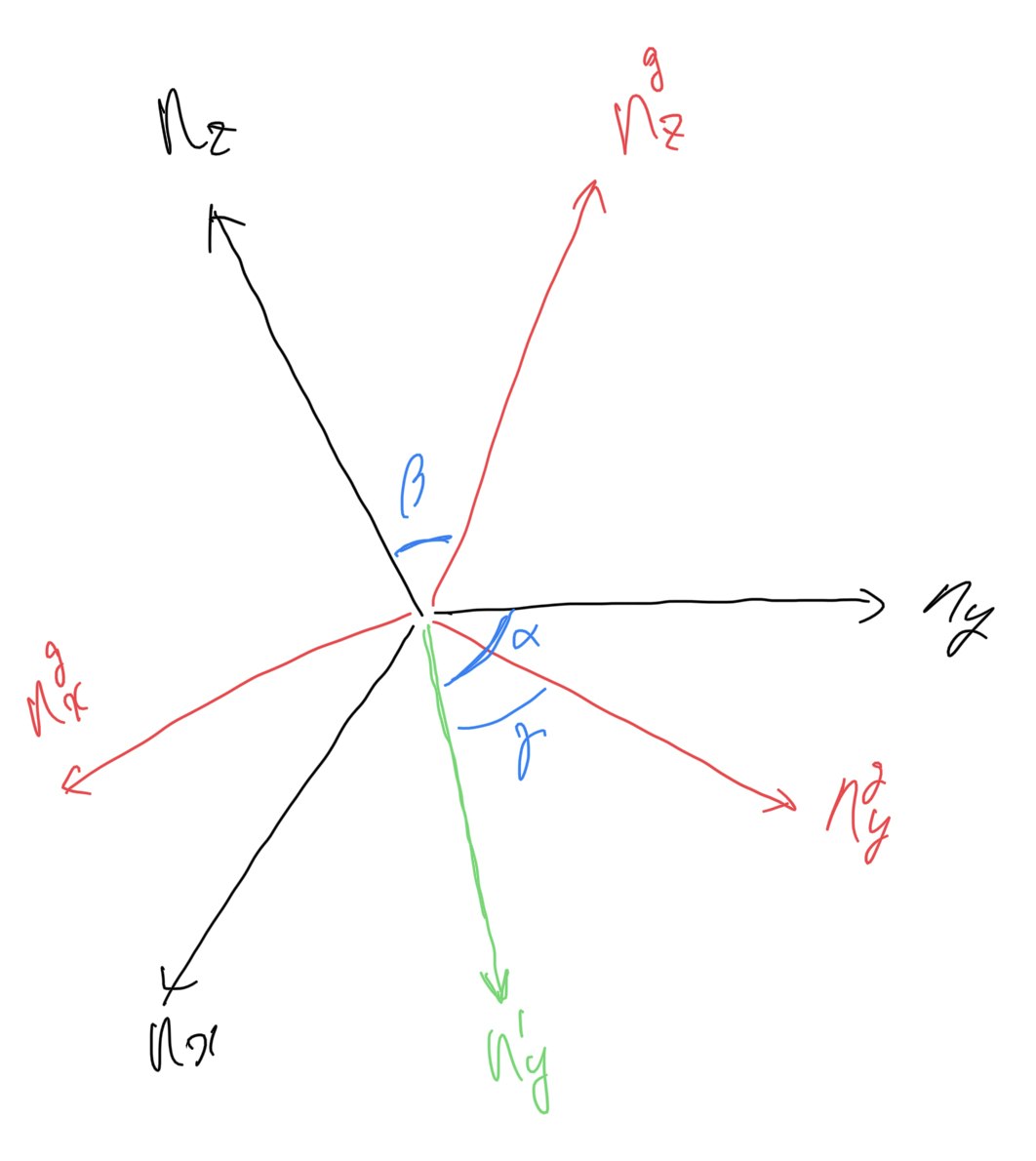
以上の考察から、$\alpha,\beta,\gamma$は以下のように書ける。
\cos \alpha = \frac{n_z \times n^g_z}{ |n_z \times n^g_z|}\cdot n_y \tag{H24}
\cos \beta = n_z \cdot n^g_z \tag{H25}
\cos \gamma = n^1_y \cdot n^g_y \tag{H26}
ここで、$n^1_y$だけは与えられていないので、計算で求める必要がある。これは、$n_z$を軸としてロドリゲスの回転公式を用いて、$n_y=(n_{y1},n_{y2},n_{y3})$を$\alpha$分回転させることで得られる。
n^1_y = R_Z(\theta) n_y \tag{H27}
R_Z(\theta) =
\begin{pmatrix}
n^2_{y1}(1-\cos\theta) + \cos \theta & n_{y1}n_{y2}(1-\cos\theta) - n_{y3} \sin \theta & n_{y1}n_{y3}(1-\cos\theta) + n_{y2} \sin \theta\\
n_{y1}n_{y3}(1-\cos\theta) + n_{y3} \sin \theta & n^2_{y2}(1-\cos\theta) + \cos \theta & n_{y2}n_{y3}(1-\cos\theta) - n_{y1} \sin \theta\\
n_{y1}n_{y3}(1-\cos\theta) - n_{y2} \sin \theta & n_{y2}n_{y3}(1-\cos\theta) + n_{y1} \sin \theta & n^2_{y3}(1-\cos\theta) + \cos\theta
\end{pmatrix} \tag{H28}
ここまでの話を用いて$R$を分解することで、以下のようになる。
R(\theta) \Lambda = R_Z(\gamma)R_Y(\beta)R_Z(\alpha)\Lambda \tag{H29}
3.z軸周りの回転
z軸周りの回転は比較的簡単にできる。東西波数mに従って、以下のような変換を行うことで、$\Lambda^1 = R_Z(\alpha)\Lambda$が得られる。
\lambda^1_{nm} =
\begin{cases}
\lambda_{n0}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(m=0)\\
\lambda_{n,-m}\sin(m\alpha) + \lambda_{nm} \cos(m\alpha)~~~~~~~~(m \neq 0) \tag{H30}
\end{cases}
この計算は➃の$\gamma$だけ回転させる過程でも使える。
4.y軸周りの回転
y軸周りの回転は以下のような二次のテイラー展開を用いる。
R_Y(\beta) = I + \beta \frac{dR_Y}{d\beta}(0) + \frac{\beta^2}{2} \frac{d^2R_Y}{d\beta^2}(0) \tag{H31}
\frac{dR_Y}{d\beta}(0) =
\begin{pmatrix}
0 & \mathbf{0} & \mathbf{0} & \mathbf{0} & \cdots \\
\mathbf{0} & \frac{dR^1_Y}{d\beta}(0) & \mathbf{0}& \mathbf{0}& \cdots\\
\mathbf{0} & \mathbf{0} & \frac{dR^2_Y}{d\beta}(0)& \mathbf{0}& \cdots\\
\mathbf{0} & \mathbf{0} & \mathbf{0} &\frac{dR^3_Y}{d\beta}(0)& \cdots\\
\vdots & \vdots & \vdots & \vdots & \ddots
\end{pmatrix}\tag{H32}
\frac{d^2R_Y}{d\beta^2}(0) =
\begin{pmatrix}
0 & \mathbf{0} & \mathbf{0} & \mathbf{0} & \cdots \\
\mathbf{0} & \frac{d^2R^1_Y}{d\beta^2}(0) & \mathbf{0}& \mathbf{0}& \cdots\\
\mathbf{0} & \mathbf{0} & \frac{d^2R^2_Y}{d\beta^2}(0)& \mathbf{0}& \cdots\\
\mathbf{0} & \mathbf{0} & \mathbf{0} &\frac{d^2R^3_Y}{d\beta^2}(0)& \cdots\\
\vdots & \vdots & \vdots & \vdots & \ddots
\end{pmatrix}\tag{H33}
$\frac{dR^{(k)}_Y}{d\beta}(0)$と$\frac{d^2R^{(k)}_Y}{d\beta^2}(0)$は(2k+1)×(2k+1)のサイズの正方行列であり、各成分は以下の数式群から求められる。今後は$\frac{d^kR^{(l)}_Y}{d\beta^k}(0)$を$R^{(k)}_Y(l,m_1,m_2)$と表記する。$l=0,1$については以下の通りである。(k,l,m,nなどの文字に注意。入れ替えが発生)
R^{(k)}_Y(0,0,0) = 1^{(k)} \\
R^{(k)}_Y(1,-1,-1) = 1^{(k)} ~,~R^{(k)}_Y(1,-1,0) = 0~,~R^{(k)}_Y(1,-1,1) = 0 \\
R^{(k)}_Y(1,0,-1) = 0 ~,~R^{(k)}_Y(1,0,0) =\cos^{(k)}(\beta) ~,~R^{(k)}_Y(1,0,1) = -\sin^{(k)}(\beta) \\
R^{(k)}_Y(1,1,-1) = 0 ~,~R^{(k)}_Y(1,0,0) =\sin^{(k)}(\beta) ~,~R^{(k)}_Y(1,0,1) = \cos^{(k)}(\beta) \\
$1^{(k)}$は$k=0$の時1で$ k \neq 0$の時0になる。
k=1、l=1について行列の形で書き直すと、
\frac{d^kR^{(1)}_Y}{d\beta^k}(0) =
\begin{pmatrix}
0 & 0 & 0\\
0 & -\sin \beta & - \cos \beta\\
0 & \cos \beta & \sin \beta \\
\end{pmatrix} \tag{H34}
このことと以下の式からH33とH34の成分が計算できる。
R^{(k)}(l,m_1,m_2) = u^l_{m1m2} \cdot dU^{(k)}(l,m1,m2) + v^l_{m1m2} \cdot dV^{(k)}(l,m1,m2)\\ + w^l_{m1m2} \cdot dW^{(k)}(l,m1,m2) \tag{H35}
u^l_{m_1m_2} =
\begin{cases}
\bigg[ \frac{(l+m_1)(l-m_1)}{(l+m_2)(l-m_2)} \bigg]^{\frac{1}{2}} ~~~~~~~~~~~~(|m_2| < l)\\
\bigg[ \frac{(l+m_1)(l-m_1)}{(2l)(2l-1)} \bigg]^{\frac{1}{2}}~~~~~~~~~~~~(|m_2| = l)
\end{cases} \tag{H36}
v^l_{m_1m_2} =
\begin{cases}
\frac{1}{2}\bigg[ \frac{(l+\delta_{m_10})(l+|m|-1)(l+|m_1|)}{(l+m_2)(l-m_2)} \bigg]^{\frac{1}{2}}(l-2\delta_{m_10}) ~~~~~~~~~~~~(|m_2| < l)\\
\frac{1}{2}\bigg[ \frac{(l+\delta_{m_10})(l+|m|-1)(l+|m_1|)}{(2l)(2l-1)} \bigg]^{\frac{1}{2}}(l-2\delta_{m_10}) ~~~~~~~~~~~~(|m_2| = l)\\
\end{cases} \tag{H37}
w^l_{m_1m_2} =
\begin{cases}
-\frac{1}{2}\bigg[ \frac{(l-|m_1|-1)(l-|m_1|)}{(l+m_2)(l-m_2)} \bigg]^{\frac{1}{2}}(l-\delta_{m_10}) ~~~~~~~~~~~~(|m_2| < l)\\
-\frac{1}{2}\bigg[ \frac{(l-|m_1|-1)(l+|m_1|)}{(2l)(2l-1)} \bigg]^{\frac{1}{2}}(l-\delta_{m_10}) ~~~~~~~~~~~~(|m_2| = l)\\
\end{cases} \tag{H38}
dU^{(k)}(l,m1,m2) = dP^{(k)}(l,m_1,m_2,0) \tag{H39}
dV^{(k)}(l,m1,m2) =
\begin{cases}
dP^{(k)}(l,m_1-1,m_2,1)-dP^{(k)}(l,-m_1+1,m_2,-1) ~~~~~(m_1>1)\\
\sqrt{2}dP^{(k)}(l,0,m_2,1) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(m_1=1)\\
dP^{(k)}(l,1,m_2,1) + dP^{(k)}(l,-1,m_2,-1) ~~~~~~~~~~~~~~~~~~~~~~~~~(m_1 = 0)\\
\sqrt{2}dP^{(k)}(l,0,m_2,-1) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(m_1=-1)\\
dP^{(k)}(l,m_1-1,m_2,-1)+dP^{(k)}(l,-m_1+1,m_2,1) ~~~~~(m_1<-1)
\end{cases}\tag{H40}
dW^{(k)}(l,m1,m2) =
\begin{cases}
dP^{(k)}(l,m_1+1,m_2,1)+dP^{(k)}(l,-m_1-1,m_2,-1) ~~~~~(m_1>0)\\
dP^{(k)}(l,m_1-1,m_2,1)-dP^{(k)}(l,-m_1+1,m_2,-1) ~~~~~(m_1 \leq 0)
\end{cases}\tag{H41}
dP^{(k)}(l,m1,m2,i) =
\begin{cases}
dT^{(k)}(1,i,0,l-1,m_1,m_2) ~~~~~~~~~~~~~~~~~~~~~~~(|m_2|<l)\\
dT^{(k)}(1,i,1,l-1,m_1,l-1)\\-dT^{(k)}(1,i,-1,l-1,m_1,-l+1) ~~~~~(m_2=l)\\
dT^{(k)}(1,i,1,l-1,m_1,-l+1)\\+dT^{(k)}(1,i,-1,l-1,m_1,l-1) ~~~~~(m_2=-l)
\end{cases}\tag{H42}
dT^{(k)}(l,m_1,m_2,l',m'_1,m'_2) = \sum^k_i {}_n C_k R^{(k)}(l,m_1,m_2) R^{(k-i)}(l',m'_1,m'_2) \tag{H43}
以上の式を利用すれば、$R_Y(\beta)を計算できる。
5.半球面調和展開係数の補間
ここまでのことを用いれば、In-coming Radianceを利用して、Out-going Radianceを求めようとする点$p$について、近傍のHSH係数から$p$でのIn-coming RadianceのHSH係数を補間できる。以下がそれを計算するための式である。
\Lambda(p) = \frac{\sum^S_{i} R_i(\Lambda_i + d_x\frac{\partial \Lambda_i}{\partial x} + d_y\frac{\partial \Lambda_i}{\partial y})w_i(p)}{\sum^S_{i} w_i(p)} \tag{H44}
Sは近傍のHSH係数保存点の数を表し、$R_i$は回転行列を表す。
6.Out-going Radiance
Out-going Radianceは本来であれば、以下のような輸送方程式を用いて計算されます。
L_o(p) = \int_{\Omega} f(\omega_i,\omega_o) L_i(p) (n\cdot \omega_i) d\omega_i \tag{H45}
しかし、In-coming RadianceとBRDFがHSH係数の場合は、以下のように簡単な形に書き換えることができる。
L_o(p) = \sum^{n-1}_{l=0} \sum^{l}_{m=-l} \lambda_{lm} f_{lm}(\theta_o,\phi_o) \tag{H46}
7.最後に
以上で、Hemispherical Harmonic Interpolationを用いたRadiance Cachingのアルゴリズムを全て説明した。
8.参考文献
[GKPB04]
Pascal Gautron, Jaroslav Kˇrivánek, Sumanta N. Pattanaik, and Kadi Bouatouch. A novel hemispherical basis for accurate and efficient rendering. In Eurographics Symposium on Rendering (to appear), June 2004.
[KGPB05]
Jaroslav Kˇrivánek, Pascal Gautron,Sumanta N. Pattanaik, and Kadi Bouatouch 2005. Radiance caching for efficient global illumination computation. Transactions on Visualization and Computer Graphics
[KKPB05]
Jaroslav Krivánek, Jaakko Konttinen, Sumanta Pattanaik, Kadi Bouatouch. Fast Approximation to Spherical Harmonic Rotation. [Research Report] PI 1728, 2005, pp.14.
[IR96]
IVANIC J., RUEDENBERG K.: Rotation matrices for real spherical harmonics. direct determination by recursion. J. Phys. Chem. 100, 15 (1996), 6342–6347
[IR98]
Joseph Ivanic and Klaus Ruedenberg. Additions and corrections : Rotation matrices for real spherical harmonics. J. Phys. Chem. A, 102(45):9099–9100, 1998.