はじめに
"Pythonではじめる機械学習"の決定木のアンサンブル法(p82~90)の学習記録です。
・分からなかったコードやドキュメント
・自分にとって理解するのに時間がかかった内容
・用語の定義
に関する説明を主に記述しています。
参考書を読んでいて容易に理解できたことは記述していません。
2.3.7 カーネル法を用いたサポートベクタマシン
2.3.7.1 線形モデルと非線形特徴量
低次元における線形モデルは非常に制約が強いので、線形モデルを柔軟にするために特徴量を加える。
# In[76]
2番目の特徴量の2乗を追加。
# np.hstackで横方向に配列を連結する(feature0, feature1)が(feature0, feature1, feature1 ** 2)となる
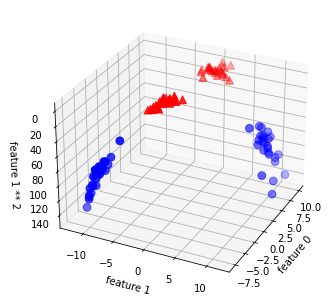
X_new = np.hstack([X, X[:, 1:] ** 2])
# 3Dで可視化する
from mpl_toolkits.mplot3d import Axes3D, axes3d
figure = plt.figure()
# elevはz方向から見た仰角、azimはx,y軸方向の方位角を指定
ax = Axes3D(figure, elev=-152, azim=-26)
# y== 0の点をプロットしてからy == 1の点をプロット
mask = y == 0
# 青点の設定
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b', cmap=mglearn.cm2, s=60)
# 赤点の設定
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^', cmap=mglearn.cm2, s=60)
ax.set_xlabel("feature 0")
ax.set_ylabel("feature 1")
ax.set_zlabel("feature 1 ** 2")
疑問
・maskって何?
# In[77]
# ravelで多次元のリストを一次元として返す
linear_svm_3d = LinearSVC().fit(X_new, y)
coef, intercept = linear_svm_3d.coef_.ravel(), linear_svm_3d.intercept_
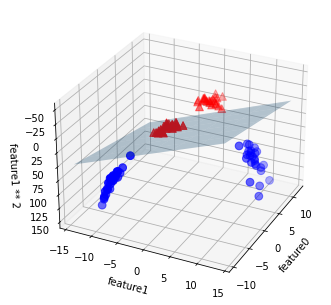
# 線形決定境界を描画
figure = plt.figure()
ax = Axes3D(figure, elev=-152, azim=-26)
xx = np.linspace(X_new[:, 0].min() - 2, X_new[:, 0].max() + 2, 50)
yy = np.linspace(X_new[:, 1].min() - 2, X_new[:, 1].max() + 2, 50)
# xx, yyの各座標の要素列から格子座標を作成する
XX, YY = np.meshgrid(xx, yy)
ZZ = (coef[0] * XX ++ coef[1] * YY + intercept) / -coef[2]
ax.plot_surface(XX, YY, ZZ, rstride=8, cstride=8, alpha=0.3)
# 青点の作成
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b', cmap=mglearn.cm2, s=60)
# 赤点の作成
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^', cmap=mglearn.cm2, s=60)
ax.set_xlabel("feature0")
ax.set_ylabel("feature1")
ax.set_zlabel("feature1 ** 2")
疑問
・linspace(数列作成)の引数
・plot_surfaceの引数
# In[78]
ZZ = YY **2
# 横方向に配列を連携する(np.hstackと同じ)
dec = linear_svm_3d.decision_function(np.c_[XX.ravel(), YY.ravel(), ZZ.ravel()])
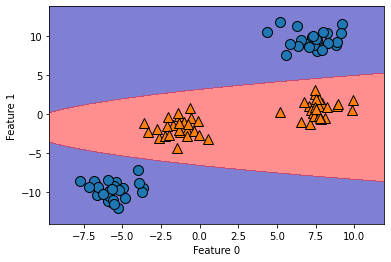
# plt.contourfで塗りつぶした等高線を描画する
plt.contourf(XX, YY, dec.reshape(XX.shape), levels=[dec.min(), 0, dec.max()], cmap=mglearn.cm2, alpha=0.5)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
2.3.7.2 カーネルトリック
以上から、非線形の特徴量をデータ表現に加えることで、線形モデルがはるかに強力になるということが分かる。
非常に大きくなりうる表現(たくさんの特徴量など)を実際に計算せずに、高次元空間でのクラス分類器を学習させる巧妙な数学的トリックがカーネルトリックである。
サポートベクタマシンで広く用いられている高次元空間へのマップ方法
・もとの特徴量の特定の次数までのすべての多項式を計算する多項式カーネル
・放射基底関数と呼ばれるガウシアンカーネル
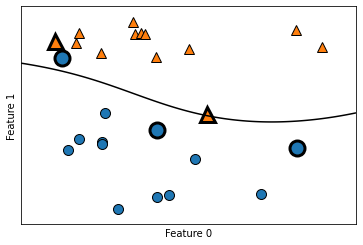
SVMを理解する
SVMでは2つのクラスの決定境界に位置するごく一部の訓練データポイント(多くの場合、これらのデータポイントが決定境界を決定する)をサポートベクタと呼ぶ。
# In[79]
from sklearn.svm import SVC
X, y = mglearn.tools.make_handcrafted_dataset()
svm = SVC(kernel='rbf', C=10, gamma=0.1).fit(X, y)
mglearn.plots.plot_2d_separator(svm, X, eps=.5)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
# サポートベクタをプロットする
sv = svm.support_vectors_
# サポートベクタのクラスラベルはdual_coef_の正負によって決まる
sv_labels = svm.dual_coef_.ravel() > 0
mglearn.discrete_scatter(sv[:, 0], sv[:, 1], sv_labels, s=15, markeredgewidth=3)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
疑問
・SVCと2dとscatterの引数
2.3.7.5 SVMのためのデータ前処理
In[86]の出力が参考書と何故か違う