数列の総和をダブリングで算出する。
具体的な処理のイメージを湧かせるのが目的なのでコードは出てこない。
ダブリングで総和を求める
例えば、次のような公比2の等比数列があったとする。
等比数列などでは公式により算出可能だがここではあえて利用しない。
1 \quad 2 \quad 4 \quad 8 \quad ・・・
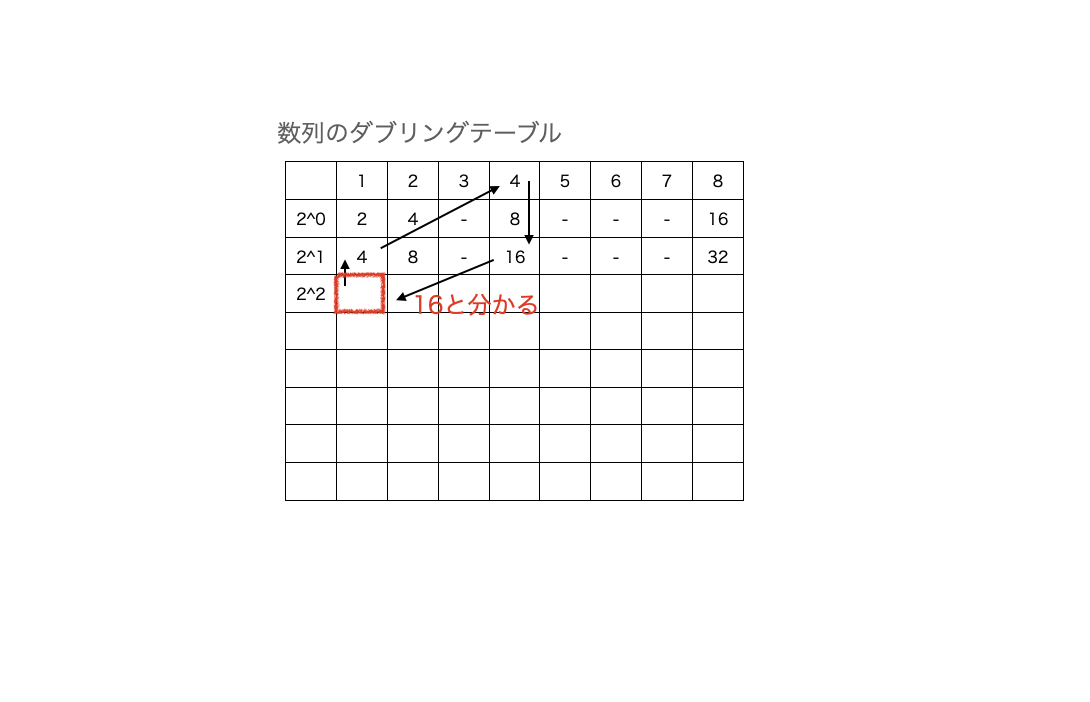
この数列のk項目(kはだいたい10^18とか膨大)を求める場合、ダブリングにより以下のようなテーブルを作成することで算出することができる。
例えば第5項目(=4回の公比を掛ける操作後時点)を求めるには以下。
表の縦軸は公比を掛ける回数(2^n)、横軸は掛けられる数である。
この辺は昔の記事にまとめた。
では和を求める場合はどうするか?
1 + 2 + 4 + 8 + ・・・
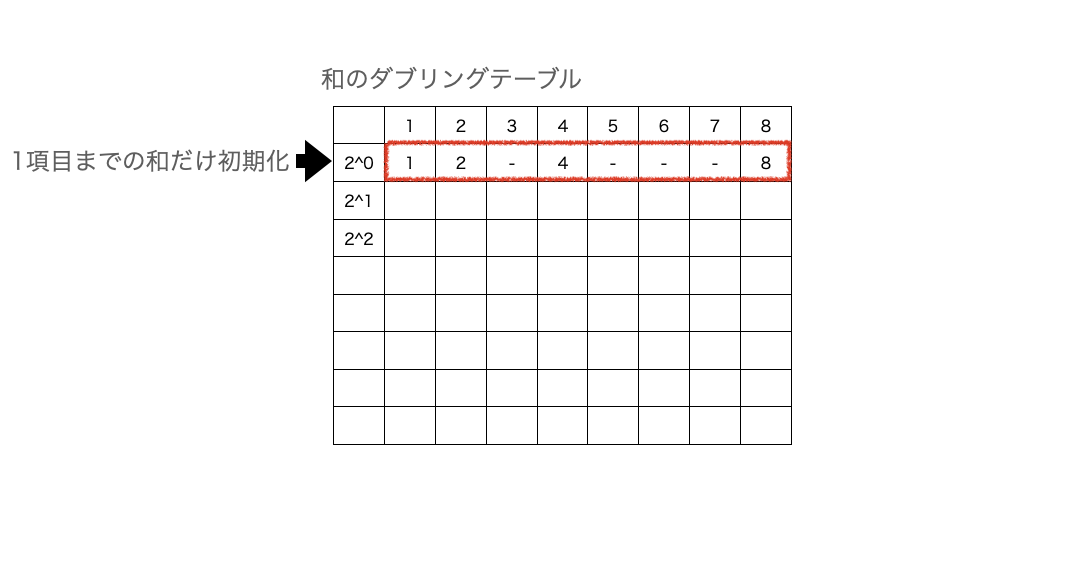
この場合、新たに和のダブリングテーブルを用意し、以下の容量で表を埋めていく。
例えば第4項までの和を求める方法は以下。
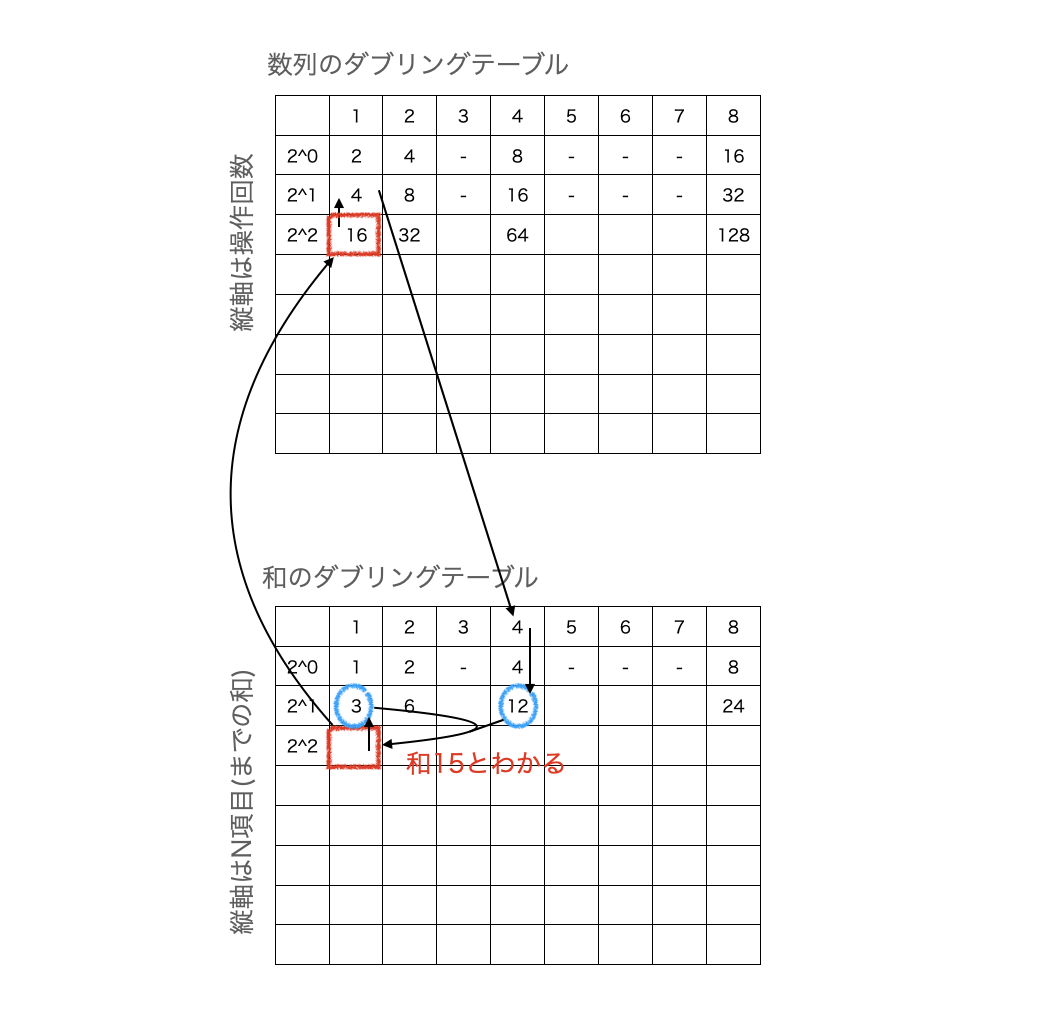
これは何をしているかというと、
N項目までの和 = [1項目からN/2項目までの和] + [N/2+1項目からN項目までの和]
であることから、
初項を開始状態とした和のダブリングテーブルの2^1項目までの和とN/2+1項目を開始状態としたダブリングの2^1項目までの和の総和を求めている。
絵にすると以下。
そのため、一度、N/2+1項目の数を求めるために数列のダブリングテーブルを参照している。
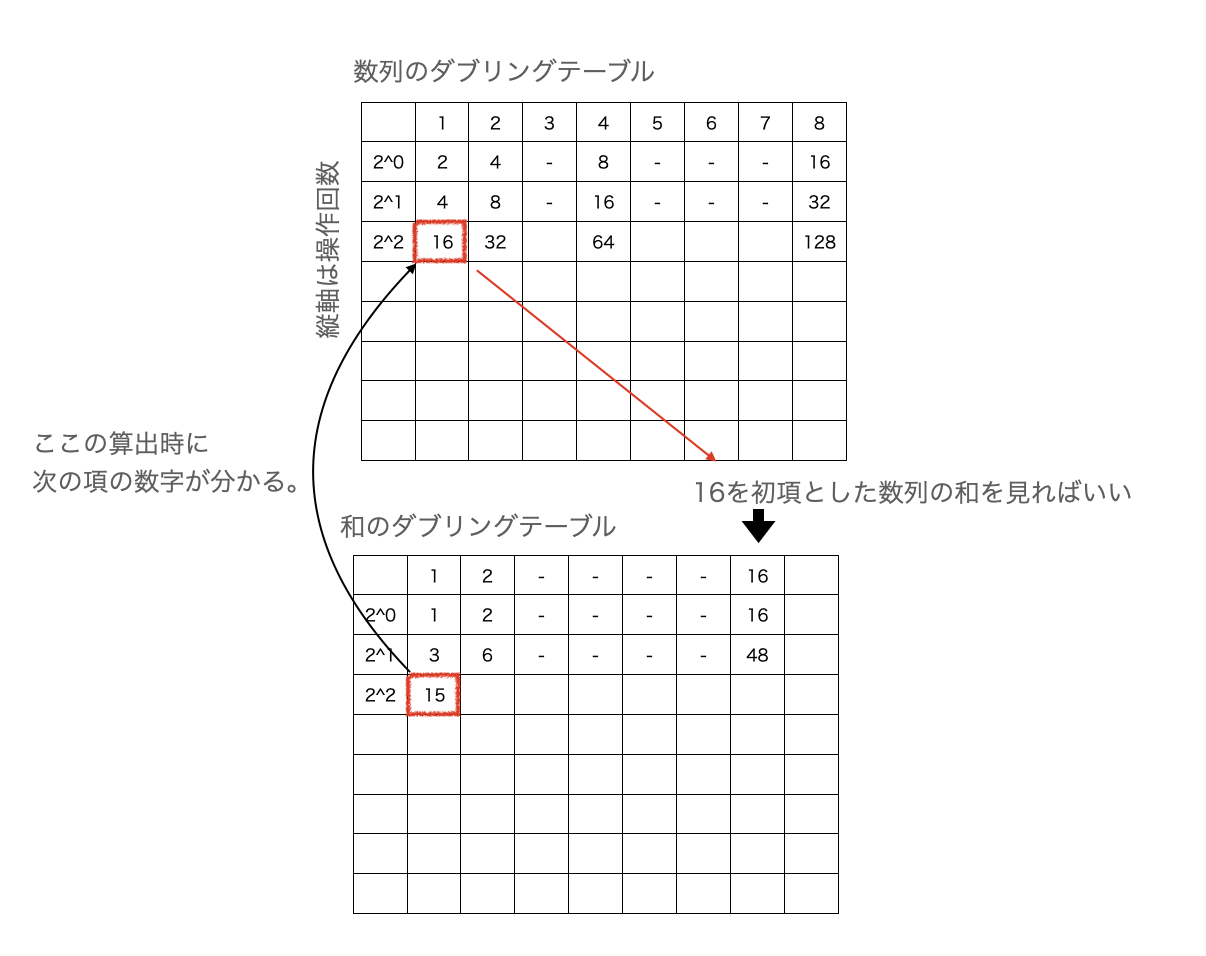
では中途半端な項までの和を求めるにはどうするか?
例えば第5項までの和では以下のように表現できる。
5 = 2^2 + 2^0
であることから、2^2項目までの総和を求め、まだ足していない第5項の数を数列のダブリングテーブルから算出する。
この第5項目を新たな初項として2^0項目までの数列と見なすことで、先ほど構築した和のダブリングテーブルを再利用することができ、その和が16と読み取れる。よって、15 + 16で算出できる。
1 + 2 + 4 + 8 + 16 + 32 ・・・
同じく、第6項目までの和が知りたいのなら以下であることから、15 + 48で算出できる。
5 = 2^2 + 2^1
この操作を繰り返すことで、膨大な第N項までの和を要求されても処理することができる。
等比数列などでは値が無限に大きくなるのでなんとも言えないが、modとった特殊な数列などでは出現する数(テーブルの横軸)に上限(Mとする)があるので、求めたい第N項までのテーブル構築にO(MlogN)。総和の算出にO(logN)。よってO(MlogN)で算出できる。
例題
余談
ただ、modとった数列の場合どこかで同じ数字が出現するとそれ以降は同じ流れの繰り返しになる(鳩の巣)ので、周期性を使って1発で計算することもできるので、必要ないと言えば必要ない。