いつ使うのか

同じ操作を繰り返したN回目の状態を求める時。
(特に、一つの局面に複数の要素があり、互いに遷移する場合に有効)

何がいいのか

通常、端からするとO(N)のオーダーがかかるところをO(logN)に短縮することができる。
繰り返し二乗法もこの一種。
上記のような複数の要素X個に対してN回操作した結果全てを求める場合にO(XlogN)に抑えられるのは大きい。

どうするのか

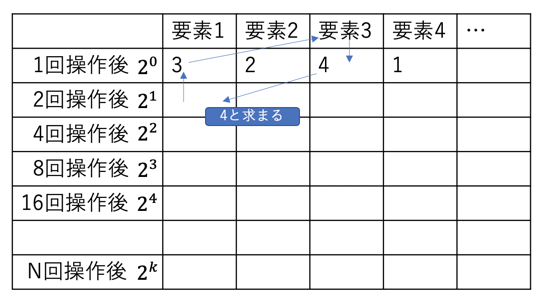
繰り返し二乗法と考え方は一緒。1回目の結果から2回目を、2回目の結果から4回目の結果を、、、と求めていく。
配列（複数の要素を同時に操作していく場合には二次元になる）に各操作後の状態をメモしていく(なんかdpみたい？)。

イメージ

考えること

N回目がちょうど2^kで表せれば直接リストを参照できるが、端数になる場合には構築した配列を元に繰り返し参照してN回目を出す。
eg) 5回目は4回目の結果を参照したのち1回目の結果を参照して出せる。
この過程ではビット演算が有力。

ビットに直した時に何ビット目が立っているか

a = []
for i in range(int(math.log2(K)) + 1):
    if K>>i & 1:
        a.append(i)

テンプレート

X個の要素のN回操作後を求める表を作る。

# 二次元配列作成
dv = []
for _ in range(int(math.log2(K)) + 1):
    l = [0] * X
    dv.append(l)

# dv[0][0:X]を初期化

# ダブリングで表を構築
for k in range(1, int(math.log2(K)) + 1):
    for n in range(N):
        dv[k][n] = dv[k - 1][dv[k - 1][n]]

使用例

繰り返し二乗法

MOD = 10 ** 9 + 7

def mod_pow(x: int, n: int):
    bi = str(format(n, "b"))
    res = 1
    a = x
    for i in range(len(bi)):
        if n >> i & 1:
            res = (res * a) % MOD
        a = (a * a) % MOD
    return res

ABC167 D - Teleporter

今回に関しては10^18 ≒ 2^60なので、60まで見れば良い。
log2(K) + 1を都度計算しても可。

def main():
    N, K = map(int, input().split())
    A = [int(i) for i in input().split()]

    dv = []
    for _ in range(60):
        l = [0] * N
        dv.append(l)

    for n in range(N):
        dv[0][n] = A[n] - 1

    for k in range(1, 60):
        for n in range(N):
            dv[k][n] = dv[k - 1][dv[k - 1][n]]

    a = []
    for i in range(60):
        if K>>i & 1:
            a.append(i)

    now = 0
    for i in a:
        now = dv[i][now]
    print(now + 1)

PythonだとTLEしたのでPyPyで。

ABC136 D - Gathering Children

10 ** 100(googol)回目を求めるのO(XlogN)でもきつい。
最終的にRLの間で行き来する状態を繰り返すだけになるので操作回数の偶奇だけを気にすればよい。
さらにSの右端以外全部Rみたいなケースだったとしても最大文字数10 ** 5回まわせば最終局面になることがわかる。

# log2(10 ** 5) ≒ 16.6 → 最終的にans[17][]が求まれば良い。
LOG = 18

def main():
    S = input()
    N = len(S)
    to = []
    for _ in range(LOG):
        l = [0] * N
        to.append(l)

    for i in range(N):
        to[0][i] = i + 1 if S[i] == "R" else i - 1

    for i in range(1, LOG):
        for j in range(N):
            to[i][j] = to[i - 1][to[i - 1][j]]

    ans = [0] * N
    for j in range(N):
        ans[to[LOG - 1][j]] += 1

    L = [str(i) for i in ans]
    print(" ".join(L))
    return

参考

ダブリングを利用して数列の総和を求める方法 (2021/08/10追記)

別記事で記述。

[競プロ用]ダブリングまとめ