日本のコロナ患者数データを解析する

日本のコロナ患者数データを解析して予測モデルを作っていきます。

ここでは
・Facebookが提供しているProphetというライブラリを使用する方法
・ランダムフォレスト回帰
・XGBoost
という３つの手法を試します。

環境

Windows10にAnacondaをインストールしたときに一緒にインストールされるJupyter Notebookを使用

バージョン情報：
Jupyter Notebook 6.1.4
Python 3.8.5

ライブラリのインポート

fbprophet、plotly、およびxgboostをそれぞれAnacona Promptで
　conda install -c conda-forge fbprophet
　pip install plotly
　pip install xgboost
でインストールした上で、JupyterNotebook上で以下によりライブラリのインポートを行った。

import pandas as pd
import seaborn as sns
import numpy as np
from scipy.stats import norm
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import StandardScaler
pd.pandas.set_option('display.max_columns', None)
from scipy import stats
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
from sklearn.linear_model import Lasso
from sklearn.feature_selection import SelectFromModel
pd.pandas.set_option('display.max_columns', None)
import matplotlib.pyplot as plt
from fbprophet import Prophet
import plotly.express as px
from sklearn.ensemble import RandomForestRegressor
from xgboost import XGBRegressor
from sklearn.metrics import accuracy_score
from sklearn import metrics
from sklearn.model_selection import ParameterGrid
from tqdm import tqdm
from sklearn.pipeline import Pipeline
from sklearn.decomposition import PCA

使用するデータ

• nhk_news_covid19_domestic_daily_data.csv：　NHKが発表しているコロナ患者数データ

データ提供元：
https://www3.nhk.or.jp/news/special/coronavirus/data-all/

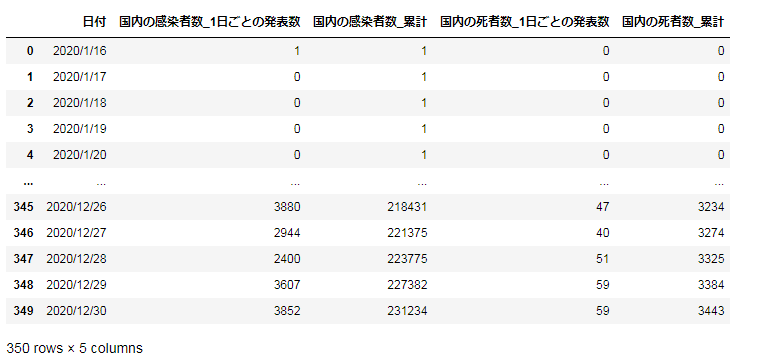
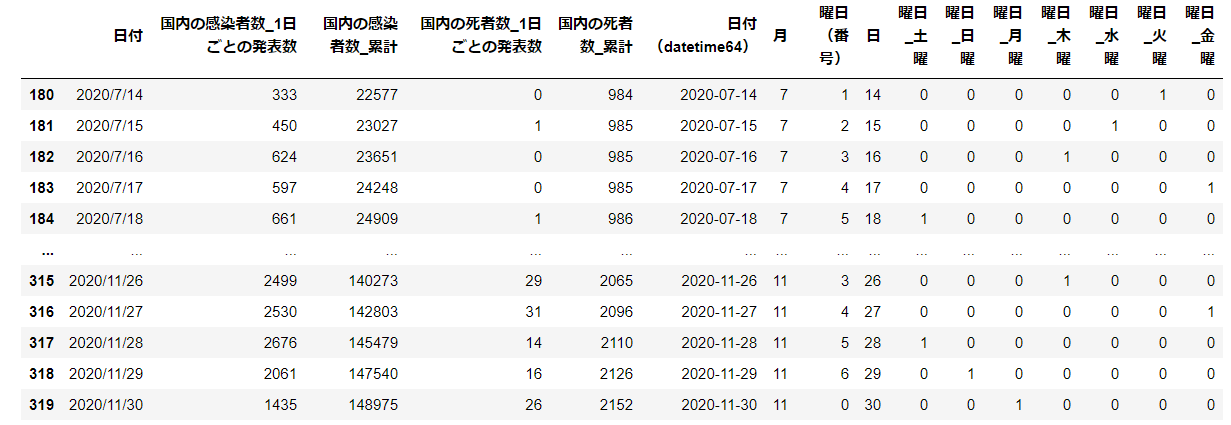
患者数データをデータフレームとして表示：

path = "../input/covid19data_from_NHK/nhk_news_covid19_domestic_daily_data.csv"
df_Jap = pd.read_csv(path,encoding = 'utf-8')
df_Jap

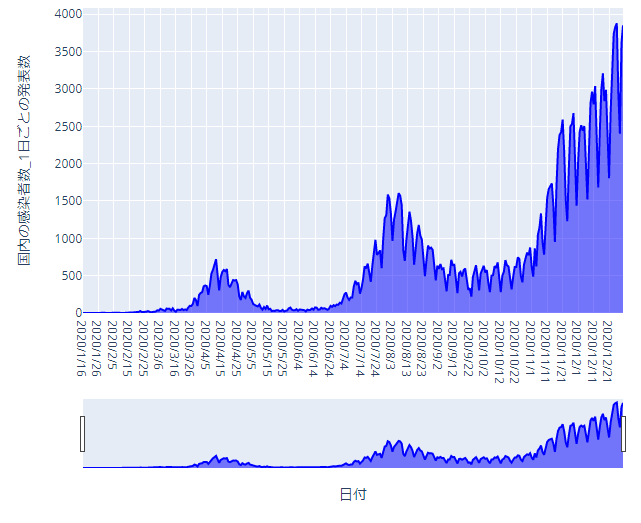
グラフの表示：

fig = px.area(df_Jap, x="日付", y="国内の感染者数_1日ごとの発表数", height=600, width=700,
             color_discrete_sequence = ["blue"])
fig.update_layout(xaxis_rangeslider_visible=True)
fig.show()

2020年の4月ごろ第一波、8月ごろ第二波、12月ごろ第三波が来ているのがわかります。

トレーニングデータとテストデータ

データをトレーニングデータとテストデータに分けるのですが、ここでは
トレーニングデータ：2020/7/14～2020/11/30
テストデータ：2020/12/1～2020/12/31
とします。
2020/7/14～としたのはそれ以前は患者数が0に近く、データの特徴が変わると考えたからです。

ここで「日付」列はpandasのto_datetimeメソッドでdatetime64型に変換して扱いやすくします。

df_Jap['日付（datetime64）'] = pd.to_datetime(df_Jap['日付'], errors='coerce')
import datetime as dt
Train_Jap=df_Jap[(dt.datetime(2020,7,14) <= df_Jap['日付（datetime64）']) & (df_Jap['日付（datetime64）']  <= dt.datetime(2020,11,30) )]
Test_Jap=df_Jap[(dt.datetime(2020,12,1) <= df_Jap['日付（datetime64）']) & (df_Jap['日付（datetime64）']  <= dt.datetime(2020,12,31) )]

Prophetを用いた学習

ProphetはFacebookが開発した時系列予測のライブラリで詳細は以下に書かれてます。
https://facebook.github.io/prophet/docs/quick_start.html

特徴：

• Prophetの入力は列がdsとyのデータフレームである必要がある
• dsはデートスタンプ（日付）、yは予測を行いたい数値測定データ

Prophetで使えるようにリネーム：

Train_Jap=Train_Jap[["日付","国内の感染者数_1日ごとの発表数"]].rename(columns={"日付":"ds","国内の感染者数_1日ごとの発表数":"y"})
Test_Jap=Test_Jap[["日付","国内の感染者数_1日ごとの発表数"]].rename(columns={"日付":"ds","国内の感染者数_1日ごとの発表数":"y"})

Prophetの設定

Prophetのモデルをトレーニングデータ(Train_Jap)に対し学習させ、テストデータ(Test_Jap)に対し予測させますが、以下の設定ができます。

• growth

growth='linear'(線型)とgrowth='logistic'(ロジスティック関数)を選択できます。
growth='logistic'ではデータの上限（'cap'(環境収容力)）と下限を設定でき、ここではこちらを使います。
'cap'はグラフの見易さを理由にここでは10000とします。（１日の感染者数が10000人を超えない限りこれでいいです）

Train_Jap['cap']=10000
Test_Jap['cap']=10000

• changepoints

トレンドの変化点として
'2020/8/7', '2020/9/7', '2020/10/24', '2020/11/20'
を設定します。（グラフから目で読み取りました）

• seasonality_mode

seasonality_mode='additive'(加法的季節性)
seasonality_mode='multiplicative'(乗法的季節性)
の二つが選べますが、上のグラフを見ると週周期性が感染者数に比例して大きくなっているため、乗法的季節性の方を採用します。

• seasonality_prior_scale

モデルの周期性をデータにフィットさせる度合いを調整するパラメータです。
まず暫定的に1としますが、後にグリッドサーチで複数の値を入れてみます。

• changepoint_prior_scale

トレンド項の事前分布であるラプラス分布の分散を表しており、大きければ大きいほど変化点が検出されやすくなります。この項を大きくし過ぎると、かなり多くのポイントが変化点として検知されます。
まず暫定的に1としますが、後にグリッドサーチで複数の値を入れてみます。

情報元：
https://www.atmarkit.co.jp/ait/articles/1906/07/news004_2.html

• interval_width

不確定性区間の幅を表し、デフォルトでは0.8です。
こちらも後にグリッドサーチで複数の値を入れてみます。

学習の実行

model=Prophet(growth='logistic', seasonality_mode='multiplicative', seasonality_prior_scale=1, changepoint_prior_scale=1, changepoints=['2020/8/7', '2020/9/7', '2020/10/24', '2020/11/20'])
model.fit(Train_Jap)
forecast = model.predict(Test_Jap)
fig = model.plot_components(forecast)

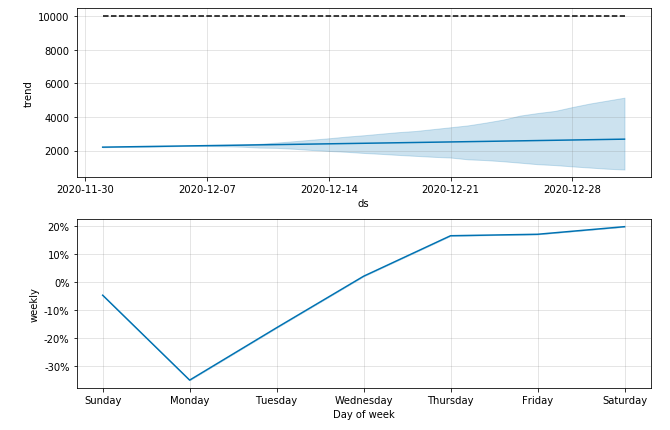
トレンド（年周期と週周期の変化の除いた動き）と週周期の学習結果が出ました↓
年周期はデータが１年分ないため表示されません。
日曜の検査数が少ないため月曜は感染者数が少なくなるのは知っていましたが、逆に木金土は多くなるといった傾向があるようです：

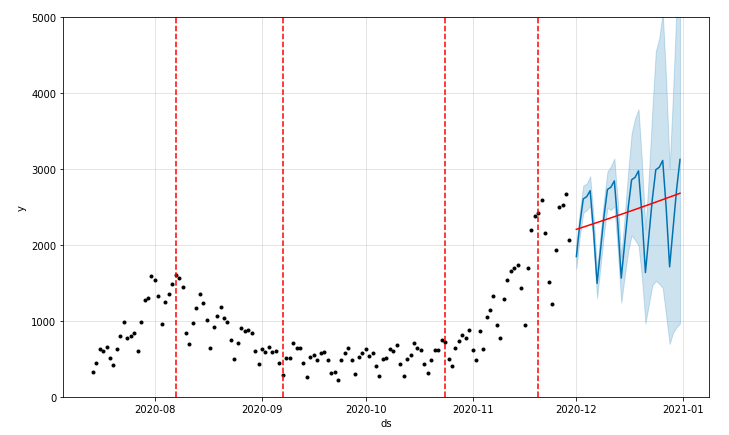
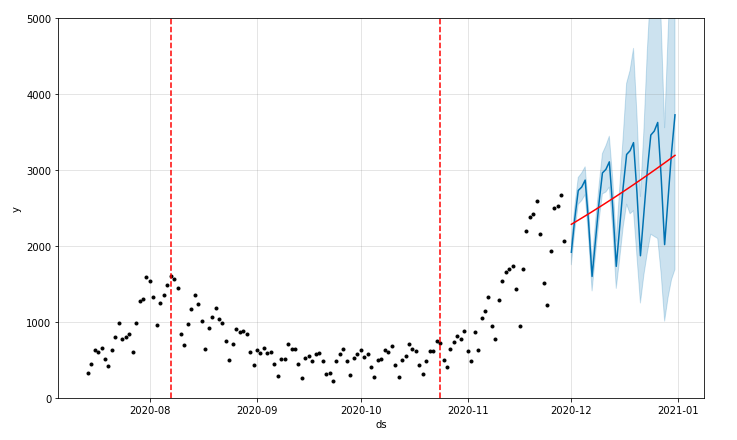
トレーニングデータと予測結果を表示します。
設定したトレンドの変化点を赤い破線、予測のトレンドの線を赤線、予測結果を青線で表示します。

from fbprophet.plot import add_changepoints_to_plot
plot = model.plot(forecast)
a = add_changepoints_to_plot(plot.gca(), model, forecast)
plt.ylim([-0, 5000])

学習によって得られた予測値yhatをTest_Japに列として追加します：

Test_Jap['yhat']=forecast['yhat'].values

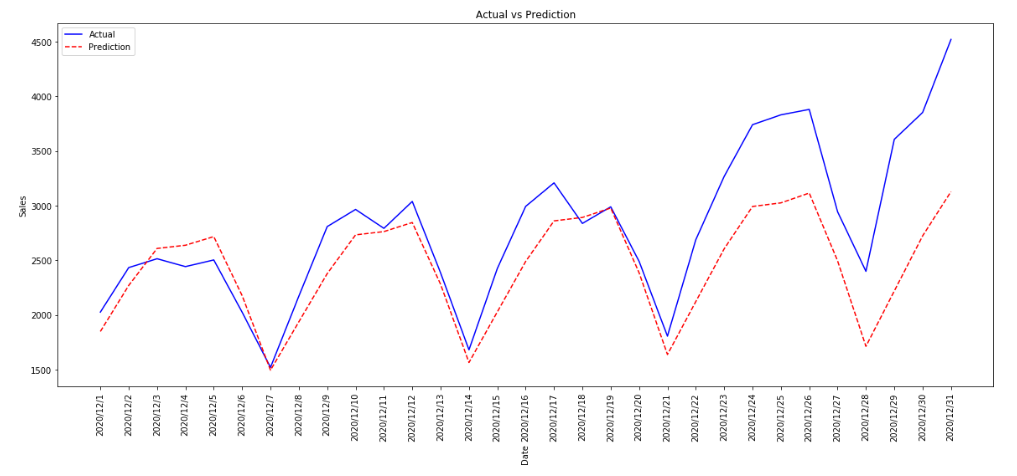
12月の実際の感染者数と予測結果を比較します：

plt.figure(figsize=(20, 8))
plt.plot(Test_Jap['ds'], Test_Jap['y'], 'b-', label = 'Actual')
plt.plot(Test_Jap['ds'], Test_Jap['yhat'], 'r--', label = 'Prediction')
plt.xlabel('Date',rotation=90); plt.ylabel('Sales'); plt.title('Actual vs Prediction')
plt.xticks(rotation=90)
plt.legend();

accuracyを計算してみます：

Test_Jap['diff']=(Test_Jap.y-Test_Jap.yhat).abs()
acc_ts2=(1-(Test_Jap['diff'].sum()/Test_Jap['y'].sum()))*100
acc_ts2

# 85.55183564855452

今回のaccuracyは約86%となりました。
さらに指標として
MAE（Mean Absolute Error：平均絶対誤差）
MSE（Mean Squared Error：平均二乗誤差）
RMSE（Root Mean Square Error:平均平方二乗誤差）
を計算してみます。

MAE_ts=metrics.mean_absolute_error(Test_Jap['y'], Test_Jap['yhat'])
MSE_ts=metrics.mean_squared_error(Test_Jap['y'], Test_Jap['yhat'])
RMSE_ts=np.sqrt(metrics.mean_squared_error(Test_Jap['y'], Test_Jap['yhat']))
print('MAE:', MAE_ts)
print('MSE:', MSE_ts)
print('RMSE:', RMSE_ts)

MAE: 404.44140578238205
MSE: 305342.084316079
RMSE: 552.5776726543328

すでに悪くないと思いますが、以下でグリッドサーチによりパラメータチューニングを行います。

グリッドサーチ

'changepoint_prior_scale'、'seasonality_prior_scale'、および'interval_width'について以下の値を設定しました。

params_grid = {'changepoint_prior_scale':[0.1, 0.5, 1, 2, 10],
               'seasonality_prior_scale':[0.1, 0.5, 1, 2, 10],
               'interval_width':[0.8, 0.85, 0.9, 0.95]
              }
grid = ParameterGrid(params_grid)

model_parameters = pd.DataFrame(columns = ['Acc','Parameters'])
for p in tqdm(grid):
    
    Train=Train_Jap.copy()
    Valid=Test_Jap[['ds','y','cap']].reset_index()
            
    m=Prophet(growth='logistic', 
              seasonality_mode='multiplicative', 
              seasonality_prior_scale=p['seasonality_prior_scale'], 
              changepoint_prior_scale=p['changepoint_prior_scale'], 
              changepoints=['2020/8/7', '2020/9/7', '2020/10/24', '2020/11/20'],
              interval_width = p['interval_width']
             )
            
    m.fit(Train_Jap)
            

    forecast = m.predict(Valid[['ds','cap']])
    forecast = forecast.astype({"ds": object,"cap": object})
    Valid=pd.concat([Valid.reset_index()[['ds','y']],forecast['yhat']], axis=1)
    
    #performance metric
    Valid['diff']=(Valid.y-Valid.yhat).abs()
    acc=(1-((Valid['diff'].sum()/Valid['y'].sum())))*100
    
    model_parameters = model_parameters.append({'Acc':acc,'Parameters':p},ignore_index=True)
            
parameters = model_parameters.sort_values(by=['Acc'],ascending=False)
parameters = parameters.reset_index(drop=True)
        
best_parameters=parameters['Parameters'][0]

ベストパラメータは
'changepoint_prior_scale': 0.5,
'interval_width': 0.8,
'seasonality_prior_scale': 2
となりました。これらのパラメータを使って改めてグラフ描画やaccuracy計算をしてみます。

m = Prophet(growth='logistic', 
            seasonality_mode='multiplicative', 
            seasonality_prior_scale=best_parameters['seasonality_prior_scale'],
            changepoint_prior_scale=best_parameters['changepoint_prior_scale'],
            changepoints=['2020/8/7', '2020/9/7', '2020/10/24', '2020/11/20'],
            interval_width =best_parameters['interval_width']
            )
m.fit(Train_Jap)
forecast=m.predict(Test_Jap)

from fbprophet.plot import add_changepoints_to_plot
plot = model.plot(forecast)
a = add_changepoints_to_plot(plot.gca(), model, forecast)
plt.ylim([-0, 5000])

Test_Jap['yhat']=forecast['yhat'].values
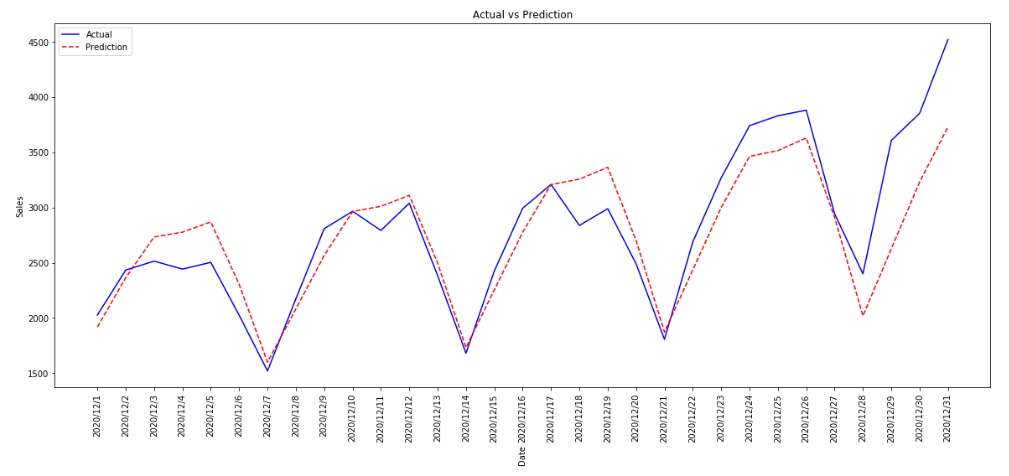
plt.figure(figsize=(20, 8))
plt.plot(Test_Jap['ds'], Test_Jap['y'], 'b-', label = 'Actual')
plt.plot(Test_Jap['ds'], Test_Jap['yhat'], 'r--', label = 'Prediction')
plt.xlabel('Date',rotation=90); plt.ylabel('Sales'); plt.title('Actual vs Prediction')
plt.xticks(rotation=90)
plt.legend();

Test_Jap_best['diff']=(Test_Jap_best.y-Test_Jap_best.yhat).abs()
acc_ts2=(1-(Test_Jap_best['diff'].sum()/Test_Jap_best['y'].sum()))*100
acc_ts2

# 90.92890097106074

accuracyは約91%で、MAE、MSE、およびRMSEは以下のようになりました。

MAE_ts=metrics.mean_absolute_error(Test_Jap['y'], Test_Jap['yhat'])
MSE_ts=metrics.mean_squared_error(Test_Jap['y'], Test_Jap['yhat'])
RMSE_ts=np.sqrt(metrics.mean_squared_error(Test_Jap['y'], Test_Jap['yhat']))
print('MAE:', MAE_ts)
print('MSE:', MSE_ts)
print('RMSE:', RMSE_ts)

# MAE: 253.92347110782634
# MSE: 111763.48089497152
# RMSE: 334.31045585648604

ランダムフォレスト回帰を用いた学習

ランダムフォレスト回帰を用いるにあたり、説明変数（ここではコロナの患者数に影響を与えると考えられる変数）として月と日と曜日を用いることにします。

ここで説明変数としてPCR検査数や海外からの渡航者数を用いると精度が上がるかもしれませんが、現在より先のコロナ患者数を予測する場合、そういったデータは使用できないため、ここでは使用しません。

def create_date_features(df):
    df['月']=df['日付（datetime64）'].dt.month
    df['日']=df['日付（datetime64）'].dt.day
    df['曜日（番号）'] = df['日付（datetime64）'].dt.weekday
    return df

reg_Jap=create_date_features(df_Jap)

def getdayofweek(day):
    if (day == 0):
        return "月曜"
    elif(day == 1):
        return "火曜"
    elif(day ==2):
        return "水曜"
    elif(day == 3):
        return "木曜"
    elif(day ==4):
        return "金曜"
    elif(day == 5):
        return "土曜"
    elif(day ==6):
        return "日曜"

reg_Jap['曜日'] = reg_Jap['曜日（番号）'] .apply(getdayofweek)
reg_Jap=pd.get_dummies(reg_Jap,columns=['曜日'])
reg_Jap

トレーニングデータ：

Train_reg_Jap=reg_Jap[(dt.datetime(2020,7,14) <= reg_Jap['日付（datetime64）']) & (reg_Jap['日付（datetime64）']  <= dt.datetime(2020,11,30) )]
x_train_reg_Jap=Train_reg_Jap[['月','日','曜日_月曜','曜日_火曜','曜日_水曜','曜日_木曜','曜日_金曜','曜日_土曜','曜日_日曜']]
y_train_reg_Jap=Train_reg_Jap[['国内の感染者数_1日ごとの発表数']]

テストデータ：

Test_reg_Jap=reg_Jap[(dt.datetime(2020,12,1) <= reg_Jap['日付（datetime64）']) & (reg_Jap['日付（datetime64）']  <= dt.datetime(2020,12,31) )]
x_test_reg_Jap=Test_reg_Jap[['月','日','曜日_月曜','曜日_火曜','曜日_水曜','曜日_木曜','曜日_金曜','曜日_土曜','曜日_日曜']]
y_test_reg_Jap=Test_reg_Jap[['国内の感染者数_1日ごとの発表数']]

学習を実行します。まずはパラメータとしてn_estimators=100だけ設定し、他はデフォルト値を使用します。

• n_estimators：決定木の数

ランダムフォレスト回帰のパラメータについてはこちらに記載されています。
https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestRegressor.html#sklearn.ensemble.RandomForestRegressor
：

rf_Jap = RandomForestRegressor(n_estimators=100)
rf_Jap.fit(x_train_reg_Jap,y_train_reg_Jap)
pred_rf = rf_Jap.predict(x_test_reg_Jap)

accuracyの計算：

y_test_reg_Jap['diff']=abs((y_test_reg_Jap['国内の感染者数_1日ごとの発表数'].values-pred_rf))
acc_rf=(1-(y_test_reg_Jap['diff'].sum()/y_test_reg_Jap['国内の感染者数_1日ごとの発表数'].sum()))*100
acc_rf

＃57.238258785021955

約57%という低い値になりまりました。

グリッドサーチ

• max_features：決定木の特徴量の数

　“auto”ならmax_features=n_features、
　“sqrt”ならmax_features=sqrt(n_features)、
　“log2”ならmax_features=log2(n_features)
　となる。

• min_samples_split：木を分割する際のサンプル数の最小数

• bootstrap：ブートストラップサンプリング（重複を許してランダムにデータを取り出す方法）の使用の有無

param_grid = { 
        "n_estimators"      : [10,20,300,100,200,500],
        "max_features"      : ["auto", "sqrt", "log2"],
        "min_samples_split" : [2,4,6,8],
        "bootstrap": [True, False],
            }
grid = ParameterGrid(param_grid)

model_parameters = pd.DataFrame(columns = ['Acc','Parameters'])
for p in tqdm(grid):
    
    X_Train=x_train_reg_Jap.copy()
    Y_Train=y_train_reg_Jap.copy()
    X_Valid=x_test_reg_Jap.copy()
    Y_Valid=y_test_reg_Jap.copy()
    m = RandomForestRegressor(n_estimators = p['n_estimators'],
               max_features = p['max_features'],
               min_samples_split = p['min_samples_split'],
               bootstrap=p['bootstrap']
        )
    
    m.fit(X_Train,Y_Train)
    pred_rf2 = m.predict(X_Valid)
            
    Y_Valid['yhat']=pred_rf2
    
    #performance metric
    Y_Valid_diff=(Y_Valid['国内の感染者数_1日ごとの発表数']-Y_Valid.yhat).abs()
    acc=(1-((Y_Valid_diff.sum()/Y_Valid['国内の感染者数_1日ごとの発表数'].sum())))*100
    
    model_parameters = model_parameters.append({'Acc':acc,'Parameters':p},ignore_index=True)
            
parameters = model_parameters.sort_values(by=['Acc'],ascending=False)
parameters = parameters.reset_index(drop=True)
        
best_parameters=parameters['Parameters'][0]

m2 = RandomForestRegressor(
        bootstrap=best_parameters['bootstrap'],
        max_features=best_parameters['max_features'],
        min_samples_split=best_parameters['min_samples_split'],
        n_estimators=best_parameters['n_estimators']
        )
m2.fit(x_train_reg_Jap,y_train_reg_Jap)
pred_rf2 = m2.predict(x_test_reg_Jap)

y_test_reg_Jap_diff2=abs((y_test_reg_Jap['国内の感染者数_1日ごとの発表数'].values-pred_rf2))
acc_rf2=(1-(y_test_reg_Jap_diff2.sum()/y_test_reg_Jap['国内の感染者数_1日ごとの発表数'].sum()))*100
acc_rf2

# 57.96572037955858

ベストパラメータを使っても先ほどの約57%とほとんど変わりませんでした。
また、ランダムフォレスト回帰ではランダム性があるため、上記のコードでベストパラメータの方がaccuracyが下回るケースも見られました。

XGBoostを用いた学習

XGBoost (extreme gradient boosting)とは、勾配ブースティングの一種で、１つ前までの決定木の結果を利用して新たな決定木を作る際に、実測値と予測値との誤差を用いているのが特徴です。

XGBoostのパラメータについてはこちらに記載されています。
https://xgboost.readthedocs.io/en/latest/parameter.html

また、このサイトの解説がわかりやすかったです。
http://kamonohashiperry.com/archives/209

• nthread：計算に用いる並列なスレッドの数
• learning_rate：学習率
• max_depth：決定木の最大深さ
• min_child_weight：子ノードにおけるデータの重み付けの合計値の最小の値
• subsample：各木においてランダムに抽出される標本の割合
• colsample_bytree：各木においてランダムに抽出される列の割合

データはランダムフォレスト回帰で用いたx_train_reg_Jap、y_train_reg_Jap、x_test_reg_Jap、およびy_test_reg_Japを使います。（説明変数は月と日と曜日です）

学習の実行：

xgb_Jap = XGBRegressor(n_estimators=100)
xgb_Jap.fit(x_train_reg_Jap,y_train_reg_Jap)
xgb_pred = xgb_Jap.predict(x_test_reg_Jap)

accuracyの計算：

y_test_reg_us['diff']=(y_test_reg_us['国内の感染者数_1日ごとの発表数']-xgb_pred).abs()
acc_xg=(1-(y_test_reg_us['diff'].sum()/y_test_reg_us['国内の感染者数_1日ごとの発表数'].sum()))*100
acc_xg
# 57.22788239483825

グリッドサーチ

param_grid = { 
            'nthread':[4], #when use hyperthread, xgboost may become slower,
            'learning_rate': [.03, 0.05, .07], #so called `eta` value
            'max_depth': [5, 6, 7],
            'min_child_weight': [1,4],
            'subsample': [0.7],
            'colsample_bytree': [0.7],
            'n_estimators': [100,200,500]
            }
grid = ParameterGrid(param_grid)

model_parameters = pd.DataFrame(columns = ['Acc','Parameters'])
for p in tqdm(grid):
    
    X_Train=x_train_reg_Jap.copy()
    Y_Train=y_train_reg_Jap.copy()
    X_Valid=x_test_reg_Jap.copy()
    Y_Valid=y_test_reg_Jap.copy()
    m = XGBRegressor(nthread = p['nthread'],
               learning_rate = p['learning_rate'],
               max_depth=p['max_depth'],
               min_child_weight = p['min_child_weight'],
               subsample = p['subsample'],
               colsample_bytree=p['colsample_bytree'],
               n_estimators=p['n_estimators']             )
    
    
    
    m.fit(X_Train,Y_Train)
    pred_xg2 = m.predict(X_Valid)
            
    Y_Valid['yhat']=pred_xg2
    
    #performance metric
    Y_Valid['diff']=(Y_Valid['国内の感染者数_1日ごとの発表数']-Y_Valid.yhat).abs()
    acc=(1-((Y_Valid['diff'].sum()/Y_Valid['国内の感染者数_1日ごとの発表数'].sum())))*100
    
    model_parameters = model_parameters.append({'Acc':acc,'Parameters':p},ignore_index=True)
            
parameters = model_parameters.sort_values(by=['Acc'],ascending=False)
parameters = parameters.reset_index(drop=True)
        
best_parameters=parameters['Parameters'][0]

m = XGBRegressor(
        nthread=best_parameters['nthread'],
        learning_rate=best_parameters['learning_rate'],
        max_depth=best_parameters['max_depth'],
        min_child_weight=best_parameters['min_child_weight'],
        subsample=best_parameters['subsample'],
        colsample_bytree=best_parameters['colsample_bytree'],
        n_estimators=best_parameters['n_estimators']
        )
m.fit(x_train_reg_Jap,y_train_reg_Jap)
pred_xg2 = m.predict(x_test_reg_Jap)

y_test_reg_Jap['diff']=(y_test_reg_Jap['国内の感染者数_1日ごとの発表数']-pred_xg2).abs()
acc_xg2=(1-(y_test_reg_Jap['diff'].sum()/y_test_reg_Jap['国内の感染者数_1日ごとの発表数'].sum()))*100
acc_xg2

# 57.36199327011835

こちらも先ほどの値とベストパラメータがほとんど同じ値になりました。

まとめ

・Prophet
・ランダムフォレスト回帰
・XGBoost
の３つの手法において、2020年の7/14～11/30の日本のコロナ感染者数データを使ってモデルを学習させ、12/1～12/31の感染者数を予測させたところ、Prophetではaccuracyが約91%になりましたが、ランダムフォレスト回帰とXGBoostでは57%程度という低い値になりました。

説明変数として月と日と曜日だけしか使えなかったので無理もないと思います。

感想としては、Prophetというのは2Dグラフのパターンを読み取って予測してくれるものであり、今回のようなコロナ患者数の予測においてはランダムフォレスト回帰やXGBoostよりも向いていると思いました。