別の記事にて導出した曲率の公式について、Numpyを使って合ってるかどうか確かめます。
曲率
平面上の曲線に関して、ある点における曲がり具合を曲率といいます!
とはいえ実際のイメージは点ではなく極小区間における接線ベクトルの向きに関する変化率といえます!
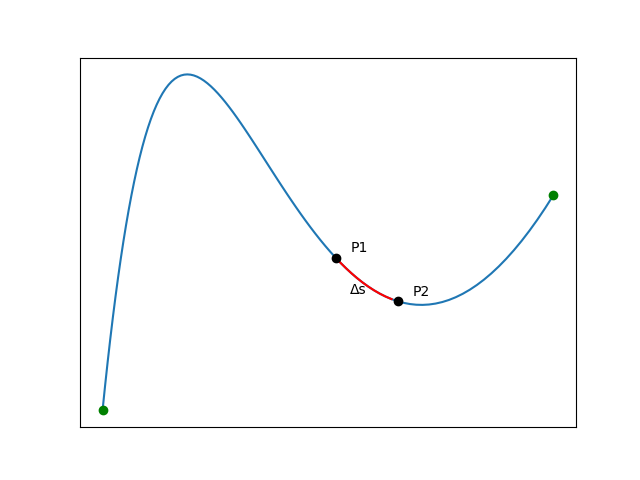
下図で言えば、極小区間Δsにおいて、P1における接線ベクトルとP2における接線ベクトルの向きがどれだけ変わったか、それを示すのが曲率です!
自分が知る限り、曲率を求める方法は大きく以下の二つがあります!
- ベクトルの垂直変化率の大きさから求める
- 円をフィッティングし、その円の半径の長さから求める
上ではベクトルの変化を用いて曲率を説明ましたが、この記事では、円フィッティングを用いた曲率の導出を行っていきます!
平面における曲率の求め方
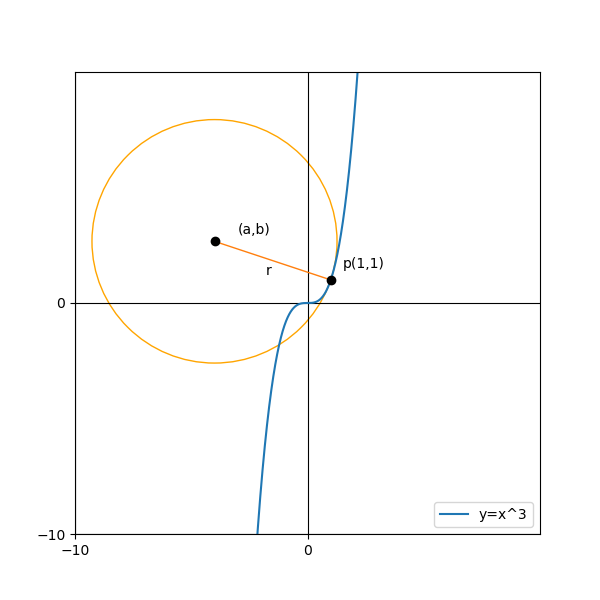
今、関数y=x^3に関して、点pにフィットする円を見つけたい。そんな気持ちです。
一般に、フィットする円の半径は曲率半径と呼ばれ、その逆数をとることで曲率が得られます。
関数について、y=f(x)と考えまして、x=cのとき点(c,f(c))をとります。
このとき、見つけたい円はきっと以下のような形をとっているはずです!
(c-a)^2+(f(c)-b)^2=r^2
上は、円の方程式にc,f(c)を代入した形です!
微分したり色々したりしてa,b,rそれぞれについて解くと以下のような公式が導かれます!
\begin{align}
a&=c-\frac{1+f'(c)^2}{f''(c)}・f'(c)\\
b&=f(c)+\frac{1+f'(c)^2}{f''(c)}\\
r&=\frac{{\bigl(1+f'(c)^2\bigr)}^\frac{3}{2}}{|f''(c)|}
\end{align}
そして、お目当ての曲率κ(カッパ)は、曲率半径の逆数をとればよいので・・・
κ=\frac{|f''(c)|}{{\bigl(1+f'(c)^2\bigr)}^\frac{3}{2}}
このようになります。
これを使って図の円についてそれぞれの値を求めると、以下のようになります!
a=-4\quad b=\frac{8}{3}\fallingdotseq2.67\quad r=\frac{5\sqrt{10}}{3}\fallingdotseq5.27\quad κ\fallingdotseq0.19
さて、ここまでで扱った式は、yがxに関する式で表せる、すなわちy=f(x)の形式がとれている状況を前提としています。
では、次のような平面曲線はどのような式で表されるでしょうか?
私は、このようなとってもかわいらしい一筆書きニコちゃんマークを表す関数を知りません。
ですが、このような曲線でも、しっかりと平面上の関数として表す方法があります。
それが媒介変数表示です!媒介変数表示は以下のような形式をとります。
\left\{
\begin{array}{ll}
x = f(t) \\
y = g(t)
\end{array}
\right.
y=ほにゃららxみたいな感じではなく、媒介変数(ここではt)というx,yを繋ぐ時系列的な要素を用いて、x,yを2つの式によって表しています。
f(t),g(t)を使って曲率半径及び曲率を表現できれば、すべての平面曲線においての曲率を求めることが出来るはずです!
つきましては、地獄のような苦しみを乗り越え既に公式を導出していますのでご紹介します。
曲率半径r\qquad r=\frac{\bigl(f'(t)^2+g'(t)^2\bigr)^\frac{3}{2}}{|f'(t)g''(t)-f''(t)g'(t)|}
曲率κ\qquad κ=\frac{|f'(t)g''(t)-f''(t)g'(t)|}{\bigl(f'(t)^2+g'(t)^2\bigr)^\frac{3}{2}}
これが媒介変数表示を使って表された曲率半径r及び曲率κになります。とってもシンプルですね!!!!!!!!!!!
導出しただけで式が本当に合っているかまでは確かめていなかったので、今回はnumpyを使ってそれを確認しようという算段です!
ではy=x^3に再び登場してもらいます。
この曲線に関して、以下の式によって求められた曲率の値が一致していれば、導出した公式はおおむね正しいことになります。
y=f(x)が前提となる公式\qquadκ=\frac{|f''(c)|}{{\bigl(1+f'(c)^2\bigr)}^\frac{3}{2}} ・・・①
媒介変数表示を使った公式\qquad κ=\frac{|f'(t)g''(t)-f''(t)g'(t)|}{\bigl(f'(t)^2+g'(t)^2\bigr)^\frac{3}{2}} ・・・ ②
さっそくpythonプログラムを作っていきましょう。
まずは必要なものをインポート
import numpy as np
import matplotlib.pyplot as plt
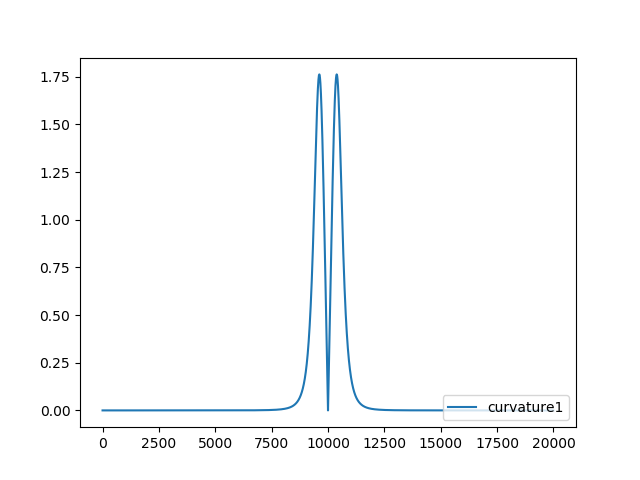
最初に、①によって生成される曲率グラフを見てみます。
x,yの値を設定
x = np.arange(-10,10,0.001)
y = x ** 3
公式①をnumpyで表現。なんとnumpyちゃんは座標データの傾きを求める(=微分する)というとっても素晴らしい関数を持っています。
dif_y = np.gradient(y,x) # xに関して微分
dif2_y = np.gradient(dif_y,x)
curvature = np.abs(dif2_y) / (1 + (dif_y)**2)**1.5
曲率グラフをプロット
plt.plot(np.arange(0,curvature.size,1),curvature,label="curvature1")
plt.legend(loc='lower right')
plt.show()
↓こんな感じになります
では公式②のほうを見てみます。
同じようにインポートから
import numpy as np
import matplotlib.pyplot as plt
x,yの値を同じように設定
x = np.arange(-10,10,0.001)
y = x ** 3
公式②をnumpyで表現。
dif_x = np.gradient(x) # 第二引数がない場合、時系列で微分
dif_y = np.gradient(y)
dif2_x = np.gradient(dif_x)
dif2_y = np.gradient(dif_y)
curvature = np.abs(dif2_x * dif_y - dif_x * dif2_y) / (dif_x **2 + dif_y **2)**1.5
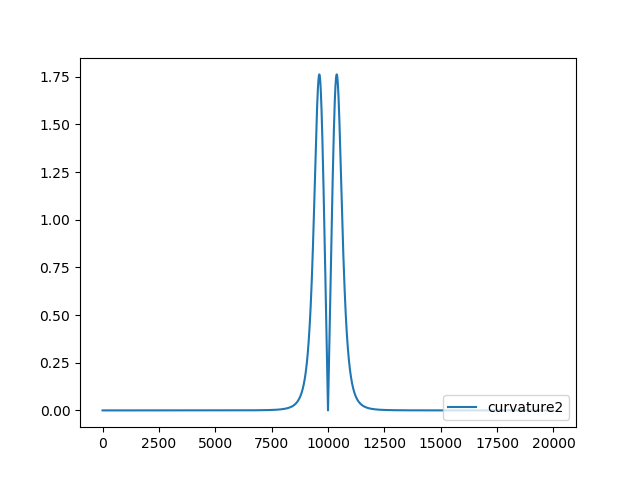
それではドキドキのプロット
plt.plot(np.arange(0,curvature.size,1),curvature,label="curvature2")
plt.legend(loc='lower right')
plt.show()
やったぜ。
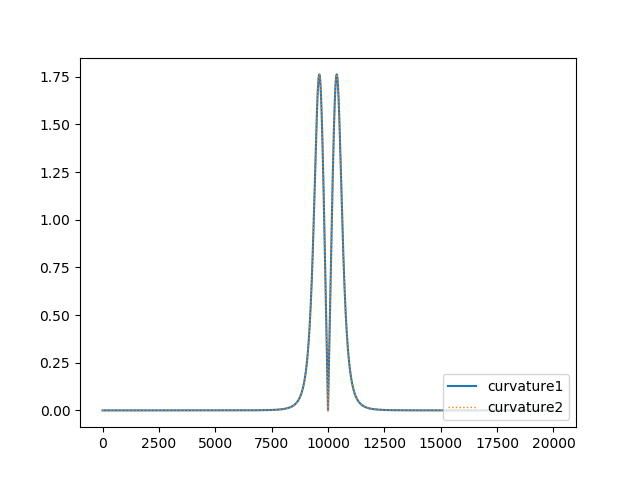
二つを重ねてみます。
分かりづら!でもまあ一致してますよね!
ということでxとyの関係式が存在しない場合でも、時系列の座標データさえあれば媒介変数の考えのもと曲率を求められることが分かりました。
今回は-10<=x<=10という狭い区間で座標点を20000ほど用意していますのできれいに曲率が求められているように見えますが、より高い精度を求める場合はこの公式の利用は推奨しません。。。
本来は時系列ではなく、距離に基づく関数を用いて曲率を求める必要があります。(これについては前回の記事でちょっとだけ詳しく書いております。)
CODE
使ったコードを置いておきます。
import numpy as np
import matplotlib.pyplot as plt
def culcCurvature1(x,y):
dif_y = np.gradient(y,x)
dif2_y = np.gradient(dif_y,x)
curvature = np.abs(dif2_y) / (1 + (dif_y)**2)**1.5
return curvature
def culcCurvature2(x,y):
dif_x = np.gradient(x)
dif_y = np.gradient(y)
dif2_x = np.gradient(dif_x)
dif2_y = np.gradient(dif_y)
curvature = np.abs(dif2_x * dif_y - dif_x * dif2_y) / (dif_x **2 + dif_y **2)**1.5
return curvature
if __name__ == '__main__':
x = np.arange(-10,10,0.001)
y = x ** 3
cuv1 = culcCurvature1(x,y)
cuv2 = culcCurvature2(x,y)
#plt.plot(np.arange(0,cuv1.size,1),cuv1,label="curvature1")
#plt.plot(np.arange(0,cuv2.size,1),cuv2,label="curvature2")
#plt.legend(loc='lower right')
#plt.show()