がんばってみました。
曲率
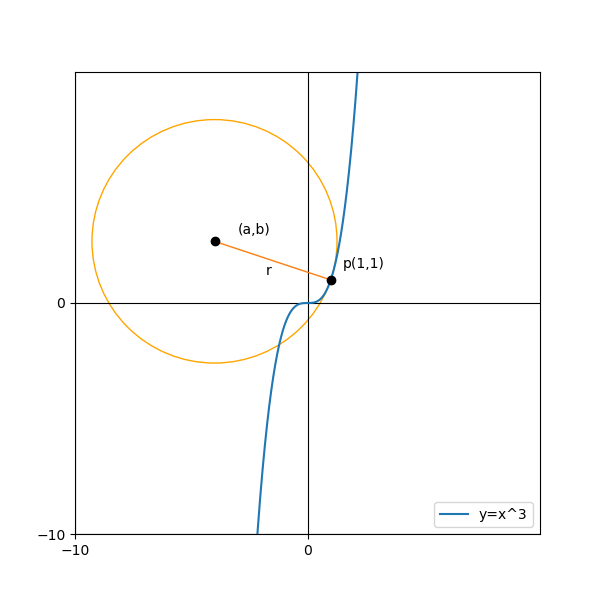
曲率…すなわち曲線上のある点におけるの曲がり具合は、その点においてフィットする円を把握することで求めることが出来ます。フィットする円の半径は曲率半径と呼ばれ、その逆数をとることで曲率が得られます!
一般的な曲率の求め方
上の図で言えば、y=x^3という曲線(関数)に対して、p(1,1)においてフィットする円が存在し、その円の半径rが曲率半径であり、1/rが曲率となります!
現在円に関して分かる情報は「関数y=x^3上の点pでフィットする」ということ。ですので曲率半径rを求めるためには、円の方程式中のr以外の数をx,yで表せばよいということになります。
さて、円の方程式は一般に以下の形で知られています!
円の方程式\\ (x-a)^2+(y-b)^2=r^2
この方程式をどうにかして、x-aとy-bの部分について、a,bを使わないxとyだけの式で表すことが出来れば、rを求めることが出来るはずです!
とりあえず2乗が邪魔なので、それを消すために微分してみましょう。xに関して微分を行うと、以下の形をとります!
1次微分 \\(x-a)+(y-b)・y'=0 ・・・ ①
2次微分 \\1+(y')^2+(y-b)・y''=0 ・・・ ②
②ではaが消えているので、既にy-bを求める事が可能となっています!
が、ここは順番的にx-aから求めていきましょう!
①\times y''-②\times y'より、\\
(x-a)・y''-\bigl(1+(y')^2\bigr)・y'=0\\
x-a=\frac{1+(y')^2}{y''}・y' ・・・ ①'
続いてy-b
②より、\\
y-b=-\frac{1+(y')^2}{y''} ・・・ ②'
円の方程式の左辺が求められましたが、これでは変形しただけですね・・・!
後々のために、形式をy=x^3に対応させていきましょう!
yを関数f(x)と定義します!
y=f(x)=x^3に関して、x=cのとき、点\bigl(c,f(c)\bigr)をとる
そうなると①'と②'は以下のように置き換えられます。
c-a=\frac{1+f'(c)^2}{f''(c)}・f'(c) ・・・ ③\\
f(c)-b=-\frac{1+f'(c)^2}{f''(c)} ・・・ ④\\
これで中心座標が(a,b)で、関数y=x^3上の点(c,f(c))においてフィットする円の半径rを求めることが出来ます。
③、④から\\
\begin{align}
r^2&=\frac{1}{f''(c)}\Bigl(\bigl(1+f'(c)^2\bigr)^2・f'(c)+\bigl(1+f'(c)^2\bigr)\Bigr)\\
&=\frac{1}{f''(c)}\Bigl(\bigl(1+f'(c)^2)^2\bigr)\bigl(f'(c)+1\bigr)\Bigr)\\
&=\frac{1}{f''(c)}\bigl(1+f'(c)^2\bigr)^3
\end{align}
\\
よって、曲率半径rはr>0より、\\
r=\frac{{\bigl(1+f'(c)^2\bigr)}^\frac{3}{2}}{|f''(c)|}\\
\\
曲率κ=1/rは、\\
κ=\frac{|f''(c)|}{{\bigl(1+f'(c)^2\bigr)}^\frac{3}{2}}\\
となる。
これで目的の曲率を求めることが出来るようになりました。
曲率は一般に**κ(カッパ)**で表されるそうなので、例に従ってみました。
ちなみに、この場合のa,b,r,κは以下のような値をとるようです。(計算式省略)
a=-4\quad b=\frac{8}{3}\fallingdotseq2.67\quad r=\frac{5\sqrt{10}}{3}\fallingdotseq5.27\quad κ\fallingdotseq0.19
しかし、これはあくまで曲線がy=f(x)の形で表すことができる前提の公式です・・・・・・
一般的に登場する多くの曲線はむしろそのような式で表すことが困難で、代わりに以下のような形をとります!
\left\{
\begin{array}{ll}
x = f(t) \\
y = g(t)
\end{array}
\right.
この形式は媒介変数表示、またはパラメータ表示と呼ばれています。高校で習いましたね!
tは媒介変数ですが、時系列と思うと簡単にイメージできます。f(t),g(t)に対して、同じtが入れば同じタイミングのx,y座標が得られます!
さて、ここでやっと本題になりますが、この媒介変数表示で与えられたxのtについての関数f(t)と、yのtについての関数g(t)を用いて、↑の公式を一般化していきます!(一般化でいいのかわかんないけど一般化していきます!!!)
媒介変数表示された平面曲線の曲率の求め方
先述のとおり、以下のように媒介変数tを用いて媒介変数表示された平面曲線に関して、曲率を求める公式を導出していきます。頑張ります!
\left\{
\begin{array}{ll}
x = f(t) \\
y = g(t)
\end{array}
\right.
ちなみに、自分が知る限り媒介変数表示を用いることでxy平面上に存在するすべての曲線を表すことができます。たぶん。
なので、この条件で曲率が求められたならば、(時系列ごとのxy座標データさえ持っていれば)全ての平面曲線の曲率を求めることが出来ます。きっと。
それでは結果が出る事を祈って、計算を始めていきます。
円の方程式\\ (x-a)^2+(y-b)^2=r^2
↑の方式で円の方程式を基点として公式の導出をしていたので、同じ形式をとりましょう。そして今回は最初からx=f(t),y=g(t)を代入していきます!
(f(t)-a)^2+(g(t)-b)^2=r^2
同じように微分してみます!tに関してやってみますか!
(f(t)-a)・f'(t)+(g(t)-b)・g'(t)=0
こんな形になりました。なんだこれ!
aを消したいので、(f(t)-a)にひっついているf'(t)で両辺を割ります!
(f(t)-a)+\frac{g'(t)}{f'(t)}・(g(t)-b)=0 ・・・ ①
この状態で、tに関してもう一度微分します。これでaが消えるな!
f'(t)+\biggl(\frac{g'(t)}{f'(t)}\biggr)'・(g(t)-b)+\frac{g'(t)}{f'(t)}・g'(t)=0 ・・・ ②
これほんとに収拾つくの?
・・・似てる部分があるので、とりあえず①と②を統合してみます。
①\times\biggl(\frac{g'(t)}{f'(t)}\biggr)'-②\times\frac{g'(t)}{f'(t)}より、\\
\biggl(\frac{g'(t)}{f'(t)}\biggr)'(f(t)-a)-\frac{g'(t)}{f'(t)}・f'(t)-\biggl(\frac{g'(t)}{f'(t)}\biggr)^2・g'(t)=0
ぐっちゃぐちゃ
f(t)-a=\frac{\biggl(\frac{g'(t)}{f'(t)}\biggr)(f'(t)+\frac{g'(t)}{f'(t)}・g'(t))}{\biggl(\frac{g'(t)}{f'(t)}\biggr)'} ・・・ ③
w
②より、\\
g(t)-b=-\frac{f'(t)+\frac{g'(t)}{f'(t)}・g'(t)}{\biggl(\frac{g'(t)}{f'(t)}\biggr)'} ・・・ ④
・・・w
絶望感しかありませんが、合っていることを信じて曲率半径rを求めてみます。ウオオオオオオオ!
(f(t)-a)^2+(g(t)-b)^2=r^2について、③と④を用いて、\\
\begin{align}
r^2&=\Biggl(\frac{\biggl(\frac{g'(t)}{f'(t)}\biggr)(f'(t)+\frac{g'(t)}{f'(t)}・g'(t))}{\biggl(\frac{g'(t)}{f'(t)}\biggr)'}\Biggr)^2+\Biggl(-\frac{f'(t)+\frac{g'(t)}{f'(t)}・g'(t)}{\biggl(\frac{g'(t)}{f'(t)}\biggr)'}\Biggr)^2\\
&=\frac{1}{\Biggl(\biggl(\frac{g'(t)}{f'(t)}\biggr)'\Biggr)^2}\Biggl(\biggl(\frac{g'(t)}{f'(t)}\biggr)^2(f'(t)+\frac{g'(t)}{f'(t)}・g'(t))^2+(f'(t)+\frac{g'(t)}{f'(t)}・g'(t))^2\Biggr)\\
&=\frac{1}{\Biggl(\biggl(\frac{g'(t)}{f'(t)}\biggr)'\Biggr)^2}・\biggl(f'(t)+\frac{g'(t)}{f'(t)}・g'(t)\biggl)^2・\Biggl(\biggl(\frac{g'(t)}{f'(t)}\biggr)^2+1\Biggr)\\
&=\frac{1}{\Biggl(\frac{\bigl(f'(t)g''(t)-f''(t)g'(t)\bigr)}{\bigl(f'(t)\bigr)^2}\Biggr)^2}・\biggl(f'(t)^2+2g'(t)^2+\frac{g'(t)^4}{f'(t)^2}\biggl)・\Biggl(\frac{g'(t)^2}{f'(t)^2}+1\Biggr)\\
&=\frac{f'(t)^4}{\bigl(f'(t)g''(t)-f''(t)g'(t)\bigr)^2}・\biggl(\frac{f'(t)^4+2f'(t)^2g'(t)^2+g'(t)^4}{f'(t)^2}\biggl)・\Biggl(\frac{g'(t)^2+f'(t)^2}{f'(t)^2}\Biggr)\\
&=\frac{f'(t)^4}{\bigl(f'(t)g''(t)-f''(t)g'(t)\bigr)^2}・\biggl(\frac{\bigl(f'(t)^2+g'(t)^2\bigr)^2\bigl(g'(t)^2+f'(t)^2\bigr)}{f'(t)^4}\biggl)\\
&=\frac{\bigl(f'(t)^2+g'(t)^2\bigr)^3}{\bigl(f'(t)g''(t)-f''(t)g'(t)\bigr)^2}
\end{align}
途中で5回ほど血反吐を吐きましたが。なんとかきれいな式を導けたかと思います。なんでf(t),g(t)のままやったんだろう・・・
↓絶望のMarkdown

ということで曲率半径r及び曲率κは以下のようになります。
曲率半径r\qquad r=\frac{\bigl(f'(t)^2+g'(t)^2\bigr)^\frac{3}{2}}{|f'(t)g''(t)-f''(t)g'(t)|}
曲率κ\qquad κ=\frac{|f'(t)g''(t)-f''(t)g'(t)|}{\bigl(f'(t)^2+g'(t)^2\bigr)^\frac{3}{2}}
これで、xy座標の時系列データさえあれば、平面曲線の曲率を求められるようになりました・・・!
と言いたいところですが、これにより求められる曲率はあくまで近似値になります><
それは媒介変数、つまり時系列によって表現される座標列が、曲線上において必ずしも等間隔の長さをとらないという事実に起因します。(走っている2台の車が、同じ時間で同じ距離進むとは限りませんよね!)
もちろん長さが違っていても、点と点の間隔が小さくなればなるほど精度は向上していきます!
次回は、今回求めた曲率半径及び曲率に関して、numpyを使って正しい結果が得られるかどうか見ていきます。