Wordleとは
最近、Wordleというゲームにハマっています。
https://www.powerlanguage.co.uk/wordle/
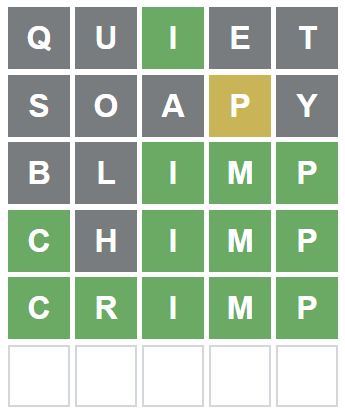
5文字の英単語を当てるゲームです。ルールをざっと説明すると以下の通り。
- 入力できる文字列は英単語だけ(無意味な文字列は入力できない)
- 文字列を入力できるチャンスは6回のみ
- 文字列入力後、各文字について、
- 外れた文字は灰色でハイライトされる
- 位置は異なるが含まれている文字は黄色でハイライトされる
- 当たった文字は緑色でハイライトされる
- すべての文字を緑色にすれば勝ち
ついでに、以下のような仕様がSNSでバズっている理由な気がします。
- 一日ごとに問題が変わる
- 同じ端末で解けるのは一日に一回
- Twitterに結果を簡単にコピペできる(文字列を伏せたまま)
正解がまったく聞いたこともない単語であることもままあり、かなり英語の語彙力を試されます。
楽しく英語を勉強したい方にはうってつけのゲームです。
初手で情報量を増やしたい
さて、Wordleに挑むときに悩ましい問題のひとつが、最初に何を入力するかです。
一手目はノーヒントなわけですから、いきなり正解するのはまず無理でしょう。
(SNSで一手目で正解した人を見かけたとしても、99%別の端末で先に解いて答えを知ってる人です)
その代わり、一手目ではより多くのヒント、より多くの情報量が得られるような文字列を入力したくなります。
この考えを推し進めて、もう少し理論的に定式化してみましょう。
情報についての理論ということで、情報理論の考え方を用います。
この考え方を説明するために、いったんWordleから離れて、もっと簡単な問題を考えてみましょう。
ここで例に出すのは、**「人当てゲーム」**です。
出題者が思い浮かべている特定の人物を、「YES/NO」で答えられる質問だけで当てていくゲームです。

(似たようなゲームで有名なものだと、ランプの魔人、Akinatorがありますね。
こちらの場合、プレイヤーは質問される側ですが。)
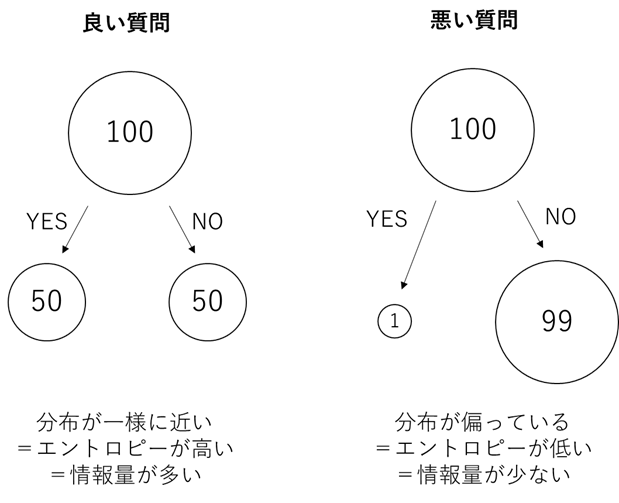
まず、「人当てゲーム」における最初の一手を考えてみましょう。
例えば、「あなたが思い浮かべている人物は**草刈正雄**ですか?」のように、いきなり個人名を出してしまうことが悪手だというのは、なんとなくわかることかと思います。
むしろ「あなたが思い浮かべている人物は男性ですか?」のように、最初の質問ではそこそこ多くの人に当てはまる属性を聞いていくのがスジだという気がします。
逆に言うと、「草刈正雄ですか?」がよくないのは、「草刈正雄ではない」というのがほとんどの人間に当てはまるから、NOの答えが返ってきて当然だから、ということです。
このように「ある属性(質問の答え)が集団の中で偏っていること」を、情報理論では「エントロピーが低い=平均情報量が少ない」と言います。
わかりやすいように、図にまとめておきます。
さて、同じ考えをWordleに応用してみましょう。
単語当てゲームであるところのWordleは、実は、人当てゲームとルールがよく似ています。
違いは、一度に交わされる質問と答えの数が多いという点だけです。
Wordleにおける1つの質問は、1文字の入力に相当します。
つまり、Wordleでは、5つの質問を同時にしていることになります。
そして、それぞれの質問に対し、YES/NOではなく、灰/黄/緑の3通りの答えが返って来るわけです。
人当てゲームでは、一回の質問によって、候補がYES/NOの2つの集団に分かれました。
Wordleでは、一回の質問によって、候補が3^5=243の集団に分かれることになります。
しかし、数が増えただけで、基本的な戦略は人当てゲームと同じように考えることができるでしょう。
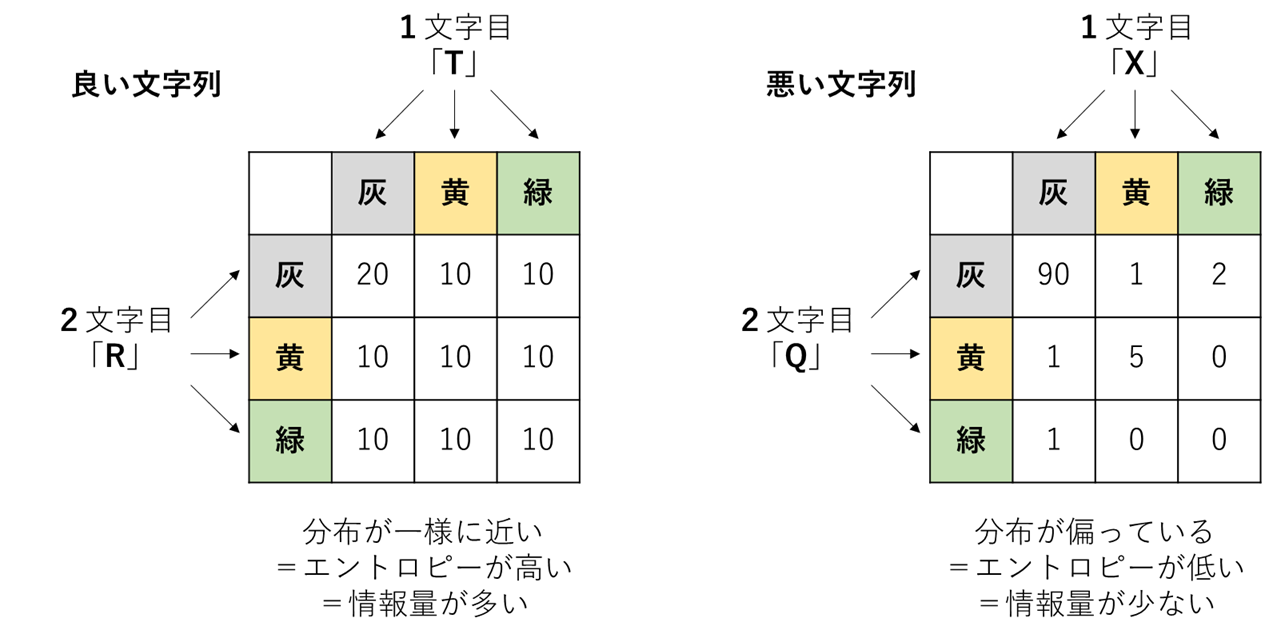
良い文字列とは、3^5=243の集団において答えの偏りが少ない=エントロピーが高い=情報量が多い文字列なのです。
再度、わかりやすいように、図にまとめておきます。
(5階のテンソルを視覚的に表示するのが大変なので、2文字目までの情報、つまり3^2=9の集団だけ以下には記しています)
以上をまとめると、**「Wordleの初手の最善手」とは、「最もエントロピーが高い文字列を出す」**ということになります。
(これはあくまでもナイーブな情報理論に基づいた考え方です。他の戦略もありえるでしょう)
最後に一応、情報理論的エントロピー=平均情報量を数式でちゃんと表しておきましょう。
分割数を$n$、$i$番目の分割された集団のサイズを$N_i$としたとき、エントロピー$H$は次のように定義されます。
H=\sum_{i=1}^n P_i (-\log P_i) \\
\text{where } P_i=\frac{N_i}{\sum_{i=1}^n N_i}
もちろん、ここで$P_i$は$i$番目の集団が選択される確率を意味します。
そして、$(-\log P_i)$がその事象の情報量(自己情報量、選択情報量)と呼ばれるものです。
情報量は$0\le P_i\le 1$に対して対数をとってからマイナスを掛けているので、必ず非負の値を取ります。
この情報量の集団平均を取ったものがエントロピー$H$ですから、平均情報量と呼ばれるのも納得です。
実装しよう、そうしよう
必要な理論は揃ったので、最もエントロピーが高い文字列を探すコードをPythonで実装しましょう。
Jupyter-labでの実行結果も適宜載せていきます。
フリー英和辞書のダウンロード
まずは、フリーの英和辞書をダウンロードします。
今回の目的上、日本語の部分はなくてもいいのですが、英単語の意味もわかると勉強になって楽しいです。
必要なライブラリ
データ解析に使う基本的なライブラリに加えて、scipyからエントロピーを計算する関数entropyをインポートします。
(この関数、合計が1になるように規格化されてないリストを与えても、ちゃんとエントロピーを計算してくれます)
あとは、並列計算用のjoblibも入れておきます。
import pandas as pd
import re
import numpy as np
from scipy.stats import entropy
from joblib import Parallel,delayed
Wordle用5文字辞書の作成
普通の辞書は5文字以外の単語とか、記号も含めた単語とか、見出しに大文字小文字が混ざった状態だったりするので、これらをWordle用に整えていきます。
eng_dict = pd.read_table("ejdict-hand-utf8.txt",header=None).rename(columns={0:"key",1:"value"})
eng_dict = eng_dict[[len(str(key))==5 for key in eng_dict["key"]]]
eng_dict = eng_dict[[True if re.match(r'[a-zA-Z]{5}', str(key)) else False for key in eng_dict["key"]]]
eng_dict["key"] = eng_dict["key"].str.upper()
eng_dict.drop_duplicates(subset="key",inplace=True)
eng_dict.set_index("key",inplace=True)
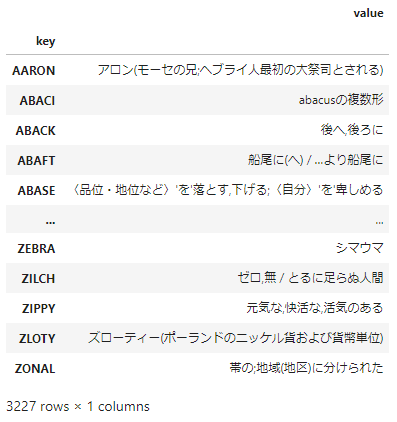
eng_dict
できあがった中身はこちら。
一文字ずつに分割
以降の解析をしやすいように、文字列を一文字ずつに分割して異なる列に収めたデータフレームを用意しておきます。
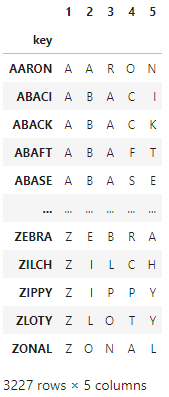
df_char = pd.DataFrame([list(key) for key in eng_dict.index],columns=range(1,6))
df_char.index=eng_dict.index
df_char
エントロピー計算
ここでようやく肝心のエントロピー計算です。エントロピー計算そのものは簡単なのですが、与えられた文字列に対して結果を3^5通りに分類するコードの部分が結構長くなってしまったので、表示を省略しておきます。
(もっと短く書く方法があったら教えて欲しい)
**エントロピー計算のコード (やや長いですが見たい方はここをクリック)**
def calc_cluster_entropy(df_char, input_word:str):
cluster_size = np.zeros(np.repeat(3,5))
Green = pd.DataFrame()
Yellow = pd.DataFrame()
Gray = pd.DataFrame()
for pos, char in enumerate(list(input_word)):
Green[pos] = (df_char[pos+1] == char)
Yellow[pos] = (~Green[pos])&(df_char.index.str.contains(char))
Gray[pos] = (~Yellow[pos]) & (~Green[pos])
for i in range(3):
if i==0:
TF_i = Gray[0]
elif i==1:
TF_i = Yellow[0]
else:
TF_i = Green[0]
for j in range(3):
if j==0:
TF_j = Gray[1]
elif j==1:
TF_j = Yellow[1]
else:
TF_j = Green[1]
for k in range(3):
if k==0:
TF_k = Gray[2]
elif k==1:
TF_k = Yellow[2]
else:
TF_k = Green[2]
for l in range(3):
if l==0:
TF_l = Gray[3]
elif l==1:
TF_l = Yellow[3]
else:
TF_l = Green[3]
for m in range(3):
if m==0:
TF_m = Gray[4]
elif m==1:
TF_m = Yellow[4]
else:
TF_m = Green[4]
cluster_size[i,j,k,l,m] = (TF_i&TF_j&TF_k&TF_l&TF_m).sum()
cluster_size = np.int64(cluster_size.ravel())
return entropy(cluster_size, base=2)
上記で作成した、「与えられた単語が作る分割集団のエントロピーを計算する関数」 calc_cluster_entropy を使って、「与えられた単語のリストをエントロピー順にソートして、日本語の意味を表示する関数」 order_by_entropy も作っておきます。
時間がかかるので、joblibで並列化しておきます。
def order_by_entropy(df_temp):
df_entropy = pd.DataFrame(Parallel(n_jobs=-1)(delayed(calc_cluster_entropy)(df_temp, index) for index in df_temp.index),
index=df_temp.index, columns=["entropy"])
df_entropy.sort_values("entropy",ascending=False,inplace=True)
df_entropy["meaning"]=eng_dict.loc[df_entropy.index,"value"]
return df_entropy
order_by_entropy(df_char)
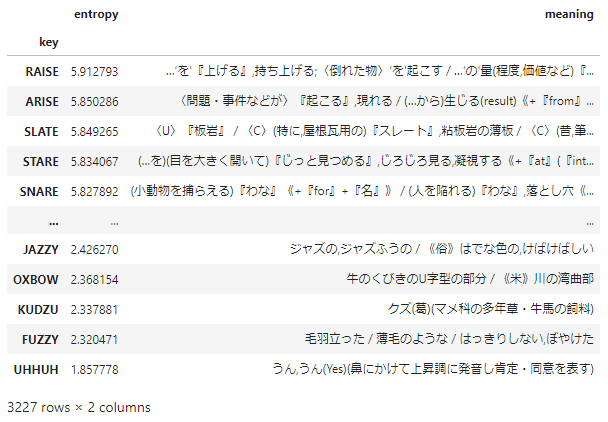
order_by_entropy に、先ほど作成した1文字ずつの辞書を与えた結果がこちらになります。
Wordleの初手の最善手
というわけで、Wordleの初手の最善手は**"RAISE"であることがわかりました。
誰でも知っている英単語ですね。忘れる心配はなさそうです。
私は今後、Wordleの初手はRAISE**で決め打ちすることにします!
ところで、推理小説の愛好家なら、**「英文では"E"が一番多く使われている」**というネタをよくご存知のことかと思います。
実は、今回作成した5文字辞書でも同じことが言えます。アルファベットを出現頻度順に並べるコードは以下の通り。
char2freq = pd.Series(df_char.values.ravel()).value_counts().to_dict()
char2freq
上位6文字の"O"以外の文字から構成された単語が最善手というのは、できるだけ黄色のヒットを当てるという戦略に立つとしても、もっともな結果に思えます。2位以降のARISEやSLATEも、似たようなものですね。
一方、最悪手は**"UHHUH"**という聞いたこともない単語ですが、残念なことにこちらはWordleの辞書には登録されていないようで、答えとして認められません。
ということで、Wordle内で最悪手の単語はFUZZYということになります。
**「はっきりしない」**というその単語の意味の通り、これを入力してもヒントが与えられる可能性は少なく、答えがはっきりしないままになるわけです。
(オチがつきましたね。よかったよかった。)
……その上にさらに、日本語由来のKUDZU(葛)があるのも、ちょっと日本人としては趣きを感じます。
なぜこんな単語が辞書に載っているのだろうと思ったのですが、どうやら葛は米国では侵略的外来種として増え過ぎてしまい、深刻な環境問題になっているらしいです。ウケる。
UHHUHにしろFUZZYにしろKUDZUにしろ、出現頻度の低い文字から構成されていることに加えて、同じ文字が重なっていると悪手になる、というのは、情報理論など知らなくてもなんとなくわかりそうです。
2手目以降は?
さて、以上では「初手の最善手」を考えるために情報理論を導入したわけですが、実際のところ、このエントロピー戦略は別に初手に限らず、2手目以降も有効だと考えられます。
order_by_entropyに与える単語リストを全単語にするのではなく、ヒントに合致する単語だけに絞っていけばよいだけです。
以下のようなコードで、与えられたヒントから単語のリストを絞ることができます(使い方は後述)。
def make_df(df_char, fixed=dict(), contains=dict(), not_contains=""):
intersection = set(df_char.index)
for key in fixed.keys():
intersection = intersection & set(df_char.index[df_char[key]==fixed[key]])
for key in contains.keys():
intersection = intersection & set(df_char.index[df_char[key]!=contains[key]])
TF_contains = [False]*df_char.shape[0]
for position in {1,2,3,4,5} - set(fixed.keys()) - {key}:
TF_contains = TF_contains|(df_char[position]==contains[key])
intersection = intersection & set(df_char.index[TF_contains])
for char in list(not_contains):
TF_not_contains = [True]*df_char.shape[0]
for position in {1,2,3,4,5} - set(fixed.keys()):
TF_not_contains = TF_not_contains&(df_char[position]!=char)
intersection = intersection & set(df_char.index[TF_not_contains])
return df_char.loc[intersection]
……ただ、新たなヒントが得られるたびに、エントロピーを計算しなおす必要があり、それは流石にチートという気がします。
ですが折角なので、最後までエントロピー戦略を取ることがどれくらい有効なのかを試してみたくなりました。
エントロピー戦略 vs Absurdle ~南海の大決闘~
本家のWordleは一日一回しか解けないので、代わりに激ムズ版WordleであるAbsurdleでエントロピー戦略を試してみます。
Absurdleは、答えの単語が予め決まっておらず、できるだけプレイヤーにヒントを与えないように、毎回答えの単語をこっそり変化させていきます。ずるいですね。
代わりに、本家の6回という制限は取り払われて、無限回文字列を入力できるようになっています。
もはやWordleとは別ゲームなのですが、その難しさはそれはそれで味わい深いので、一度お試しあれ。
実際に自分でやってみると永遠に終わらなくてイライラします。
さて、これまで作った関数を以下のように使えば、ヒントが与えられた状態でのエントロピー戦略を実行できます。
order_by_entropy(
make_df(df_char, fixed={2:"U",5:"Y"}, contains={}, not_contains="RAISECLOTHDMP")
)
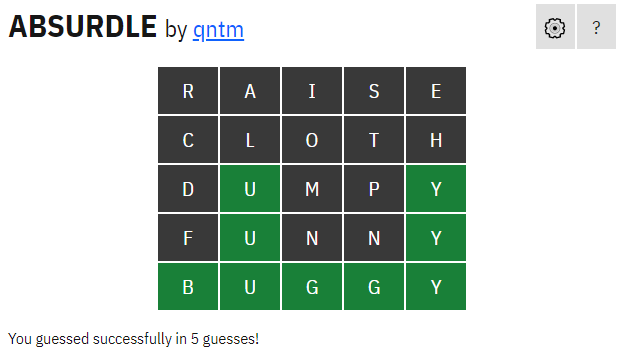
そして、徹頭徹尾エントロピー戦略にAbsurdleに挑んだ結果がこちら。
本家の制限である6手以内の、5手でどうにかクリアすることが出来ました!
親の仇を取ったような気分で感無量です。
……ところが、Absurdleのヘルプには最短4手で終わるとありました。なんと、1手届きません!
まあ、エントロピー戦略は答えの単語がランダムに選ばれることを暗に想定しているのに対し、Absurdleの中身はまったくランダムではありませんので、致し方ありません。
Absurdleを攻略するためには、「Absurdleが動く方向を予め想定して、罠に誘い込む」ような、より高度な戦略が必要なのかもしれません。
もしどなたか攻略法をご存じの方がいらっしゃったら、教えて欲しいところです。
以上。
追記1
Absrudleを4手で攻略した人のTweetを見つけました。
追記2
Gigazineの記事を読んでWordle公式が使ってる正解単語リストの存在を知ったので、再度エントロピー計算をしてみましたが、上位も下位もあまり変わらなかったです。
最下位のMAMMAように一部の単語は手持ちの辞書に意味が乗っていませんでした。もちろんこれは文字通りマンマ、お母さんという意味ですが。
なお、上記の記事によると、最短で解く戦略ではSALETが最適とのこと。
エントロピー戦略2位のSLATEのアナグラムになっていますが、戦略が違うことで微妙に最適な単語が変わるのは面白いですね。
追記3
ヒントが得られた後の手について、もしかしたら助けになるかもしれない記事を書きました。
Wordleのチートシートを作ったよ