この記事に関して
ここでは量子数値積分について量子コンピュータを用いた高速数値積分を参考に説明していきます。
モンテカルロ積分(古典)
古典では乱数を用いた数値積分であるモンテカルロ積分について説明します。
モンテカルロ法は乱数を用いて積分を近似する手法です。
$g$ を $D$ 上可積分関数とすると $(D \subset \mathbb{R}^n)$ 求めたい積分は以下のようになります。
\int_{D}g(x)dx \ , \ g: D \subset \mathbb{R}^n \rightarrow \mathbb{R}
これをモンテカルロ法で求めていきます。
スケーリング
$f$ は $D$ 上可積分関数なので、 $f$ の上界・下界で $K$ 倍してあげると上の積分は以下の形に書き直すことができます。
K\int_{D \subset \mathbb{R}^n}g(x)dx
= \int_{[0,1]^n} \rho(x) h(x) dx \ , \ \rho, h: [0,1]^n \rightarrow [0,1] \\
\left(\int_{[0,1]^n} \rho(x)dx = 1\right)
これで関数と積分範囲を簡単にすることができました。
この積分を区分求積法のように矩形近似すると以下のような近似値 $S(f)$ が得られます。
\int_{[0,1]^n} \rho(x) h(x) dx \approx S(f) = \sum_{x \in J^d}p(x)f(x) \ ,\
J := \{0, 1, \cdots, N-1 \} \\
\left(\sum_{x \in J^d}p(x) = 1 \ , \ f(x) = h\left(\frac{x}{N}\right)\right)
ただしこの方法で数値計算する場合、途方もない時間がかかってしますので
古典では次のような手法で積分計算をします。
モンテカルロ法
ある確率密度関数 $p(x)$ について $g$ の期待値 $E[g(X)]$ は以下のようになります。
E[g(X)] = \int_D g(x)p(x) dx \ , \ p: D \subset \mathbb{R}^n \rightarrow \mathbb{R}
次に以下の式が成り立つような関数 $F_N$ を考えます。
E[F_N(g)] = \int_{D}g(x)dx
この $F$ は $p > 0$ のとき実際に存在して次のように置くことができます。
F_N(g) = \frac{1}{N}\sum_{i=1}^{N}\frac{g(x_i)}{p(x_i)}\ ,
\ x_i \in D
実際に代入すると
E[F_N(g)] = E\left[\frac{1}{N}\sum_{i=1}^{N}\frac{g(X_i)}{p(X_i)}\right]
= \frac{1}{N}\sum_{i=1}^{N}E\left[\frac{g(X_i)}{p(X_i)}\right] \\
= \frac{1}{N}\sum_{i=1}^{N}\int_{D}\frac{g(x)}{p(x)}p(x)dx
= \frac{1}{N}\sum_{i=1}^{N}\int_{D}g(x)dx
= \int_{D \subset \mathbb{R}^n}g(x)dx
成り立つことがわかります。
さらに大数の法則から
F_N(g) \xrightarrow{N \rightarrow \infty} E[F_N(g)]
が成り立つので
\int_{D \subset \mathbb{R}^n}g(x)dx \approx
\frac{1}{N}\sum_{i=1}^{N}\frac{g(x_i)}{p(x_i)}
と積分値を近似的に求めることができます。
通常はこのような方法をとり、これをモンテカルロ法と言います。
量子数値積分
量子では上記のモンテカルロ積分で述べた近似値 $F_N(g)$ ではなく $S(f)$ を求めます。
まずは1次元で $N = 2^n - 1$ として次の値を考えます。
S(f) = \sum_{x=0}^{2^n-1}p(x)f(x)
ここで次の二つの行列 $\mathcal{P}, \mathcal{R}$ を定義します。
\mathcal{P}\left|0\right>_n := \sum_{x=0}^{2^n-1}\sqrt{p(x)}\left|x\right>_n \\
\mathcal{R}\left|x\right>_n\left|0\right>
:= \left|x\right>_n(\sqrt{f(x)}\left|0\right> + \sqrt{1-f(x)}\left|1\right>)
$\mathcal{P}$ は始めの $n$ ビットに作用し、
$\mathcal{R}$ は始めの $n$ ビットの値を $n+1$ ビットに作用させていることがわかります。
これを組み合わせた行列 $\mathcal{A} := \mathcal{R}(\mathcal{P} \otimes \mathcal{I})$ を初期状態 $\left|0\right>_{n+1}$ に作用させると、
\mathcal{A} \left|0\right>_{n+1}
= \sum_{x=0}^{2^n-1}\sqrt{p(x)}\left|x\right>_n\left(\sqrt{f(x)}\left|0\right>
+ \sqrt{1-f(x)}\left|1\right>\right)
これによりビットの係数に $p(x), f(x)$ を入れることができました。
次にこれを $S(f)$ で書き直します。このまま書き直すと式が汚くなるので
以下のベクトル $\left|\Psi_0\right>_{n+1}, \left|\Psi_1\right>_{n+1}$ を導入します。
\left|\Psi_0\right>_{n+1}
:= \sum_{x=0}^{2^n-1}\sqrt{p(x)}\sqrt{\frac{f(x)}{S(f)}}\left|x\right>_n\left|0\right> \\
\left|\Psi_1\right>_{n+1}
:= \sum_{x=0}^{2^n-1}\sqrt{p(x)}\sqrt{\frac{1-f(x)}{1-S(f)}}\left|x\right>_n\left|1\right>
この二つのベクトルを使って書き直すと
\mathcal{A} \left|0\right>_{n+1}
= \sqrt{S(f)}\left|\Psi_0\right>_{n+1} + \sqrt{1-S(f)}\left|\Psi_1\right>_{n+1}
$S(f)$ を作り出すことができました。
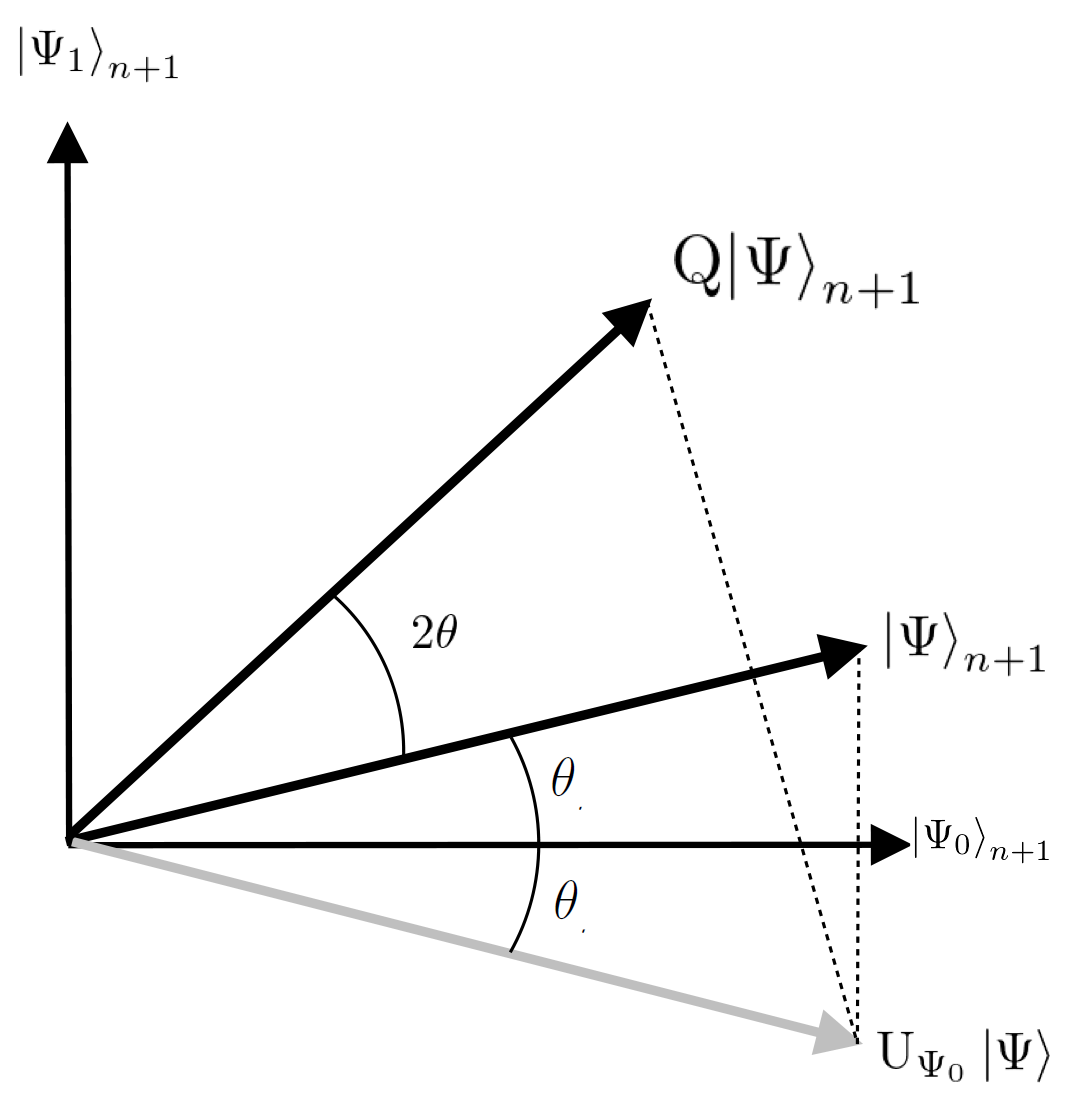
$0 \leq S(f) \leq 1$ より、以下から $\sqrt{S(f)} = \sin\theta$ とします。
最終的に $\theta$ を求めることを目指します。
振幅増幅
振幅増幅の代表的なアルゴリズムとしてグローバーアルゴリズムがあります。
今回はこの一般化である Quantum Amplitude Amplification を参考に振幅増幅行列を説明します。
振幅増幅させる行列 $\mathcal{Q}$ を以下で定義します。
\mathcal{Q} := \mathcal{U}_{\Psi}\mathcal{U}_{\Psi_0}\\
\mathcal{U}_{\Psi_0} := I_n \otimes Z \\
\mathcal{U}_{\Psi} := \mathcal{A}\left(I_{n+1}-2\left|0\right>_{n+1}\left<0\right|_{n+1}\right)\mathcal{A}^{\dagger}
この $\mathcal{Q}$ を $\mathcal{A} \left|0\right>_{n+1}$ に施すと、
\mathcal{Q}^j\mathcal{A} \left|0\right>_{n+1}
= \cos\{(2j+1)\theta\}\left|\Psi_0\right>_{n+1}
+ \sin\{(2j+1)\theta\}\left|\Psi_1\right>_{n+1}
参考:https://en.wikipedia.org/wiki/Grover%27s_algorithm
グローバーのアルゴリズムとの違いは $\theta$ が既知でないことです。
$\mathcal{Q}^j$ に関する証明は @koke-saka さんの 論文解説 を見ていただけるとわかりやすいです。
$\mathcal{Q}$ の固有値と固有ベクトルはここを参考に計算すると
\lambda = e^{\pm 2i\theta} \\
\left|\Psi_{\pm}\right>_{n+1}
= \frac{1}{\sqrt{2}}\left(\left|\Psi_0\right>_{n+1}\mp i\left|\Psi_1\right>_{n+1}\right)
これらから改めて $\mathcal{A} \left|0\right>_{n+1}$ を書き直すと
\mathcal{A} \left|0\right>_{n+1}
= \frac{1}{\sqrt{2}}\left(e^{i\theta}\left|\Psi_+\right>_{n+1} + e^{-i\theta}\left|\Psi_-\right>_{n+1}\right)
何回か $\mathcal{Q}$ を施すことで $\left|\Psi_0\right>$ の振幅が大きくなることがわかります。
(ちなみにグローバーでは $\theta$ が既知なので約 ($\pi/4\theta - 1/2$) 回で振幅が最大になります。)
振幅推定
上で述べた $\mathcal{Q}$ を用いて $\theta$ を取り出すことを考えます。式は $\left|\Psi_{\pm}\right>_{n+1}$ を用いたものを使います。
(通常の量子位相推定についてはここで述べています。)
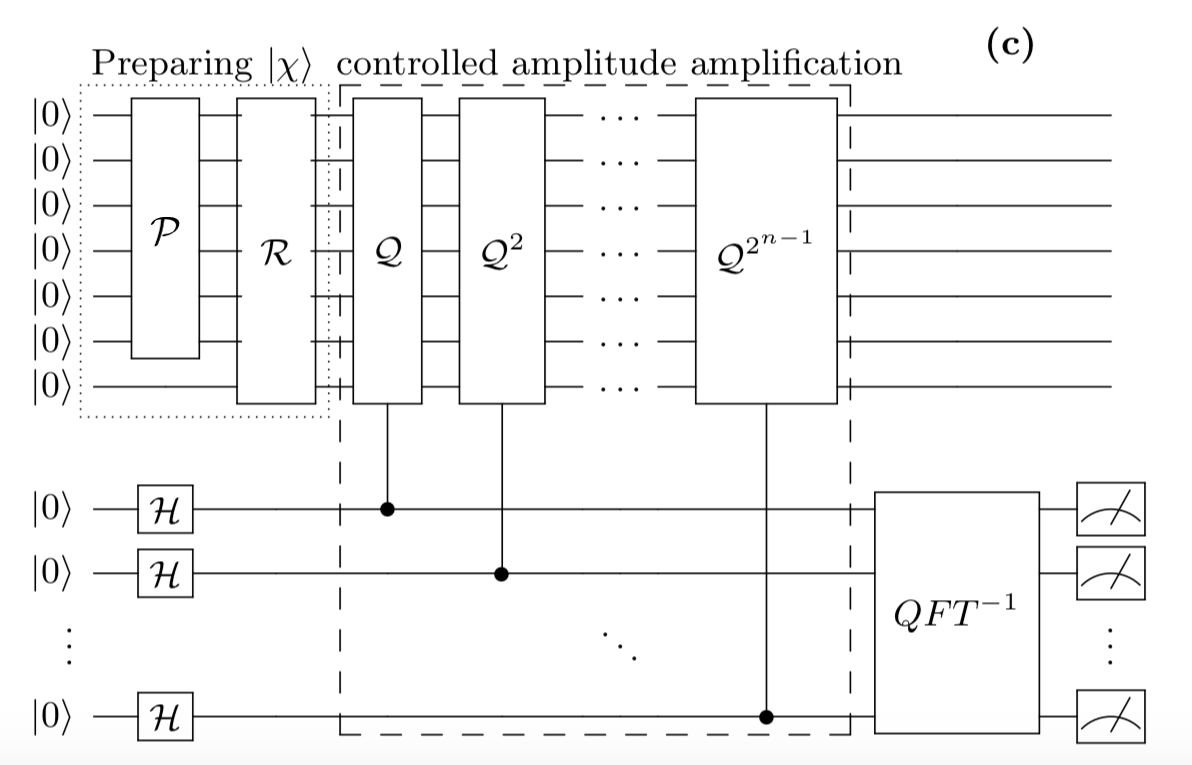
まず $\theta$ を写し出すビットが必要なのでそれを付け足します。
\mathcal{A}\left|0\right>_{n+1} \rightarrow
\left|0\right>_{m}\mathcal{A}\left|0\right>_{n+1}
$m$ ビット付け加えました。これにアダマールゲートを施します。
\left|+\right>_{m}\mathcal{A}\left|0\right>_{n+1}
= \frac{1}{\sqrt{M}}\sum_{x=0}^{M-1}\left|x\right>_m\frac{1}{\sqrt{2}}\left(e^{i\theta}\left|\Psi_+\right>_{n+1} + e^{-i\theta}\left|\Psi_-\right>_{n+1}\right)
ここで $2^m = M$ としています。
次に各 $\left|x\right>_m$ から $\mathcal{A}\left|0\right>_{n+1}$ に制御ユニタリ行列 $\mathcal{CQ}$ を施します。
\mathcal{CQ}\left(\left|+\right>_{m}\mathcal{A}\left|0\right>_{n+1}\right)
= \frac{e^{i\theta}}{\sqrt{2M}}\sum_{x=0}^{M-1}e^{2ix\theta}\left|x\right>_m\left|\Psi_+\right>_{n+1}
+ \frac{e^{i\theta}}{\sqrt{2M}}\sum_{x=0}^{M-1}e^{-2ix\theta}\left|x\right>_m\left|\Psi_-\right>_{n+1}
最後に $\theta$ を求めるために逆量子フーリエ変換 $F_m^{-1}$ を行います。
その前に $\left|S_M(x)\right>$ を新しく定義しておきます。
\left|S_M(x)\right>
:= \frac{1}{\sqrt{M}}\sum_{y=0}^{M-1}e^{2\pi ixy}\left|y\right>\\
\left|S_M(x)\right> = \left|S_M(k+x)\right> \ , \ (k \in \mathbb{Z})
これから $x$ が整数の場合、以下が容易に成り立ちます。
F_m^{-1}\left|S_M\left(\frac{x}{M}\right)\right> = \left|x\right>
よって逆量子フーリエ変換を行うと
\frac{e^{i\theta}}{\sqrt{2}}F_m^{-1}\left|S_M\left(\frac{\theta}{\pi}\right)\right>_m\left|\Psi_+\right>_{n+1}
+ \frac{e^{-i\theta}}{\sqrt{2}}F_m^{-1}\left|S_M\left(1-\frac{\theta}{\pi}\right)\right>_m\left|\Psi_-\right>_{n+1}
ここで $m$ ビットを観測すると $\left|0\right>_m \cdots \left|M-1\right>_m$ のうち
F_m^{-1}\left|S_M\left(\frac{\theta}{\pi}\right)\right>_m
\approx \left|\frac{M}{\pi}\theta\right>_m\ , \
F_m^{-1}\left|S_M\left(1-\frac{\theta}{\pi}\right)\right>_m
\approx \left|M\left(1-\frac{\theta}{\pi}\right)\right>_m
の期待値がもっとも大きくなることがわかります。この観測値について
x \approx \frac{M}{\pi}\theta \ , \ M\left(1-\frac{\theta}{\pi}\right)
とおけば、どちらの値をとっても $\sin\theta$ の性質から
S(f) = \sin^2\theta \approx \sin^2\left(\frac{\pi}{M}x\right)
= \sin^2\left(\pi\left(1-\frac{x}{M}\right)\right)
$\sin\theta$ を近似的に求めることができます。
以上の流れから $S(f)$ を数値積分できることがわかりました。
参考: https://arxiv.org/pdf/1805.00109.pdf
この図から $\mathcal{Q}$ を $M-1$ 回、つまり $\mathcal{A}$ を $2M-1$ 回使用すればいいことがわかります。
d次元
一般の $d$ 次元の場合は $S(f)$ を次のように定義します。
S(f) = \sum_{x_1=0}^{2^n-1}\cdots\sum_{x_d=0}^{2^n-1}p(x_1\cdots x_d)f (x_1\cdots x_d)
またこれに作用させる $\mathcal{P}, \mathcal{R}$ は
\mathcal{P}\left|0\right>_{nd} := \sum_{x_1=0}^{2^n-1}\cdots\sum_{x_d=0}^{2^n-1}\sqrt{p(x_1\cdots x_d)}\left|x_1\right>_n \cdots \left|x_d\right>_n\\
\mathcal{R}\left(\left|x_1\right>_n \cdots \left|x_d\right>_n\left|0\right>\right)
:= \left|x_1\right>_n \cdots \left|x_d\right>_n(\sqrt{f(x_1 \cdots x_d)}\left|0\right> + \sqrt{1-f(x_1 \cdots x_d)}\left|1\right>)
あとは1次元と場合と同様にすれば求められます。
誤差
最後に数値積分で求めた $\theta$ を $\tilde{\theta}$ 、$S(f)$ を $\tilde{S}(f)$ と置き、実際の値との誤差について考えます。
まずは $\theta$ について、通常の絶対値では誤差が測れないので新しく距離 $d$ を定義します。
d\left(\theta, \tilde{\theta}\right)
:= \min_{z \in \mathbb{Z}}\left|z+\tilde{\theta}-\theta\right|
これで $\theta$ と $\tilde{\theta}$ が複素数平面上でどれだけ近いかを表します。
なので
d\left(\theta, \tilde{\theta}\right) = 0 \Leftrightarrow \theta = \tilde{\theta} + l \ , \ l \in \mathbb{Z}\Leftrightarrow e^{2\pi i\theta} = e^{2\pi i\tilde{\theta}}
が成立します。今回はこれを $\theta$ における誤差とします。
この $d$ を用いると適当な自然数 $k>1$ と併せて誤差は以下のようになります。
P\left(d\left(\tilde{\theta}, \theta\right)\le\frac{k}{M}\pi\right)
\ge 1 - \frac{1}{2(k-1)}
また $k=1$ では、最低でも約 $\pi^2/8 \approx 81$ %の確率で誤差が $\pi/M$ 以下になることがわかっています。
次に $S(f)$ に関しては上と同じ $k$ を用いて以下の不等式が成り立ちます。
\left|\tilde{S}(f) - S(f)\right| \le 2\pi k \frac{\sqrt{S(f)(1-S(f))}}{M}
+ k^2\frac{\pi^2}{M^2}
$k$ を見るとわかるように $\theta$ の誤差を小さくなると $S(f)$ の誤差も小さくなります。
まとめ
今回は量子コンピュータを用いた数値積分について説明しました。
次回はこの理論を用いて簡単な例を実装します。
参考文献
宇野 隼平、 量子コンピュータを用いた高速数値積分
https://www.mizuho-ir.co.jp/publication/giho/pdf/010_01.pdf
Patrick Rebentrost, Brajesh Gupt, and Thomas R. Bromley
Quantum computational finance: Monte Carlo pricing of financial derivatives
https://arxiv.org/pdf/1805.00109.pdf
グローバーアルゴリズム
https://qiita.com/KeiichiroHiga/items/99af7f5eae3fbdf7e583
Grover の検索アルゴリズム と Quantum Amplitude Amplification/Estimation
https://whyitsso.net/physics/quantum_mechanics/AA_AE_Grover.html
グローバーのアルゴリズムの一般化 Quantum Amplitude Amplification の論文解説
https://qiita.com/koke-saka/items/16b20edfeca49e1049cd
量子位相推定
https://qiita.com/KeiichiroHiga/items/acee41426809f3ad1257
Gilles Brassard, Peter Høyer, Michele Mosca, Alain Tapp
Quantum Amplitude Amplification and Estimation
https://arxiv.org/pdf/quant-ph/0005055.pdf
Somma Rolando Diego, Xu Guanglei, Daley Andrew, Givi Peyman
Turbulent Mixing Simulation via a Quantum Algorithm
https://www.osti.gov/pages/servlets/purl/1458951