Deep Learning ToolBoxとデータ駆動制御を用いたリカレントニューラルネットワーク型制御器のワンショット学習

はじめに

著者は過去にデータ駆動制御と呼ばれる手法に関する記事を執筆しました。この手法は一組の実験データを用いて，フィードバック制御器をオフラインで自動設計する手法です。繰り返し実験やプラントモデリングを介さずにデータから直接制御器を設計・チューニングできるため，実応用の点で有益な特徴を有する手法です。様々な研究機関・企業で製品応用に関する研究が取り組まれております。

これまでの記事ではPID制御等の線形時不変な制御器をデータからチューニングする事例を紹介してきました。実はあまり知られていないことですが，データ駆動制御は制御器が線形時不変な伝達関数以外でも適用できることがあります。特に，著者が過去に紹介したVirtual reference feedback tuning(VRFT)と呼ばれる方法は制御器の逆モデルを使用しないため，様々な制御器をデータから直接設計できます。例えば，機械学習・データサイエンス分野で用いられているリカレントニューラルネットワーク(RNN)を用いることが考えられます。RNNは非線形システムの時系列応答を模擬可能な手法の一つです。制御器の構造をRNNとして設定し，RNNの重みをVRFTの枠組みで自動設計できれば，複雑な特性を有する未知システムに対する制御器を労力をかけずに設計できるはずです。

以上の背景のもと，本記事ではRNN型制御器をデータ駆動制御にてワンショットチューニングする手法に関して説明いたします。数値例を用いて，一組の実験データのみを用いて制御器を自動設計できるかを検証します。なお，本記事ではMATLABのDeep Learning Toolboxを用いた数値例をご紹介しますが，Pythonのライブラリを用いても特に問題ありませんので，ご興味あればお試しいただければ幸いです。

なお，本記事執筆にあたり下記の文献を大変参考にさせていただきましたので、文献情報を記載させていただきます。オープンアクセスのため，こちらも読んでいただくと理解が深まるかもしれません。

参考文献
Wakasa, Y., Nakatani, K., Murakami, S., & Adachi, R. (2021). Data-driven tunig of LSTM controllers for systems with nonlinearities. ICIC Express Letters, 15(5), 421-427.

問題設定

本記事で紹介する制御系設計の目的に関して簡単に述べておきます。ここでは，制御対象として未知の時変システム：

y(k)=f(x(k),u(k))

を考えます。本システムでは$y(k)$が出力，$u(k)$が制御入力，$x(k)$が時変パラメータとします。この制御対象の出力$y(k)$を目標値$r(k)$に近づけることを考えます。具体的には，規範モデル$T_{d}$を線形時不変な伝達関数としてあらかじめ与えます。$T_{d}$は閉ループ系の要求仕様を伝達関数として定量化したものだと考えてください。上記の時変システムを対象とする閉ループ系を規範モデル$T_{d}$に一致させるフィードバック制御器を導出することを目指します。ただし，本システムは$x(k)$に依存する時変システムのため，PID制御器のような線形時不変の制御器では所望の制御応答達成が望めません。さらに，制御対象の特性が未知のため，プラントモデルに基づく制御系設計アプローチを採用できません。以上の点から，制御対象の操業データのみを用いて，時変システムに対応可能な非線形なフィードバック制御器をデータから直接設計することを目指します。

Fig.1 制御系のブロック線図

VRFTの概要

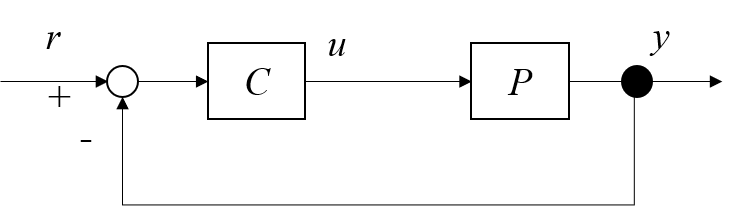
ここではVRFTの概要を述べておきます。Fig.2の線形時不変システムにおけるフィードバック制御系を考えます。Fig.2の$P$は線形時不変な制御対象となります。$T_{d}$は閉ループ系の要求仕様を伝達関数として定量化したものだと考えてください。VRFTではFig.2の閉ループ伝達関数を規範モデル$T_{d}$に一致させる線形時不変な制御器$C$を導出することを目指します。

Fig.2 SISOの制御系

まず，開ループ/閉ループ実験のどちらかで制御対象の初期入出力データ(時系列データ)を取得します。次に，初期入出力データを用いて擬似誤差信号$e_{s}$と整形後制御入力$u_{s}$を

u_{s}(k)=L u_{0}(k)

e_{s}(k)=L\left(\frac{1}{T_{d}} y_{0}(k)-y_{0}(k)\right)

と導出します。$u_{0}$と$y_{0}$は初期実験で取得した入出力応答の時系列データです。$L$はノイズ除去やノンプロパーな伝達関数計算を回避するためのプレフィルタです。プレフィルタの設計に関しては後ほど解説します。上記の信号を用いて，VRFTの評価関数を

J_{VRFT}(C)=\sum_{k=1}^{N} \left(u_{s}(k)-C e_{s}(k)\right)

と定義します。$N$が時系列データのデータ点数です。この評価関数は制御器$C$でパラメタライズされています(厳密な表記ではありませんが，わかりやすさ重視でこのような表記をしています)。何らかの数理最適化手法にて評価関数$J_{VRFT}$を最小化するような制御器$C$のパラメータを探索します。例えば，制御器$C$が評価関数に対して線形関数になれば最小二乗法にて評価関数を最小化できます。評価関数を十分小さくできれば，規範モデルと閉ループ伝達関数を一致させるような制御器$C$を導出できます。VRFTによる制御器更新手順は下記のようにまとめることができます。

1.プレフィルタ$L$と規範モデル$T_{d}$をあらかじめ与える。
2.開ループ/閉ループ実験のどちらかで入出力応答を測定する。
3.$J_{VRFT}$を最小化する制御器$C$のパラメータを数理最適化にて導出する。

VRFTは一組の実験データを測定するだけで未知システムに対する制御器をオートチューニングできます。制御器$C$がPID制御器であれば，最小二乗法にてPIDゲインを導出できます。つまり，最適化における計算コストが非常に低く，パラメータの最適性が保証されます。

※ VRFTのより詳細な説明に関しては過去記事をご参照ください。Pythonのサンプルコードも記載しております。別記事として，MATLAB版のサンプルコードも公開しております。

※ VRFTの詳細な説明は拙著としてkindleで教科書を出版しております。タイトルは「職場で使えるデータ駆動型PIDオートチューニング入門 : FRITとVRFT編」です。こちらもお読みいただければ、より理解が深まるかもしれません。

VRFTによるRNN型フィードバック制御器

前節で紹介したVRFTは線形時不変システム向けの制御系設計手法でした。本章では，VRFTを時変システムの制御系に拡張することにより，未知の時変システムに対応したフィードバック制御器を操業データからオフラインで獲得することを目指します。なお，本記事ではRNNやLSTMにおける詳細な説明は紙面の都合で省略します。もしRNNやLSTMの原理や構造に関して深く理解したい方がいらっしゃれば，下記の記事等をご参照いただければと思います。

RNN型フィードバック制御器

RNNとは過去の時刻の情報を用いて現時刻および将来の入力に対するネットワーク性能を向上させる，ニューラルネットワーク構造です。今回はRNNの中でも時系列データの学習や予測に適したLSTMを採用します。LSTM 型のRNNは時系列応答データに含まれる長期の関係を，ネットワークがより効果的に学習できることが特徴の方法です。本来の用途としては非線形・時変な制御対象のプラントモデリングに活用されることが多い手法となります。ただし，今回の目的はプラントモデリングをスキップしてデータから直接フィードバック制御器を設計することです。したがって，LSTM 型のRNNをフィードバック制御器の構造として与えることにより，時変システムに対して所望の制御応答を実現可能なフィードバック制御器設計を目指します。

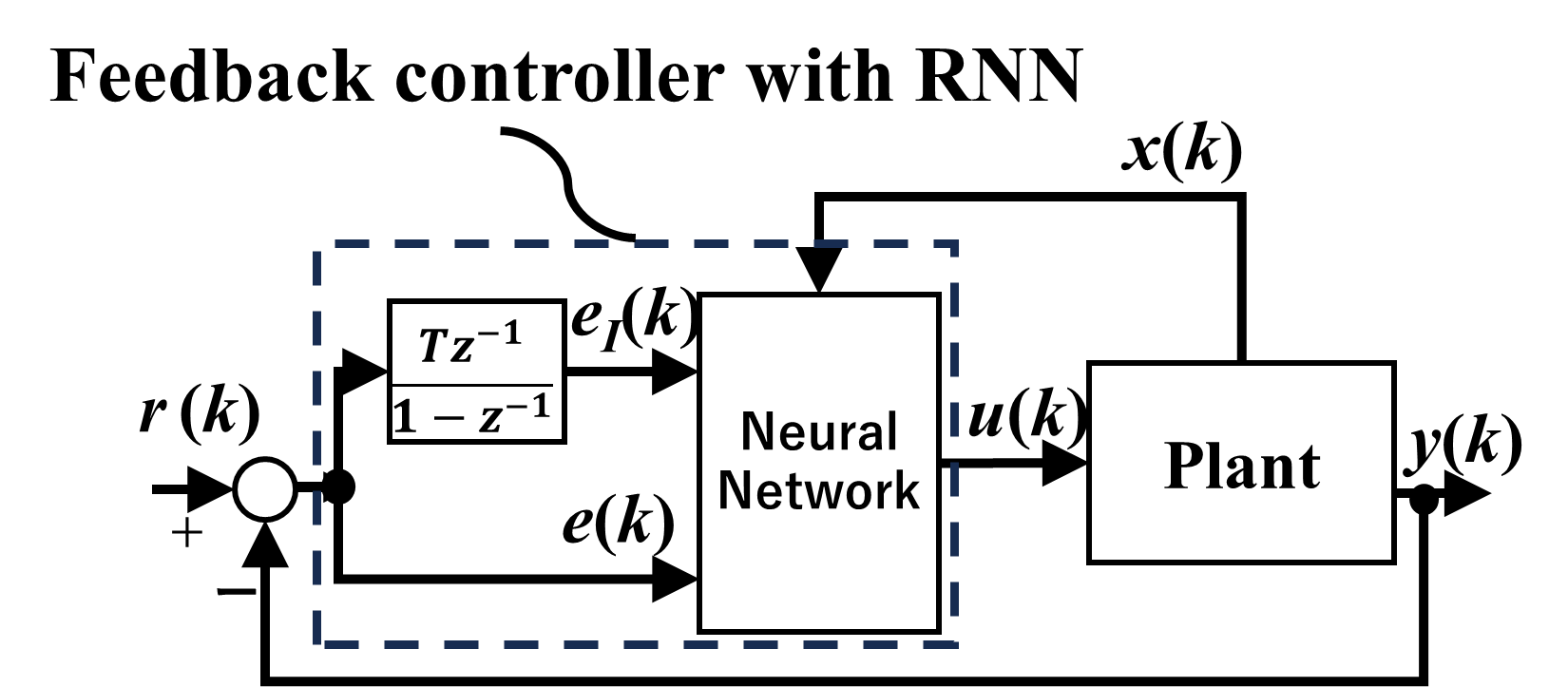
LSTMを用いたフィードバック制御系をFig.3に示します。本制御系ではフィードバック制御器の構造を3入力・1出力のLSTM型RNNとして設定します。RNNのレイヤー数はユーザーが事前設定するものとします。目標値と出力の偏差$e(k)$，偏差の積分値$e_{I}(k)$，時変パラメータ$x(k)$を入力することにより，RNNが制御入力$u(k)$を計算して制御対象へ入力します。制御対象によっては内部モデル原理的に必ずしも積分器が必要となるわけではありませんが，今回は誤差の積分値もRNNの入力として設定しております。LSTM型のRNNは隠れ状態のレイヤーにおけるベクトル用と入力用の二種類の重みを調整する必要があります。本制御系では所望の制御応答を実現するため，実際の閉ループ系の応答と規範モデル$T_{d}$が一致するようにRNNの重みを調整しなければなりません。そこで，次節ではVRFTを用いてRNNの重みを自動調整する手法に関して解説していきます。

(a) 制御系のブロック線図

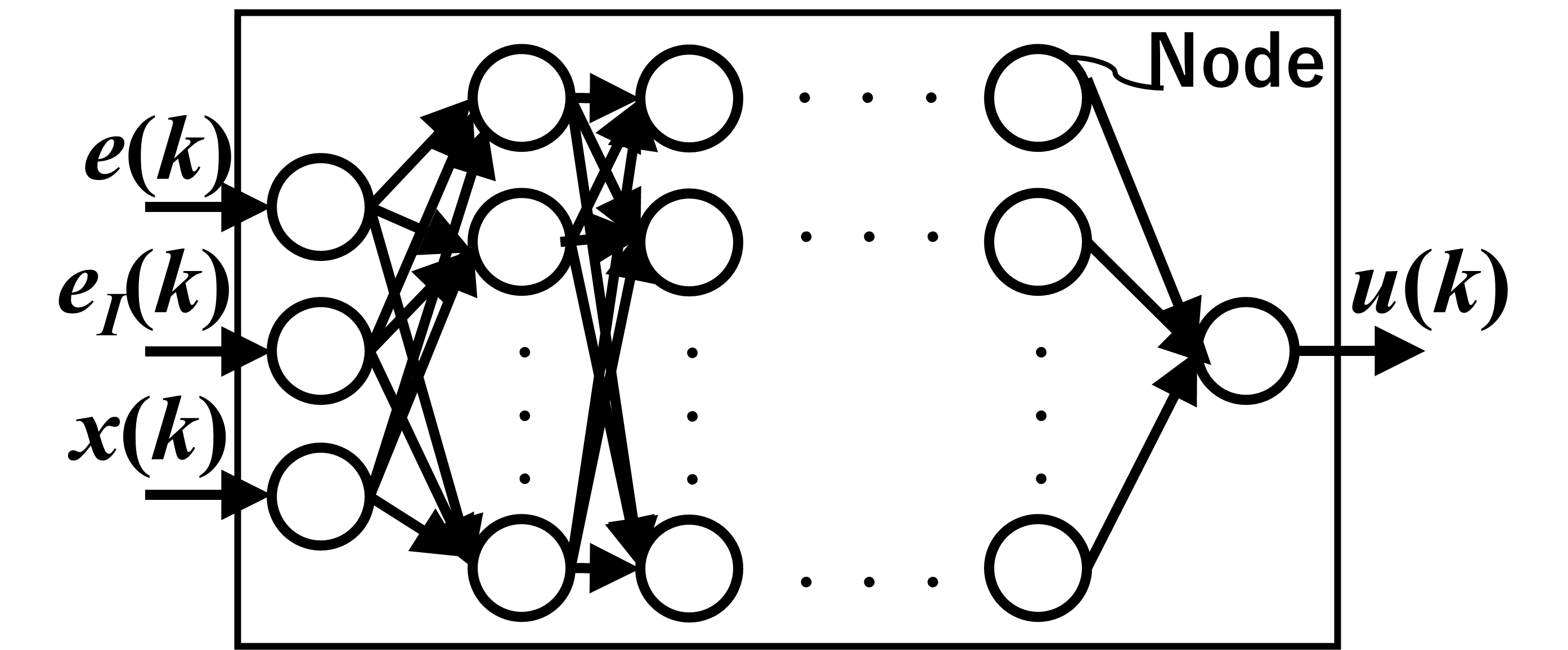
(b) RNNの構成
Fig.3 LSTM 型のRNNを用いた時変システムのフィードバック制御系

VRFTの適用

Fig.3におけるRNNの重みを一組の実験データのみを用いてオフライン調整する方法を解説します。まず，初期実験として開ループ/閉ループ実験のどちらかで制御対象の入出力と時変パラメータの有限時系列データを取得します。初期実験における$u$の有限時系列データを$u_{0}$，$y$の有限時系列データを$y_{0}$,$x$の有限時系列データを$x_{0}$とします。

次に，入出力データを用いて擬似誤差信号$e_{s}$と整形後制御入力$u_{s}$を

u_{s}(k)=L u_{0}(k)

e_{s}(k)=L\left(\frac{1}{T_{d}} y_{0}(k)-y_{0}(k)\right)

と導出します。$L$はノイズ除去やノンプロパーな伝達関数計算を回避するためのプレフィルタです。擬似誤差信号$e_{s}$の積分値($e_{s}$を積分器に入力した際に得られる出力値)を$e_{sI}$とします。ここで，$e(k)$と$e_{I}(k)$と$x(k)$の代わりに，$e_{s}(k)$と$e_{sI}(k)$と$x_{0}(k)$をFig.3のRNNに入力することを考えます。その場合に得られるRNNの出力$u_{RNN}(k,\theta)$を

u_{RNN}(k,\theta):=f_{RNN}(e_{s}(k),e_{sI}(k),x_{0}(k),\theta)

と定義します。$f_{RNN}$がRNNの関数であり，$\theta$はRNNの重み係数となります。上記の信号を用いて，VRFTの評価関数を

J_{RNN}(\theta)=\sum_{k=1}^{N} \left(u_{s}(k)-u_{RNN}(k,\theta)\right)

と定義します。この評価関数はRNNの重み係数$\theta$でパラメタライズされています。何らかの数理最適化手法にて評価関数$J_{RNN}$を最小化するようなRNNの重み$\theta$を探索します。評価関数を十分小さくできれば，規範モデルの応答と制御応答を一致させるようなRNN型フィードバック制御器を導出できます。VRFTによる制御器調整手順は下記のようにまとめることができます。

1.プレフィルタ$L$と規範モデル$T_{d}$をあらかじめ与える。
2.初期実験にて$u$の有限時系列データを$u_{0}$，$y$の有限時系列データ$y_{0}$,$x$の有限時系列データ$x_{0}$を測定する。
3.$J_{RNN}$を最小化するRNNの重み$\theta$を数理最適化にて導出する。

本手順により，VRFTにてFig.3の制御系におけるRNNの重みを一度の実験のみでオートチューニングできます。

数値例

それでは例題を通して、VRFTとRNNを用いて時変システムの制御器をデータから自動設計してみましょう。簡単な例として次の対象に対する制御系設計問題を考えてみます。制御対象を

\frac{dy}{dt}=-\frac{1}{Tx}y+\frac{K}{T} u

と設定します。参照モデルの伝達関数を

T_d=\frac{1}{0.35s+1}

とします。この対象に対して，一般的なPI制御器：

C=K_{P}+\frac{K_{I}}{s}

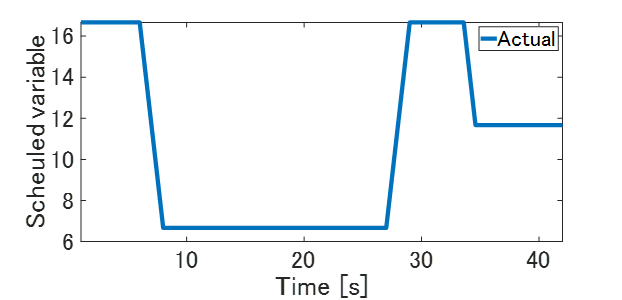
を適用してみます。これらの関数は連続系で記載していますが，数値シミュレーションにあたり離散化を施しています。本システムではスケジュールパラメータ$x$がFig.4のように時間変化するとします。上記のPID制御器$C$を使った閉ループ実験にて制御対象の実験データ測定してみましょう。

Fig.4 時変パラメータの挙動

まず、閉ループ応答データを測定します。目標値信号に関しては，制御応答の連続的な挙動がわかりやすいようにランプとステップを混ぜたような信号とします。PID制御器を使った閉ループ実験にて、入出力応答を測定します。Fig.5が実験時の閉ループ応答です。PIDゲインの値が適当なこともありますが、制御対象が時変系のシステムのためPID制御では所望の制御応答を実現できていません。

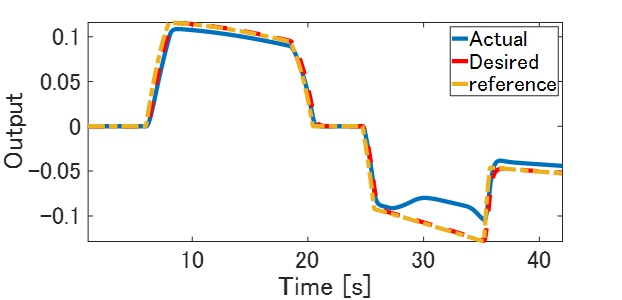
(a) 出力

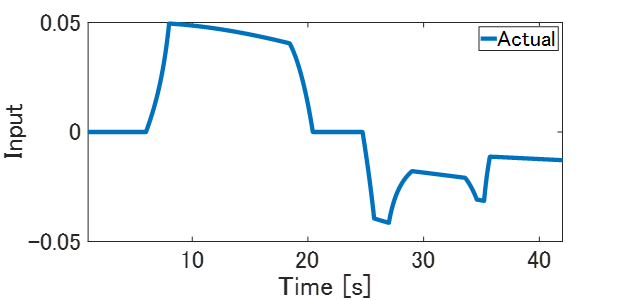
(b) 入力
Fig.5 PID制御による制御結果

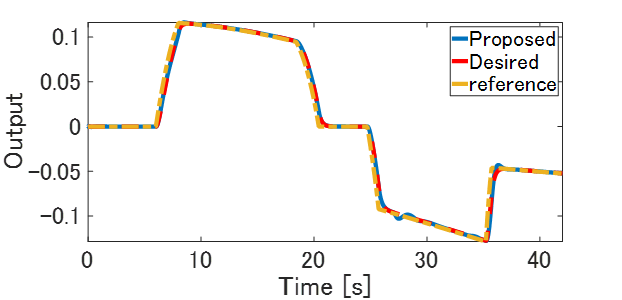
この時系列データを使ってLSTM型のRNN制御器を設計します。ここでは、Deep Learning ToolboxのtrainNetwork関数を用います。最適化アルゴリズムはADAMアルゴリズムを適用します。LSTMのレイヤー数は5としました。一組の実験データのみを用いてオフライン学習させたRNN型制御器を実装し，再度数値シミュレーションしました。Fig.6が再シミュレーンの結果です。制御応答が参照モデルの応答に近づいていることがわかります。制御対象が時変系の場合でも，VRFTの枠組みでLSTM型のRNN制御器をオフラインチューニングすることで所望の制御応答を実現できています。以上の結果から，VRFTを拡張することで所望の制御系を自動設計できることを確認できました。

Fig.6 制御結果

おわりに

本記事では，VRFTと呼ばれる一度実験するだけで所望の制御器を自動獲得可能なオートチューニング手法の拡張に関して解説しました。VRFTには色々なメリットがあり，今回のような制御器設計にも活用できます。もし興味があれば皆様の研究・業務で実際に活用してみてください。

サンプルコード

数値例にて使用したサンプルコードです。MATLAB, Control system Toolbox, DeepLearning Toolboxがあれば使用できます。

%yが出力データ、uが制御入力データ、xが時変パラメータ
L=Td;%プレフィルタ
intg=tf(1,[1,0]);

d=lsim(L,u,t);
eth=lsim(L*(1-Td)/Td,y,t);
eth_intg=lsim(intg,eth,t);
ref=[t',ref];

xdata = [eth,eth_intg,x]';
ydata = d';
% レイヤ定義
layers = [sequenceInputLayer(3);
    lstmLayer(5);
    fullyConnectedLayer(1);
    regressionLayer()];
% 学習オプション / 学習
opts = trainingOptions('adam','InitialLearnRate',1e-2,MaxEpochs=10000);
net = trainNetwork(xdata, ydata, layers, opts);