はじめに
国内の制御界隈では,データ駆動制御と呼ばれる手法が普及しつつあります。その中でも,FRITと呼ばれる手法は一度実験するだけで所望の制御器を自動獲得可能なオートチューニング手法です。実応用上優れた特性を有しているため,様々な企業・大学で注目されている技術といえます。一方,FRIT関連の論文を読むと,Virtual reference feedback tuning(VRFT)と呼ばれる手法が先行研究として挙げられています。VRFTも一度実験するだけで所望の制御器を自動獲得可能なオートチューニング手法です。FRITとVRFTは非常に類似した手法ですが,一体何が違うのでしょうか? 実はVRFTにはFRITよりも優れた特徴がいくつかあります。
本記事ではVRFTを解説していきます。また,この記事を読んだ読者が実践できるようにサンプルプログラムも付録に載せておきます。
※ MATLAB版のサンプルコードも公開しました。
※ 本記事をもとに加筆・修正を加えた入門書をkindleで出版しました。タイトルは「職場で使えるデータ駆動型PIDオートチューニング入門 : FRITとVRFT編」です。こちらもお読みいただければ、より理解が深まるかもしれません。
VRFTの概要
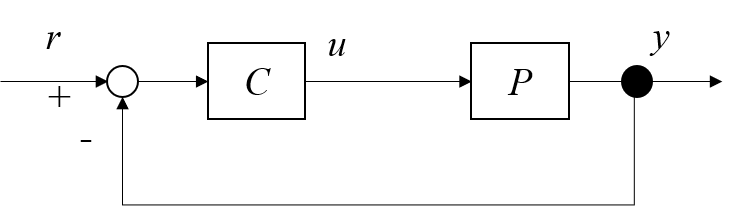
ここではVRFTの概要を述べておきます。Fig.1のフィードバック制御系を考えます。オートチューニングの前提として,規範モデル$T_{d}$をあらかじめ与えます。$T_{d}$は閉ループ系の要求仕様を伝達関数として定量化したものだと考えてください。VRFTではFig.1の閉ループ伝達関数を規範モデル$T_{d}$に一致させる制御器$C$を導出することを目指します。
まず,開ループ/閉ループ実験のどちらかで制御対象の初期入出力データ(時系列データ)を取得します。次に,初期入出力データを用いて擬似誤差信号$e_{s}$と整形後制御入力$u_{s}$を
u_{s}=L u_{0}
e_{s}=L\left(\frac{1}{T_{d}} y_{0}-y_{0}\right)
と導出します。$u_{0}$と$y_{0}$は初期実験で取得した入出力応答の時系列データです。$L$はノイズ除去やノンプロパーな伝達関数計算を回避するためのプレフィルタです。プレフィルタの設計に関しては後ほど解説します。上記の信号を用いて,VRFTの評価関数を
J_{VRFT}(C)=\left\|u_{s}-C e_{s}\right\|^{2}
と定義します。この評価関数は制御器$C$でパラメタライズされています(厳密な表記ではありませんが,わかりやすさ重視でこのような表記をしています)。何らかの数理最適化手法にて評価関数$J_{VRFT}$を最小化するような制御器$C$のパラメータを探索します。例えば,制御器$C$が評価関数に対して線形関数になれば最小二乗法にて評価関数を最小化できます。評価関数を十分小さくできれば,規範モデルと閉ループ伝達関数を一致させるような制御器$C$を導出できます。VRFTによる制御器更新手順は下記のようにまとめることができます。
1.プレフィルタ$L$と規範モデル$T_{d}$をあらかじめ与える。
2.開ループ/閉ループ実験のどちらかで入出力応答を測定する。
3.$J_{VRFT}$を最小化する制御器$C$のパラメータを数理最適化にて導出する。
VRFTは一組の実験データを測定するだけで未知システムに対する制御器をオートチューニングできます。制御器$C$がPID制御器であれば,最小二乗法にてPIDゲインを導出できます。つまり,最適化における計算コストが非常に低く,パラメータの最適性が保証されます。FRITでは制御器$C$がPID制御器だと非線形最適化による制御器パラメータ調整しかできず,パラメータの最適性も保証されません。PIDゲインを最小二乗法で求解できる点は,VRFTの強い利点と言ってもいいでしょう。
まったくの余談ですが,VRFTは制御理論のトップジャーナルである「Automatica」で発表された手法です。その後の続報もIEEE Transactions on Automatic Control等のトップジャーナルやその他中堅ジャーナルに多数掲載されており,実は海外ではVRFTの方が有名な手法です。
参考文献
Campi, M. C., Lecchini, A., & Savaresi, S. M. (2002). Virtual reference feedback tuning: a direct method for the design of feedback controllers. Automatica, 38(8), 1337-1346.
VRFTに関するいくつかの誤解
個人的見解ですが,VRFTは色々な観点からFRITよりも優れた特性を有していると感じております。ただし,国内ではVRFTに対するいくつかの誤解もあって,あまりVRFTを活用している人がいなさそうです。本章では,VRFTに関するいくつかの誤解に関して私なりの考察を述べます。
VRFTは開ループ実験データ推奨って本当?
FRITの論文のいくつかでは,「FRITは閉ループ実験データで制御器調整できるのに対して,VRFTは開ループ実験データが推奨されている」と説明されていることがあります。この説明だけ読むと,VRFTは閉ループ実験データを用いた制御器チューニングに不向きな印象をうけます。しかし,実際にはそのようなことはなく,閉ループ実験データを用いてもVRFTにて制御器チューニングできます。なぜVRFTは「開ループ実験データ推奨」と呼ばれているのでしょうか? その理由をVRFTの評価関数から考察していきましょう。
式変形は割愛しますが,初期実験データに含まれるノイズや外乱が十分小さいケースでは上記のVRFTの評価関数は
J_{VRFT}(C)=\left\|\left\{C_{d}-C\right\} u_{e} \right\|^{2}
T_{d}=\frac{PC_{d}}{1+PC_{d}}
u_{e}=\frac{L}{C_{d}}u_{0}
と等価変換できることが知られています。$C_{d}$とは閉ループ伝達関数を規範モデルと一致させる理想的な制御器です。上記の評価関数は,入力$u_{e}$に対する理想制御と制御器間の出力の誤差を評価することを意味します。システム同定の知見を有する方であればピンとくるかもしれませんが,この式はVRFTにおける最適化が「$C_{d}$を制御対象・ノミナルモデルを制御器$C$とみなしたとき,同定入力$u_{e}$を印加して理想制御器$C_{d}$を制御器$C$としてシステム同定する」に相当することを意味します。いいかえると,$u_{e}$がPEであれば,$J_{VRFT}=0$のときに$C_{d}=C$となることが保証されます。これがVRFTの制御器パラメータ調整の裏に隠れた原理です。
システム同定であれば,よいモデルを得るには制御対象を励起するような同定入力を印加する必要がありました。それと同じく$C$と$C_{d}$が十分一致するようなパラメータ調整を実現する場合,$u_{e}$が理想制御器を励起するような信号である必要があります。開ループ実験にて$u_{0}$をM系列信号やパルス信号として設定すれば,$u_{e}$が幅広い周波数成分を含む信号になり,ほとんどの構造の制御器を調整できるようになります。これが「VRFTは開ループ実験推奨である」といわれる理由の一つであると思われます。
ただし,実用上は$u_{0}$をM系列信号やパルス信号に設定しなくても,良好な制御器パラメータ調整を実現できることがほとんどです。低次の伝達関数を励起する場合は同定入力が幅広い周波数成分を有する必要がないからです。これもシステム同定の知見を有する方であればピンとくるかもしれません。例えば,一次遅れ系を励起する場合は単一周波数成分の正弦波を入力すればよいだけです。二次遅れ系であれば,二つの周波数成分の合成波を印加すれば対象を励起できます。つまり,理想制御器がよほど高次の伝達関数でない限りは,$u_{0}$がM系列信号やパルス信号でなくとも,ほとんどのケースにて理想制御器の伝達関数を励起できるということです。PID制御器程度の次数であれば,閉ループ実験/開ループ実験データのどちらを使ってもほとんど変わらないパラメータになると思います。
ここまでの議論をまとめると,下記のようになります。
(1).
VRFTは「$C_{d}$を制御対象・ノミナルモデルを制御器$C$とみなしたとき,同定入力$u_{e}$を印加して理想制御器$C_{d}$を制御器$C$としてシステム同定する」ことに相当。
(2).
開ループ実験にて$u_{0}$をM系列信号やパルス信号として設定すれば,ほとんどのケースにて$u_{e}$が理想制御器を十分励起するような信号になり,どのような制御器のパラメータも調整可能。
(3).
ただし,制御器がよほど高次の伝達関数でない限りは,閉ループ実験/開ループ実験データのどちらを使ってもパラメータ調整結果はほぼかわらない。
※ ここまでの議論は初期実験データに含まれるノイズや外乱が十分小さいという前提に基づいています。
※ 実際には制御対象に対するPE性も影響してくるので,厳密な考察ではないことに注意してください。
以上の理由から,閉ループ実験データを用いて制御器パラメータ調整しても特に問題ないといえるでしょう。なお,今回は評価関数の形に基づく定性的な考察をしましたが,実はパーセバルの定理を使えばより納得のいく考察をすることもできます。このあたりは要望あれば次回以降解説したいと思います。
VRFTのプレフィルタ設計ってどうやるの?
VRFTでは,ノンプロパーな伝達関数計算の回避やノイズ除去の理由でプレフィルタを設計する必要があります。プレフィルタ設計問題もVRFTの課題として言及されることがあります。実際どのようにプレフィルタを設計すればよいのでしょうか?
実はVRFTの先行研究では,下記のようにプレフィルタを設計することが提案されています。
L=T_{d}
これはもっともシンプルな方法でして,プレフィルタを規範モデルとして設定しただけです。厳密な意味での最適性は保証されませんが,VRFTを実システムに応用する場合はほとんどのケースで問題ないことが述べられています。この手法を使えば,ユーザーがプレフィルタを設計する必要は特にありません。後述の検証でもこのプレフィルタを適用しても特に問題がないことを確認しております。プレフィルタ設計も実応用上はほとんど問題にならないと言ってもよいでしょう。
参考文献
Formentin, S., Savaresi, S. M., & Del Re, L. (2012). Non-iterative direct data-driven controller tuning for multivariable systems: theory and application. IET control theory & applications, 6(9), 1250-1257.
Yahagi, S., & Kajiwara, I. (2021). Direct tuning of gain-scheduled controller for electro-pneumatic clutch position control. Advances in Mechanical Engineering, 13(8), 16878140211036017.
VRFTによるPID調整ツール
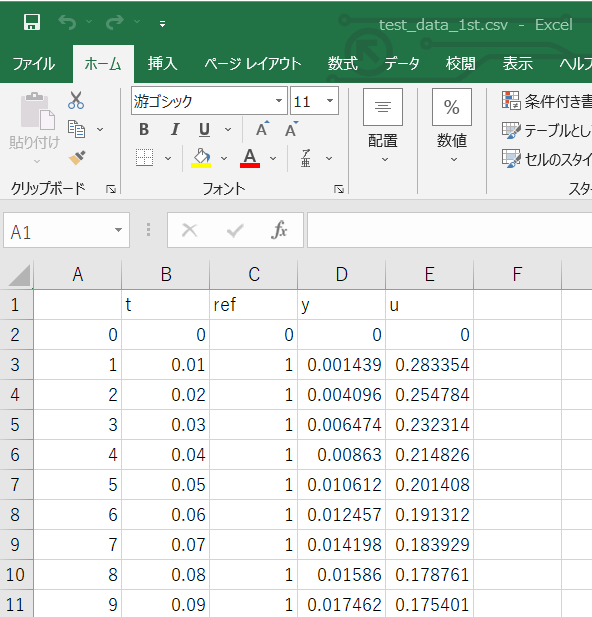
それではVRFTを使ったPID制御器調整のデモをしてみましょう。Pythonを使ったツールを作成し,VRFTの動作を確認していきます。実際の実験を想定し,CSVファイルから入出力データを読み込みこんで制御器を調整します。詳細は付録サンプルコードを参照してください。
例題1:一次遅れ系
まず,簡単な例として一次遅れ系の制御対象に対するPID制御器調整問題を考えてみましょう。制御対象の伝達関数を
P=\frac{1}{s+1}
と設定します。また,制御器を一般的なPID制御器:
C=K_{P}+\frac{K_{I}}{s}+\frac{K_{D}s}{0.05s+1}
としました。本例題では,PIDゲインの初期値は$K_{P}=0.1$,$K_{I}=0.5$,$K_{D}=0.01$と設定しました。最後に,規範モデルを
T_{d}=\frac{1}{0.5s+1}
と与えました。以上の問題設定のもと,VRFTを使ってPIDゲインを調整することを目指しましょう。
まず,閉ループ応答データを測定します。初期のPIDゲインを使った閉ループ実験にて,入出力応答を測定します。Fig.2が初期実験時の閉ループ応答です。出力が規範モデルの目標値応答と一致していないことがわかります。したがって,出力と規範モデルの応答が一致するようにPIDゲインを調整しないといけません。
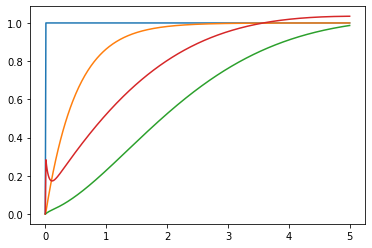
Fig.2 初期データ(青:目標値、橙:規範モデルの目標値応答、緑:出力、赤:制御入力)
この閉ループ応答データを用いて,VRFTにてPIDゲインを調整してみましょう。2章で紹介したプレフィルタを導入し,最小二乗法にてVRFTの評価関数を最小化しました。その結果,PIDゲインの値をそれぞれ,$K_{P}= 2.00$, $K_{I}= 2.00$, $K_{D}= 0.0$と得ることができました(実際には計算されたゲインに対して,有効数字で切り捨て・切り上げしています)。制御器調整後の閉ループ実験結果が下記のFig.3になります。出力が規範モデルの応答と重なっており,望ましい制御器調整を実現できています。本結果から,閉ループ実験データを使ってもPID制御器をオートチューニングできることがわかります。
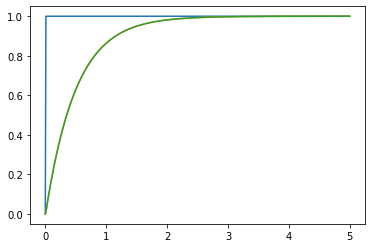
Fig.3 調整後データ(青:目標値、橙:規範モデルの目標値応答、緑:出力)
例題2:二次遅れ系
次に,二次遅れ系の制御対象に対するPID制御器調整問題を考えてみましょう。制御対象の伝達関数を
P=\frac{1}{s^2+2s+1}
と設定します。それ以外の条件設定は例題1と同じです。初期PIDゲインを用いた閉ループ応答が下記のFig.4になります。出力が規範モデルの目標値応答と一致していないことがわかります。したがって,出力と規範モデルの応答が一致するようにPIDゲインを調整しないといけません。
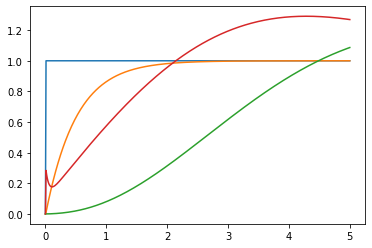
Fig.4 初期データ(青:目標値、橙:規範モデルの目標値応答、緑:出力、赤:制御入力)
この閉ループ実験データを用いて,VRFTにてPIDゲインを調整してみましょう。2章で紹介したプレフィルタを導入し,最小二乗法にてVRFTの評価関数を最小化しました。その結果,PIDゲインの値をそれぞれ,$K_{P}= 3.80$, $K_{I}= 2.07$, $K_{D}= 2.21$と得ることができました。制御器調整後の閉ループ実験結果が下記のFig.5になります。初期閉ループ実験と比べると出力が規範モデルの応答に近づいており,望ましい制御器調整を実現できています。本結果から,二次遅れ系に対してもPID制御器をオートチューニングできることがわかります。
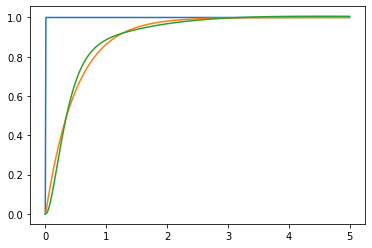
Fig.5 調整後データ(青:目標値、橙:規範モデルの目標値応答、緑:出力)
この結果を見た方は「どうして二次遅れ系では完全に目標値応答と出力が一致してないの?」と疑問に思うかもしれません。これはモデルマッチング誤差の影響を受けているためであり,FRITにも共通して起こりうる現象です。今回の例題における問題設定では,PID制御器のパラメトリゼーションの中で規範モデルと実際の閉ループ伝達関数を一致させるパラメータがないため,出力と目標値応答を完全に一致させることができないのです。もう少しかみ砕いて説明するのであれば,「どのような方法でPID制御器を限界までチューニングしても,PID制御器の構造では原理的に目標値応答を達成できない」ということになります。もし出力と目標値応答を完全に一致させたいのであれば,制御器をより複雑なものに変更/規範モデルを変更する,のどちらかの手順が必要となります。モデルマッチング誤差の影響に関する詳細な分析に関しては,下記の参考文献を載せておきます。気になる方がいればぜひチェックしてみてください。
参考文献
梶原諒太, 増田士朗, & 松井義弘. (2018). 閉ループステップ応答データを用いた FRIT における最適プレフィルタ設計. 計測自動制御学会論文集, 54(2), 238-246.
松井義弘, 綾野秀樹, 増田士朗, & 中野和司. (2017). FIR フィルタによる VRFT のためのプレフィルタの実現. 電気学会論文誌 C (電子・情報・システム部門誌), 137(7), 884-890.
おわりに
本記事では,VRFTと呼ばれる一度実験するだけで所望の制御器を自動獲得可能なオートチューニング手法を解説しました。VRFTには色々なメリットがあり,FRITよりも優れた部分もたくさんあります。もし興味があれば皆様の研究・業務で実際に活用してみてください。また,今回は簡単なPID制御器調整の説明のみでしたが,最新の研究ではVRFTやFRITを使ってゲインスケジュールドPIDのような非線形制御器をオートチューニングする方法も提案されています。もしご要望あればこちらも解説していこうと思います。
サンプルコード
付録にサンプルコードを載せておきます。使い方としては,制御器調整に使う実験データを下記の図の要領でCSVファイルとして用意するだけです。PI制御器とPID制御のどちらかを選んで制御器調整できます。
# データ駆動制御プログラム:PID調整
# 作成日2022/11/19(自称AI・制御エンジニア)
# 更新日2022/11/19(自称AI・制御エンジニア)
import numpy as np
from control.matlab import *
from matplotlib import pyplot as plt
import pandas as pd
import sys
from scipy.optimize.minpack import transpose
df = pd.read_csv('test_data_1st.csv') # 入出力応答の読み込み
u=df['u'].values #入力データ列読み込み
t=df['t'].values #時間データ列読み込み
y=df['y'].values #出力データ列読み込み
ref=df['ref'].values #出力データ列読み込み
# 以下PID制御器更新
Ts=0.5 #規範モデルの時定数
Td=tf([1],[Ts,1])
L=Td #プレフィルタ(カスタマイズしたい場合はここを任意のプレフィルタに差し替えてください)
intg=tf([1],[1,0]) # 積分
dif=tf([1,0],[0.1,1])# 微分
(y1p, T1p, x1p )=lsim(L*(1-Td)/Td,y,t)# P制御擬似誤差
(y1i, T1i, x1i )=lsim(L*intg*(1-Td)/Td,y,t) # I制御擬似誤差
(y1d, T1d, x1d )=lsim(L*dif*(1-Td)/Td,y,t) # D制御擬似誤差
(y2a, T2a, x2a )=lsim(L,u,t) #
valb=input("PI制御なら1、PID制御なら2を入力してください:")
if valb != '1' and valb !='2':
sys.exit('エラーが発生しました。もう一度プログラムを実行してください')
else:
if valb=='1':
A=[y1p,y1i] # PI制御の場合
if valb=='2':
A=[y1p,y1i,y1d] # PID制御の場合
invA=np.linalg.pinv(A) #擬似逆行列
rho=y2a@invA #最適パラメータの求解
if valb=='1':
print('PIゲイン更新結果:','kp=',rho[0],':ki=',rho[1]) #PIパラメータ確認
if valb=='2':
print('PIDゲイン更新結果:','kp=',rho[0],':ki=',rho[1],':kd=',rho[2]) #PIDパラメータ確認