NMF(非負値行列因子分解）の初期値問題

この記事は古川研究室 Advent_calendar 11日目の記事です。
本記事は古川研究室の学生が学習の一環として書いたものです。内容が曖昧であったり表現が多少異なったりする場合があります。
#はじめに
前回の記事はNMFとは何なのか？などNMFを初めて勉強する方への記事でした。本記事ではsklearnのNMFライブラリーを実装し初期値による誤差の違いを見ていきます。

#NMFの初期値問題
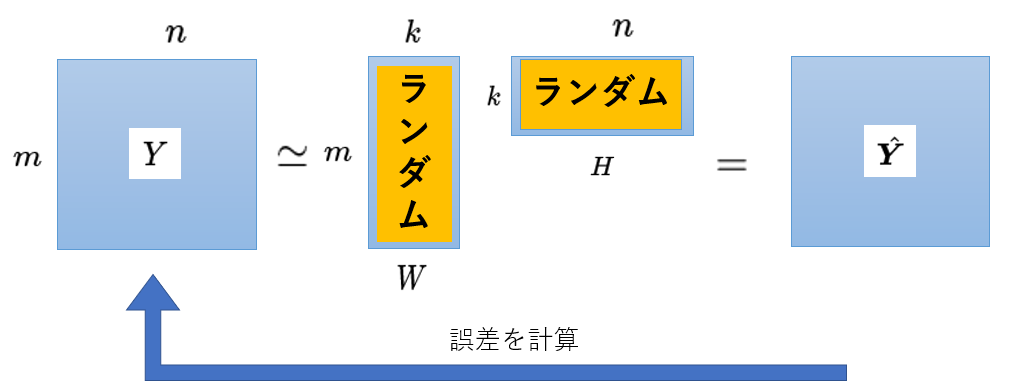
NMFでは学習を始める前に$W,H$の初期値を設定する必要があります。下の図は学習１回目の初期値をランダムにした場合です。$W,H$にランダムな値を当てはめて学習1回目の推定値$\hat{Y}$を計算します。その後元データ$Y$との誤差を計算し、$||Y-\hat{Y}||$が小さくなるように$W,H$を更新していきます。このランダム初期値の場合、学習後の推定値$\hat{Y}$がランダム値によって異なります。つまりランダム値により毎回違う推定値$\hat{Y}$が出てきてしまうという問題があります。NMFの初期値問題を解決する方法は多々あるのですが、一定の推定値$\hat{Y}$を得るためにsklearnのNMFライブラリーではランダム初期化以外にnndsvd,nndsvda,nndsvdarを選択でき、これらの手法で初期化すると一定の推定値を求めることが出来ます。nndsvdについては参考論文[1]こちらをご覧ください。

#sklearn.decomposition.NMF
sklearnのNMFでは初期化方法に5種類選択できます。
今回はカスタム初期値以外の4種類（nndsvd,nndsvda,nndsvdar,random)の手法を比較します。
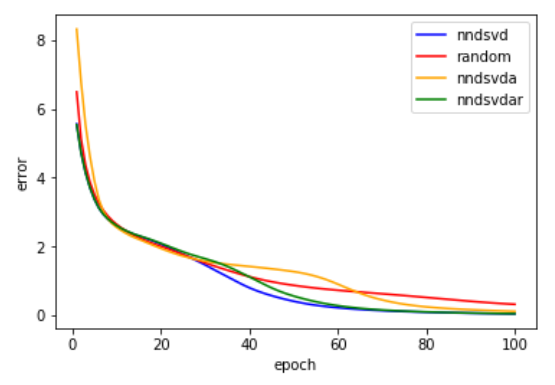
誤差はフロベニウスを用いています。比較結果が以下になります。

randomは10回の平均誤差を表示しています。100回学習するとランダム初期値よりも他の手法の誤差が小さくなっています。またnndsvd,nndsvdarは学習初期段階での誤差がランダムより小さいことが分かります。よってこのデータに関しては初期値にnndsvdを用いた方がよさそうです。

#Python code

from sklearn.decomposition import NMF
import matplotlib.pyplot as plt
import numpy as np

np.random.seed(1)
X = np.random.rand(100, 10)
x_plot=np.arange(1,11,1)
time=100
x_plot_t = np.arange(1, time+1, 1)

loss_t = np.ones(time)
loss_t1 = np.empty((time,100))
loss_t2 = np.empty(time)
loss_t3 = np.empty(time)


for j in range(time):



    model_t = NMF(n_components= 10, init='nndsvd', random_state=1, max_iter=j+1, beta_loss=2,solver='cd')# ,l1_ratio=1,alpha=0.7)
    Wt = model_t.fit_transform(X)
    Ht = model_t.components_
    loss_t[j] = model_t.reconstruction_err_


    model_t2 = NMF(n_components=10, init='nndsvda', random_state=1, max_iter=j + 1, beta_loss=2,solver='cd' )#,l1_ratio=1,alpha=0.7)
    Wt2 = model_t2.fit_transform(X)
    Ht2 = model_t2.components_
    loss_t2[j] = model_t2.reconstruction_err_

    model_t3 = NMF(n_components=10, init='nndsvdar', random_state=1, max_iter=j + 1, beta_loss=2,solver='cd')# ,l1_ratio=1,alpha=0.7)
    Wt3 = model_t3.fit_transform(X)
    Ht3 = model_t3.components_
    loss_t3[j] = model_t3.reconstruction_err_
    
for j in range(100):
    
    for r in range(10):
        model_t1 = NMF(n_components=10, init='random', random_state=r, max_iter=j+1, beta_loss=2,solver='cd')#, l1_ratio=1, alpha=0.7)
        Wt1 = model_t1.fit_transform(X)
        Ht1 = model_t1.components_
        loss_t1[j,r] = model_t1.reconstruction_err_
    
    
    
    
loss_t1 = np.sum(loss_t1, axis=1) * 0.1
plt.plot(x_plot_t,loss_t,label="nndsvd",color='b')
plt.plot(x_plot_t, loss_t1,color='red',label="random")
plt.plot(x_plot_t, loss_t2,label="nndsvda",color='orange')
plt.plot(x_plot_t, loss_t3,label="nndsvdar",color='g')


plt.xlabel("epoch")
plt.ylabel("error")
plt.legend()
plt.show()

#参考文献
[1] http://scgroup.hpclab.ceid.upatras.gr/faculty/stratis/Papers/HPCLAB020107.pdf
[2] https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.NMF.html