リッジ回帰の実装

はじめに

この記事は古川研究室 Workout_calendar 15日目の記事です。
線形回帰の勉強をしたら自ずとリッジ回帰も出てくると思います。線形回帰と何が違うんだろうと思ったので記事にしてみました！

リッジ回帰とは

リッジ回帰とは過学習を防ぐため線形回帰に正則化項(ペナルティ項)としてL2ノルムを導入したモデルです。ざっくり説明すると過学習を抑える手法の一つとも言えます。

線形回帰での過学習

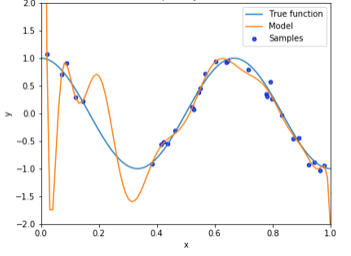
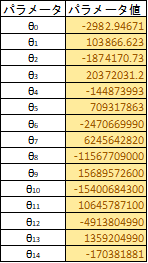
真の関数を$\cos$関数としノイズを乗せてプロットした点に多項式でフィッティングすると以下の図のように過学習してしまいます。これでは新しい入力に対して正確な予想ができません。ここで過学習を起こしているモデルのパラメーター$\theta$を確認してみます。パラメータ値が大きくなっていることがわかります。このように、過学習の特徴として学習したパラメータ値が大きくなる性質があります。そこでリッジ回帰ではこのパラメータ値が大きくならないように正則化項を用います。正則化項は様々ありますが、リッジ回帰ではL2ノルムを正則化項で用います。L1ノルムを用いるとラッソ回帰になります。

　　　　　　　

線形回帰により$cos$関数を14次多項式(下記)でフィッティングした様子（上図）
　
$y=θ_{14}x^{14}+θ_{13}x^{13}+θ_{12}x^{12}...+θ_{1}x+θ_{0}$

リッジ回帰における正則化項の働き

先ほど述べた通り、線形回帰で過学習を起こすとパラメータの絶対値が増加します。
よってここではL2ノルムによりどのようにパラメータ値の増加化を防ぐのかを具体的にみていきます。まずは線形回帰から説明します。線形回帰では主に最小二乗法で誤差を求め、勾配降下法(他の手法もあります)で誤差を最小にするパラメータを求めます。(勾配降下法の説明は省きます)

最小二乗誤差$J_{LS}(\theta)$は以下の式で示します。

$J_{LS}(\theta)=\displaystyle{\frac{1}{2}\sum_{i=1}^{N}(f_{\theta}(x_{i})-y_{i})^2}$

リッジ回帰ではこの二乗誤差に正則化項(L2ノルム)を加えます。
$J_{LS}(\theta)=\underset{\Large二乗誤差}{\underline{\displaystyle{\frac{1}{2}\sum_{i=1}^{N}(f_{\theta}(x_{i})-y_{i})^2}}}+\displaystyle\underset{\Large正則化項}{\underline{\frac{1}{2}\lambda\sum_{j=1}^{M}(\theta_{j})^2}}$

正則化項をよくみるとパラメータ $\theta_{j}$ の2乗があるのが分かります。高次多項式において二乗誤差だけを最小化しようとするとパラメータ値が増大し(過学習)、プラスされている正則化項の値が大きくなってしまいます。
　リッジ回帰ではこの正則化項を加えた状態での最小誤差を求めているので、$\theta_{j}$が大きくなるようなパラメータ値は選択しません。よって過学習を防ぐことができます。

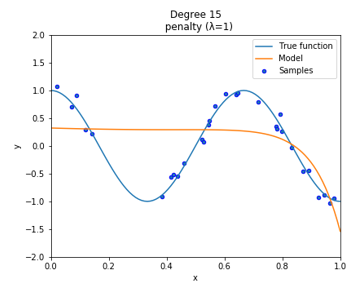
次に、正則化項には $\lambda$ を含んでいるのが分かります。これは正則化項の影響の強さを示しています。$\lambda$ はハイパーパラメータなので、事前に値を決めておく必要があります。$\lambda$を小さくすると正則化項の影響が小さくなり $\lambda=0$ にすると正則化項が消滅します(線形回帰)。逆に$\lambda$を大きくすると正則化項の影響が強くなります。以下の図は$\lambda$の値を大きくした場合のリッジ回帰を実装したものです。($\lambda=1$ 、14次多項式でフィッティング)

　　

右側のパラメータ値が0に近い値になっているのが分かります。これはこれ以上正則化項の値を大きくしないように$\theta$の値を0に近づけるように学習していると言えます。このように$\lambda$は適切な値に設定しないと不適切なモデルになることがあります。モデルによって様子を見ながら適切な $\lambda$ を選択する必要があります。なんだか罰が強すぎて何もできねぇって感じですね。

リッジ回帰でのノルムのイメージ

次にノルムについて解説します。
イメージしやすいように1次関数による二乗誤差を考えます。

y=θ_{1}x+θ_{0}

この関数をリッジ回帰式にあてはめると以下のようになります。

J_{LS}(\theta)=\displaystyle\frac{1}{2} \sum_{i=1}^{n}(y_{i}-(θ_{1}x_{i}+θ_{0}))^2 +\frac{λ}{2}((θ_{1})^2+(θ_{0})^2)　\lambda>0

ここで正則化項の中身である$(θ_{1})^2+(θ_{0})^2$に注目します。これがL2ノルムなのですが、円の方程式になっていることが分かります。
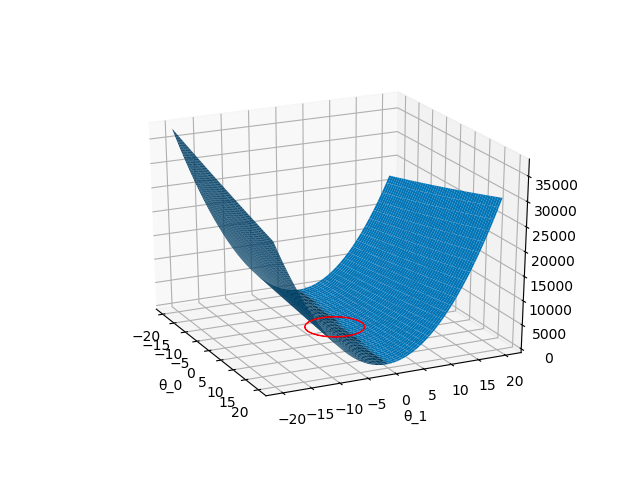
L2ノルムのイメージとしてはxyz軸にそれぞれ{$\theta_{0},\theta_{1},$二乗誤差}をとります。するとxyz空間に各パラメータ値 $\theta_{0},\theta_{1}$における二乗誤差値からなる曲面を構成します。
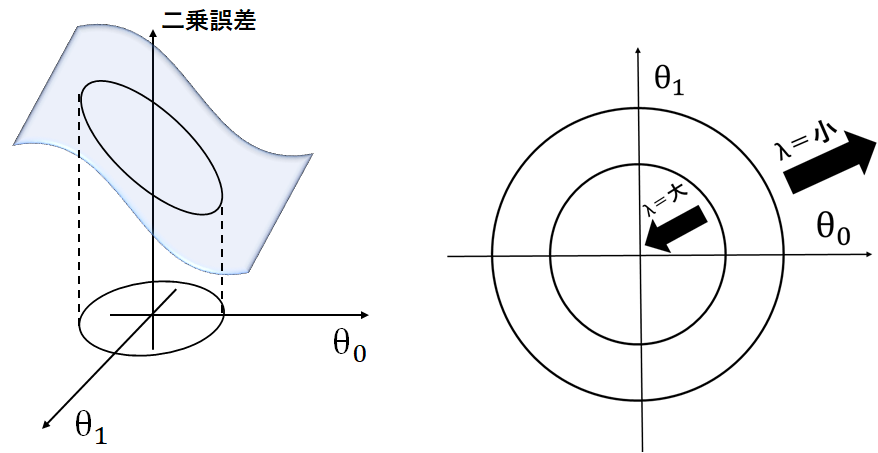
正則化項がないとこの平面の全ての範囲から二乗誤差を最小にする$\theta_{0},\theta_{1}$を選択します。正則化項を導入すると下図のように、円の範囲内から二乗誤差を最小にする$\theta_{0},\theta_{1}$を選択します。高次関数でも同様に二乗誤差を最小にするパラメータ値の範囲を制限することで過学習を防いでいるのです。
　$\theta_{0},\theta_{1}$の選択範囲である円の半径は正則化項の$\lambda$を調整することで可能です。$\lambda$ を小さくすると正則化項の値が小さくなり$\theta_{0},\theta_{1}$を選ぶ範囲が大きくなります。

実際にpythonで二乗誤差の平面を描写したものが以下になります(1次関数です)。先ほど述べた通り、L2ノルムを導入すると赤い円の範囲から二乗誤差を最小にするパラメータを選択します。実際、円の半径は$\lambda$によって変化するので下図はあくまでもイメージです。

L2ノルムは円形ですが $θ_{0},θ_{1}$の選択範囲の形状はノルムによって変化します。
ノルムによる範囲形状の変化は下図のようになります。特定のパラメータ値を0にしたい場合はL1ノルムを使うなど、必要に応じてどのノルムを使うのか検討するのが良いと思います。

$|\theta_{0}|^p+|\theta_{1}|^p$

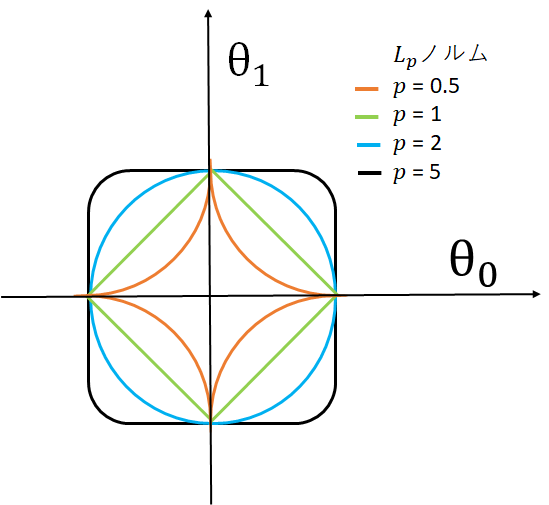
リッジ回帰の実装（Python）

実際にpythonでリッジ回帰を実装してみましょう。
真の関数は$\cos$関数で、データ点は$\cos$関数にノイズを加えたものを用意しました。
また、比較対象として $λ=0$ の場合(ペナルティ項を0にしたもの)を用意しました。
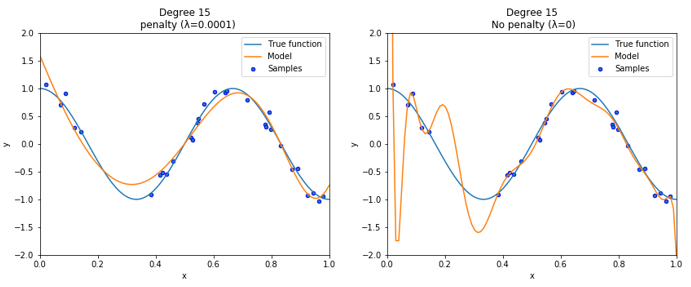
フィッティングモデルは14次の多項式です。

上図がpythonでの実行結果です。左側がリッジ回帰、右側はペナルティ項を0（線形回帰）にしたものです。リッジ回帰では過学習が抑制されているのが分かります。ハイパーパラメータである $\lambda$ はうまくフィッティングできるように $\lambda=0.0001$ としました。

以下にプログラムを載せています。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import Ridge
from sklearn import linear_model

def true_fun(X):
    return np.cos( 3*np.pi * X)

np.random.seed(0)
n_samples = 30 #30個の点を用意
degrees = [15] #14次
X = np.sort(np.random.rand(n_samples))
y = true_fun(X) + np.random.randn(n_samples) * 0.1  #真の関数にノイズを乗せる。

plt.figure(figsize=(14, 5))
for i in range(len(degrees)):
    ax = plt.subplot(1, len(degrees), i + 1)
    plt.setp(ax, xticks=(), yticks=())

    polynomial_features = PolynomialFeatures(degree=degrees[i],
                                             include_bias=False)  　　 #多項式の定義
    linear_regression = linear_model.Ridge(alpha=0.0001)               #リッジ回帰の定義

    pipeline = Pipeline([("polynomial_features", polynomial_features),
                         ("linear_regression", linear_regression)])
    pipeline.fit(X[:, np.newaxis], y)

    # 評価
    scores = cross_val_score(pipeline, X[:, np.newaxis], y,
                             scoring="neg_mean_squared_error", cv=10)
    reg=linear_regression
    reg.coef_
    print(reg.coef_)




    linear_regression2 = linear_model.Ridge(alpha=0.0)
    pipeline2 = Pipeline([("polynomial_features", polynomial_features),
                         ("linear_regression", linear_regression2)])
    pipeline2.fit(X[:, np.newaxis], y)

    # 評価
    scores2 = cross_val_score(pipeline2, X[:, np.newaxis], y,
                             scoring="neg_mean_squared_error", cv=10)


    reg=linear_regression2
    reg.coef_
    print(reg.coef_)





    #plt.figure(figsize=(3, 3))
    plt.subplot(1,2,1)


    X_test = np.linspace(0, 1, 100)  #０から１の間に100個の等差数列を作る。
    #学習した関数
    plt.plot(X_test, true_fun(X_test), label="True function")
    plt.plot(X_test, pipeline.predict(X_test[:, np.newaxis]), label="Model")
    plt.scatter(X, y, edgecolor='b', s=20, label="Samples")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.xlim((0, 1))
    plt.ylim((-2, 2))
    plt.legend(loc="best")
    plt.title("Degree {}\n  penalty (λ=0.0001)".format(
        degrees[i], -scores.mean(), scores.std()))


    plt.subplot(1,2,2)
    plt.plot(X_test, true_fun(X_test), label="True function")
    plt.plot(X_test, pipeline2.predict(X_test[:, np.newaxis]), label="Model")
    plt.scatter(X, y, edgecolor='b', s=20, label="Samples")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.xlim((0, 1))
    plt.ylim((-2, 2))
    plt.legend(loc="best")
    plt.title("Degree {}\n No penalty (λ=0)".format(
        degrees[i], -scores.mean(), scores.std()))


plt.show()

最後に

本記事を記述するにあたり、以下の参考文献を大いに活用させて頂きました。

参考文献

書籍
イラストで学ぶ機械学習

webサイト
http://aidiary.hatenablog.com/entry/20140401/1396362757