LDAの生成過程（トピックモデル）

この記事は古川研究室 Advent Calendar 7日目の記事です。
本記事は古川研究室の学生が学習の一環として書いたものです。内容が曖昧であったり表現が多少異なったりする場合があります。
#はじめに
トピックモデルを勉強すると必ずLDAという手法を見かけると思います。しかし、実際にLDAを勉強するとこれが意外と難しくて、LDAはいったい何をやっているのだろう？？？と多くの疑問が出てきて理解するのになかなか苦労します（※私は結構苦労しました汗）。そこで本記事ではLDAを初めて勉強する方の手助けになればと思い、LDAの生成過程に注目して記事を書きました。

#Latent Dirichlet Allocation : LDA
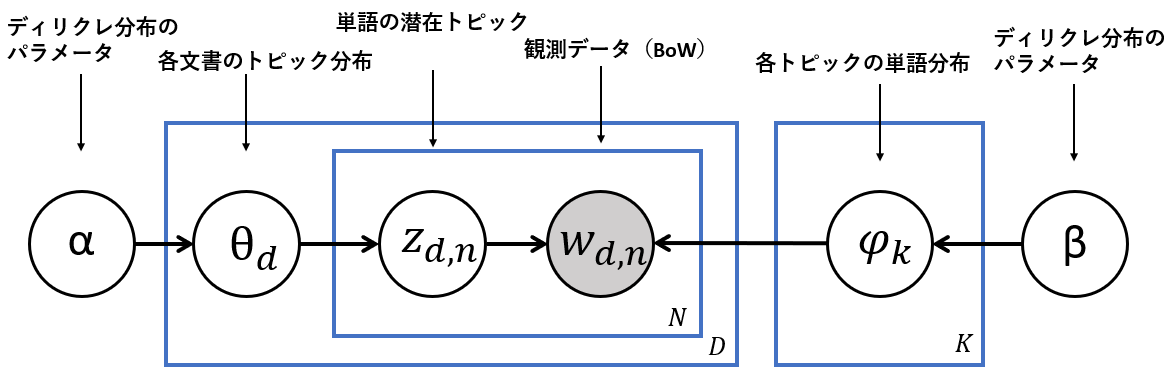
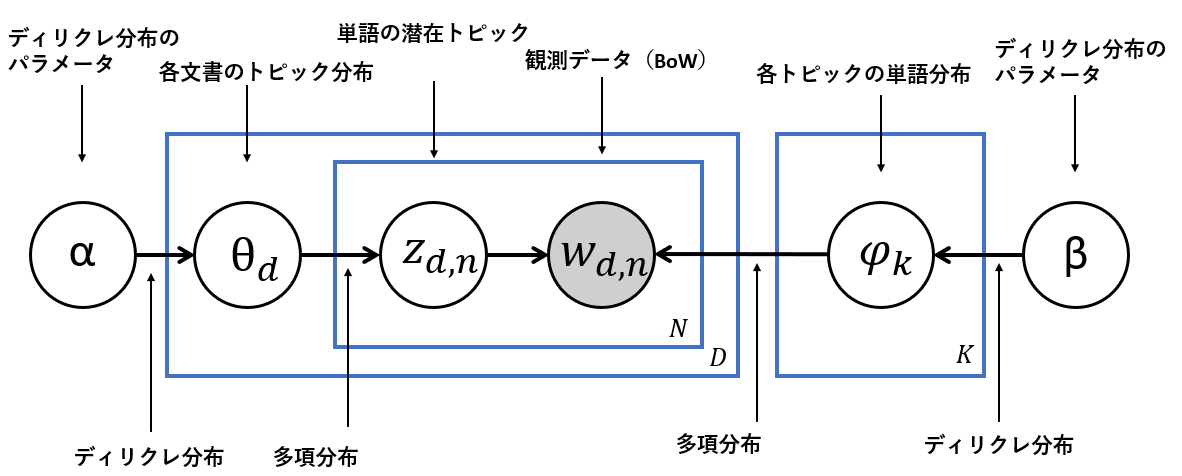
潜在ディリクレ配分法（Latent Dirichlet Allocation : LDA）はトピックモデルの代表的な手法です。下図はLDAのグラフィカルモデルで、本記事ではこのグラフィカルモデルを詳しく説明していきます。

$D:文書数$
$N:単語数$
$K:トピック数$
$\alpha,\beta:ディリクレ分布のパラメーター$
$\theta_d:各文書のトピック分布$
$z_{d,n}:単語の潜在トピック$
$w_{d,n}:$ Bag of Words
$\psi_k:各トピックの単語分布$
#LDAの生成過程

###ディリクレ分布
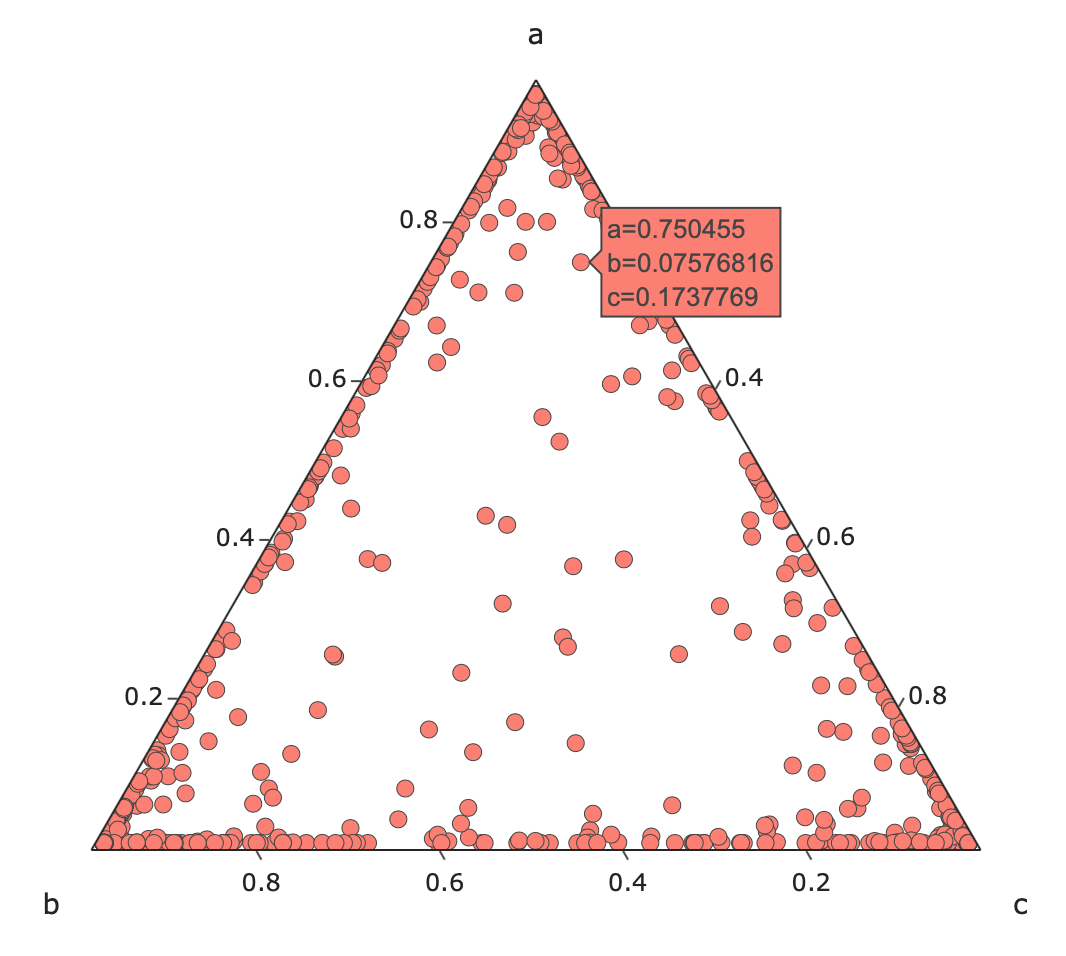
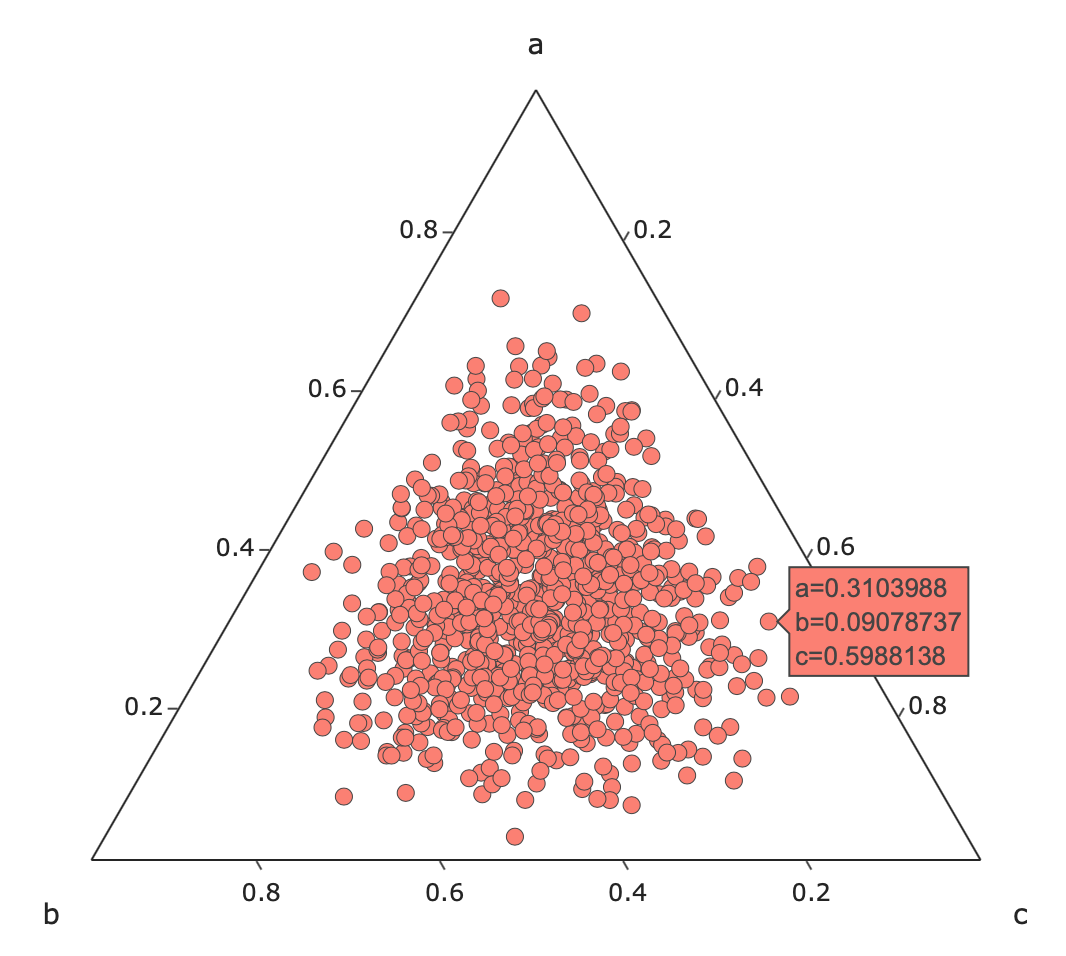
まずはLDA（潜在的ディリクレ配分法）の名前の元にもなっているディリクレ分布について説明します。下図はディリクレ分布から1000点サンプリングした結果であり、左図はハイパーパラメータである$\alpha$を$\alpha_i=(0.1,0.1,0.1)$とした場合であり、右は$\alpha_i=(5,5,5)$とした場合です。三角形の頂点であるa,b,cが事象を表しており、それらの事象がどのくらいの確率で発生するのかを表しています。例えば左の図では事象aに近い点の確率を表示しています(a=0.75,b=0.07,c=0.17)。LDAではこの a,b,c がトピックや単語に相当し、a,b,cをトピックとすると文書のトピックはこれらのトピックが均等に含んでいる(a=0.33,b=0.33,c=0.33)のではなく左図のように偏っていると見なします。また、LDAでは

LDAではディリクレ分布以外に多項分布も用います、以下に多項分布とディリクレ分布のinput,outputを図示しています。単語を例にすると多項分布では単語の総回数と単語の確率をinputとし、総回数の内それぞれの単語が何回でたかをoutputします。一方、ディリクレ分布では回数をinputとし、単語の確率をoutputします。

このディリクレ分布ですが各文書のトピック分布$\theta_d$と各トピックの単語分布$\psi_k$の生成に用います。そして多項分布は下図の位置で用います。LDAではまずこの２つのディリクレ分布のハイパーパラメータである$\alpha,\beta$を設定します。

以下ディリクレ分布のプログラムです、plotlyで実装しています。

import plotly.express as px
import numpy as np
r= np.random.dirichlet([5,5,5], size=1000)
r=r+0.02
fig = px.scatter_ternary(r,a=r[:,0],b=r[:,1],c=r[:,2],template="simple_white")
fig.update_traces(marker=dict(size=8.5,line=dict(width=0.5),color="salmon"))
fig.update_layout({
    'title': 'dirichlet',
    'ternary':
        {
        'sum':1,
        'aaxis':{'title': 'a', 'min': 0.01, 'linewidth':1, 'ticks':'outside' },
        'baxis':{'title': 'b', 'min': 0.01, 'linewidth':1, 'ticks':'outside' },
        'caxis':{'title': 'c', 'min': 0.01, 'linewidth':1, 'ticks':'outside' }
    },
})
fig.show()

###各文書のトピック分布

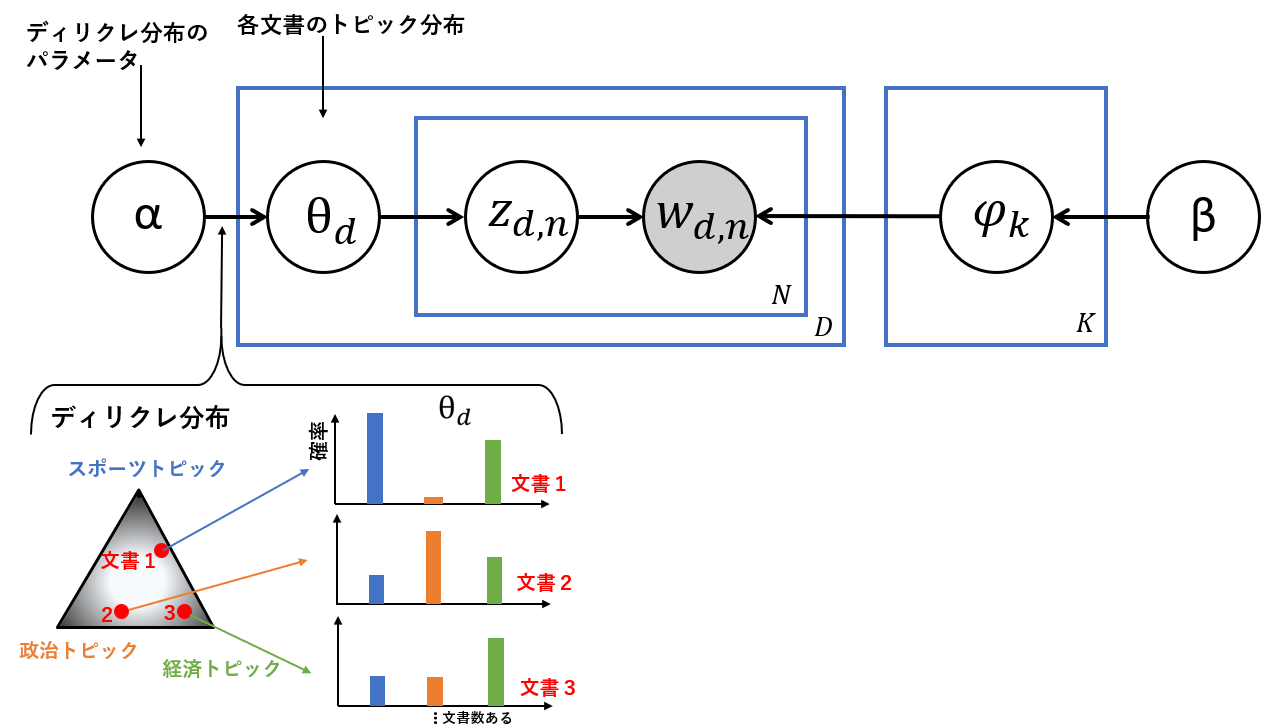
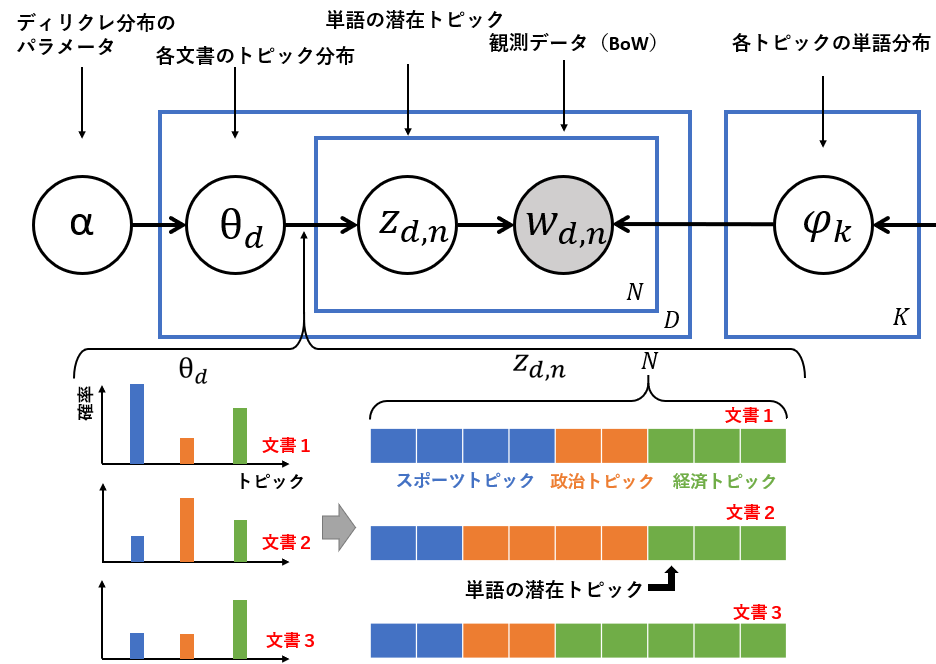
ここから生成過程を説明します。まずはグラフィカルモデルの左側から説明します。各文書のトピック分布（一つの文書のトピック割合）はディリクレ分布から得られたと仮定しています。例えば下図の文書1はディリクレ分布のスポーツトピックに近いことから、スポーツトピックの確率が一番高くなります。一方、文書3は経済トピックに近いことから経済トピック（緑色の棒グラフ）の確率が大きくなります。このように文書ごとのトピック分布を作ります。

###単語の潜在トピック
次に先ほど求めた各文書のトピック分布から単語の潜在トピックを多項分布により求めます。ここでは単語1つにトピックを1つ割り当てます。多功分布はトピックの確率と単語の総回数を入力としトピックの回数を出力します。例えば、下図の文書1ではスポーツトピックの確率が高いのでN＝9とすると4つの単語にスポーツトピックが割り振られてます。次に確率が高い経済トピックは3つの単語に割り振られ、残り2単語に政治トピックが割り当てられます。

###各トピックの単語分布
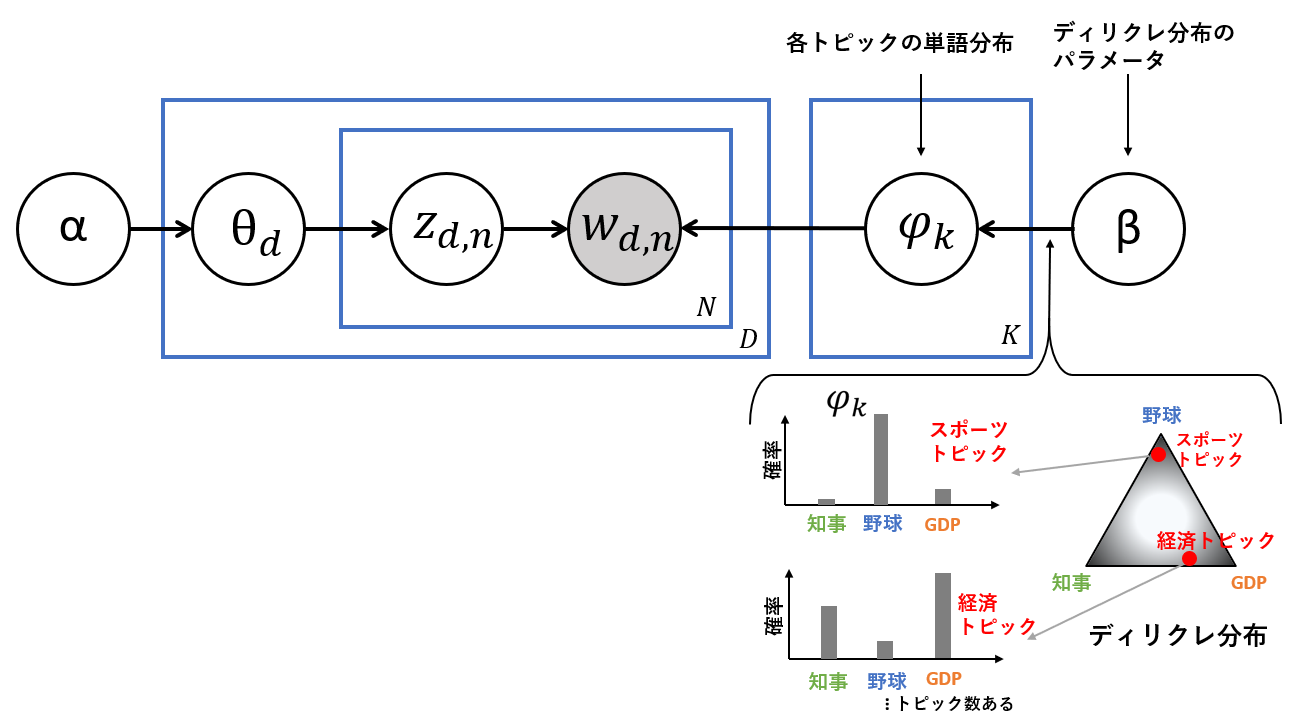
次にグラフィカルモデルの右側を説明します。各文書のトピック分布と同様に、各トピックの単語分布もディリクレ分布から生成されます。下図より（簡易にするため単語が3つの場合で考えます）例えばスポーツトピックに含まれる単語の確率はディリクレ分布より「野球」の確率が一番高いです。また、経済トピックではGDPと知事の確率が高くなっています。

###bag of wordsの生成
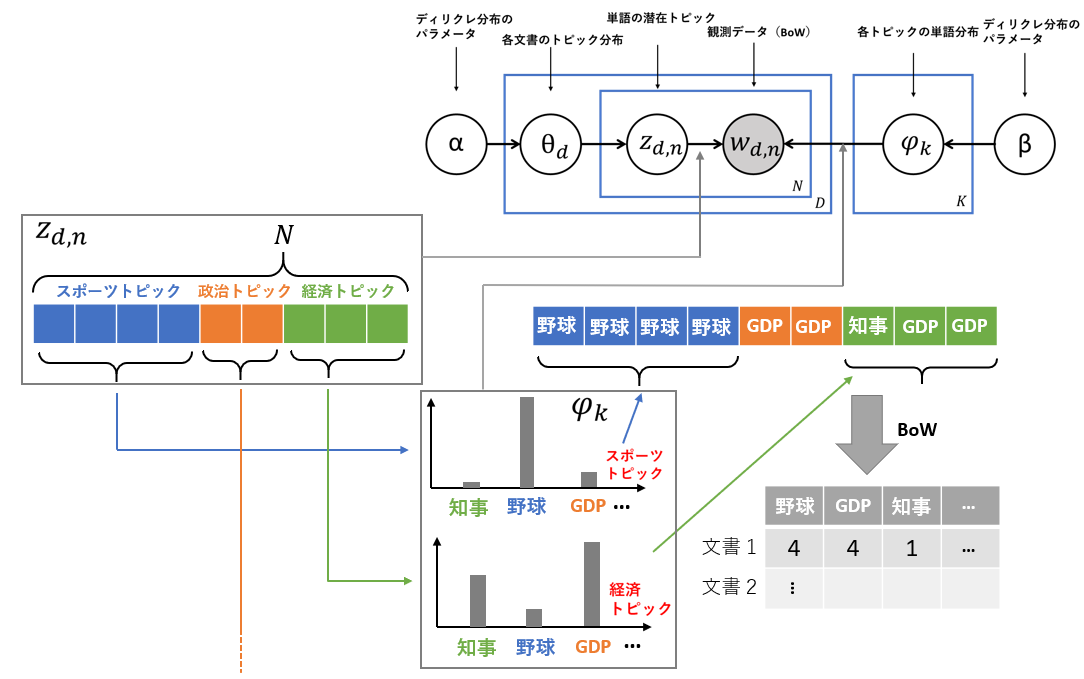
最後にグラフィカルモデル中央の$w_{dn}$です。グラフィカルモデル左側で求めた単語の潜在トピックとグラフィカルモデル右側で求めた各トピックの単語分布を用いてbag of wordsを生成します。この部分は多項分布なので、確率と総回数を入力とし、回数を出力します。下図の例だと一つの文書の単語に割り振られている潜在トピックを一つ選択し、選択したトピックの単語分布から確率の高い単語が選ばれる流れになります。（スポーツトピックは4つの単語に割り振られているので、スポーツトピックの単語分布から4回単語を選択します。野球の確率が高いので今回はたまたま4回とも野球が選ばれたと仮定しています。）LDAではこのような過程を踏むことでbag of wordsが生成されているとしています。

###LDAの数式
最後にLDAの数式を説明します。
LDAの数式は以下のようになっていて一見難しそうですが、部分ごとに見ていくと理解しやすいです。

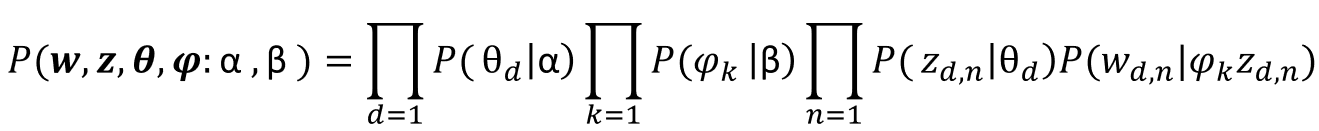
$d:文書$
$n:単語$
$k:トピック$
$\alpha,\beta:ディリクレ分布のパラメーター$
$\theta_d:各文書のトピック分布$
$z_{d,n}:単語の潜在トピック$
$w_{d,n}:$ Bag of Words
$\psi_k:各トピックの単語分布$
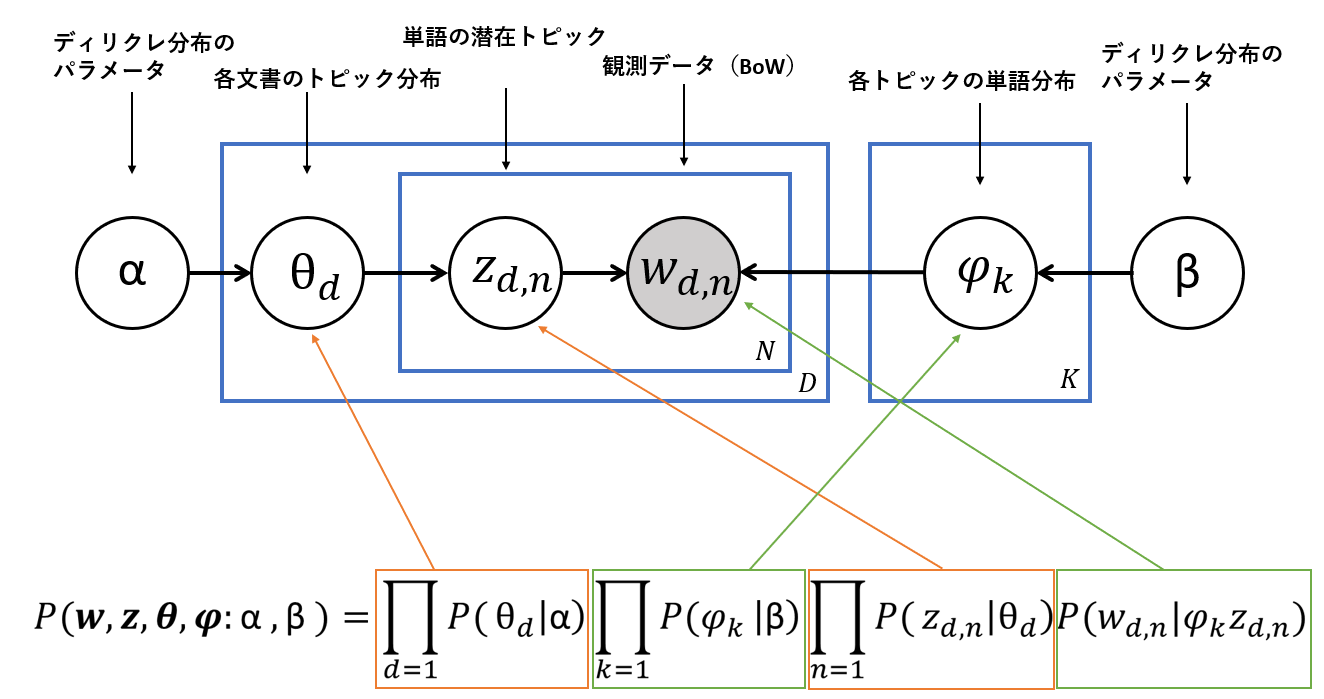
下図は数式がグラフィカルモデルのどの部分についてなのかを図示したものです。数式それぞれの部分が各文書のトピック分布（確率）、各トピックの単語分布（確率）、単語の潜在トピック（確率）、観測データ（確率）に相当しています。ちなみに各文書のトピック分布、各トピックの単語分布がLDAのoutputになります。

#参考文献
LDAの説明がとても分かりやすい動画です！
https://m.youtube.com/watch?v=T05t-SqKArY

LDAの記事
https://bookdown.org/Maxine/tidy-text-mining/latent-dirichlet-allocation.html

LDAのwikiです。
https://en.wikipedia.org/wiki/Latent_Dirichlet_allocation