概要

ベイズ推定を学習中です。
そのために確率的プログラミングライブラリEdwardを利用して、ベイズ推定を用いた機械学習を行いました。
私自身、未熟であり学習中の事柄ですので、つっこみどころありましたらコメントいただけると幸いです。

ベイズ推定

よく使われる機械学習は、データを学習後にパラメータが ひとつ に定まる。
一方、ベイズ推定を用いた機械学習は、データを学習後にパラメータが 確率的 になる。

例えば回帰分析を行った場合、式のパラメータAおよびBが確率的に表現できる。
よって予測したyも確率で表現できる。

y = AX + B

利点

パラメータを確率的に表現することができるので、初期パラメータを任意の確率分布で設定できる。
学習前にも事前の経験則をモデルに適用することができる
つまり極論、データがなくても予測ができる

個人的には下記のような利用イメージ

フランチャイズチェーンの会社があり、購買の需要予測をしている。
既存店舗はすでに長いこと運営しており、多くのデータが存在している
新しく店舗をたてることになった。新規店舗でも需要予測をしたい
新規店舗でデータが増えるまでは、既存店舗で得た分布を初期パラメータとして利用する

また、その仕組みから学習後の予測モデルから、さらに再学習が容易に可能。

Edwardについて

Edward
Pythonのライブラリで、TensorFlowを利用した確率的プログラミングができる。
確率的プログラミングとは何かは理解できていないので割愛する。上記で記載したベイズ推定による回帰分析ができると話題。

pipでインストールできる。

$pip install edward

※この記事では他にpandas、numpy、tensorflowをつかう

Edwardを用いた回帰分析

定番のirisデータセットを利用して回帰分析を行う

花の"がくの大きさ"から"花弁の大きさ"を予測する。

SepalLength(がくの大きさ)
PetalLength(花弁の大きさ)

公式サイトの下記ページを参考にする。
Edward-Supervised Learning (Regression)
Edward-Iterative estimators (“bayes filters”) in Edward?

epoch毎にデータセットからランダムにデータを10個取り出して、学習を行う。
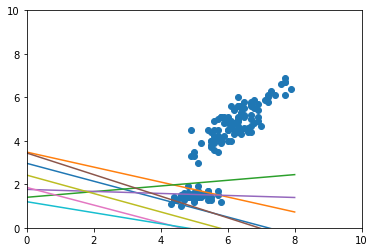
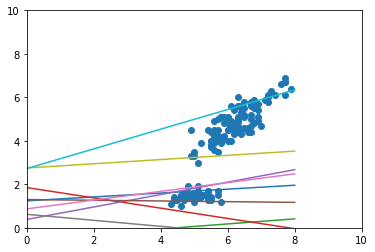
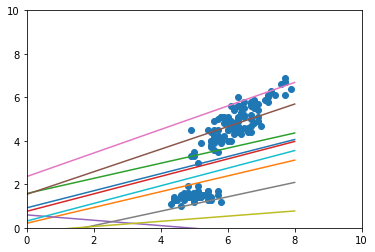
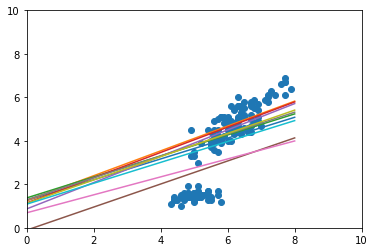
epochが進むごとに、パラメータが確率的に求まる->複数の予測モデルができあがるので、そのモデルをグラフに描画する。

初期段階
中期段階
後期段階
学習完了時

予測モデルが徐々にデータにフィットしていくことが確認できる
学習完了時にも複数の予測モデルがある
上のデータの固まりだけではなく、下のデータの固まりにひっぱられる予測モデルがある（こういうところが多分うれしい）

上記の実験のコードを下記に記載する。

edward_iris.ipynb

import tensorflow as tf
import edward as ed
import numpy as np
import pandas as pd
from edward.models import Normal
import matplotlib.pyplot  as plt

def visualise(X_data, y_data, w, b, n_samples=10):
    w_samples = w.sample(n_samples)[:, 0].eval()
    b_samples = b.sample(n_samples).eval()
    plt.xlim(0, 10)
    plt.ylim(0, 10)
    plt.scatter(X_data[:, 0], y_data)
    inputs = np.linspace(-8, 8, num=400)
    for ns in range(n_samples):
        output = inputs * w_samples[ns] + b_samples[ns]
        plt.plot(inputs, output)
    plt.show()

# irisデータを利用する
df_iris = pd.read_csv("iris.csv")
# 説明変数
feature = ["SepalLength"]
# 目的変数
target = "PetalLength"

# バッチの数
N = 10
# 説明変数の次元数
D =  len(feature)

# バッチデータを生成する
def next_batch(df, M):
    # バッチサイズでサンプリングする
    sample = df.sample(n=M)
    x = sample[feature].values
    y = sample[target].values
    return x, y

# モデルを作成する
# Xの箱を作成
X = tf.placeholder(tf.float32, [None, D])
# loc: mu 平均, scale: sigma　分散
# mu=0, sigma:1
# 係数 weight
w = Normal(loc=tf.zeros(D), scale=tf.ones(D))
# 切片 bias
b = Normal(loc=tf.zeros(1), scale=tf.ones(1))
#  一次関数を作成する
y = Normal(loc=ed.dot(X, w) + b, scale=1.0)


#　初期データ
X_batch, y_batch = next_batch(df_iris, N)

# 事前分布/事後分布
# **パラメータが確率的=>予測するための式がいっぱいあると考える**
# 学習することで、複数の式が一つの式に収束していく
# mu = 正規分布, sigma = 0以上(正規分布からsoftplus関数を利用して0以上に変換)
# 係数 weight
qw = Normal(
    loc=tf.Variable(tf.random_normal([D])),
    scale=tf.nn.softplus(tf.Variable(tf.random_normal([D])))
)
# 切片 bias
qb = Normal(
    loc=tf.Variable(tf.random_normal([1])),
    scale=tf.nn.softplus(tf.Variable(tf.random_normal([1])))
)

# 推測を初期化
inference = ed.KLqp({w: qw, b: qb}, data={X: X_batch, y: y_batch})
inference.initialize()
tf.global_variables_initializer().run()

for _ in range(inference.n_iter):
    if(_ % (int)((_ / 10) + 1) == 0):
        # グラフに描く
        visualise(df_iris[feature].values, df_iris[target].values, qw, qb)
    # 新しいデータを取り出す
    X_batch, y_batch = next_batch(df_iris, N)
    info_dict = inference.update({X: X_batch, y: y_batch})
    inference.print_progress(info_dict)

以上。

Edwardを使ってベイズ推定のイメージをつかむ実験

概要

ベイズ推定

利点

Edwardについて

Edwardを用いた回帰分析