はじめに
ちょっと前に出た機械学習のゼミでCourseraの教材を扱っていたので復習がてらアウトプットしていこうと思います。Week5の課題であるex4は、もともとはOctaveで書かれているので自己流Pythonで記述します。当然処理にかかる時間は長〜くなるので実用目的ではなく勉強目的の人に向けて書いてますのであしからず。PyTorchやTensorFlowなどの機械学習ライブラリは使いません。
今回はまずどんな目的、方向でコードを書くのかという話をしていきます。
(全然関係ないですが名詞の「話」を「話し」って書かれると凄い気になります)
ソースコードを見たい方はこちら
Mkamono/Letter_identify/letter_identify.py
とりあえず動かしたい方はこちら
Mkamono/Letter_identify
(よくわかんない方は「code」→「Download zip」でファイルごとダウンロードしてください)
世界一わかりやすいCourseraのスライドはこちら
Coursera-Machine-Learning-Stanford/ex4.pdf
※注意
今回は概要編となります。__コードはほぼ書かない__のでニューラルネットワークの構造は理解しているという方はこちらの実践編にどうぞ
Pythonで文字認識ニューラルネットワーク構築【Coursera Machine Learning】(2.実践)
環境
今回はコーディングは無しなので環境について述べる必要は特にないですが一応
- windows 10 home
- VScode 1.6.0
- Python 3.8.11
概要
全体の流れを理解することは学習の効率を高めてくれます。理解は全体から部分へ、実装は部分から全体へと進めることが理想です。
全体像
データセットとして20×20ピクセルの画像を使用します。それぞれの画像はグレースケールで1〜10までの数字が書かれています。このデータセットを学習させていきます。
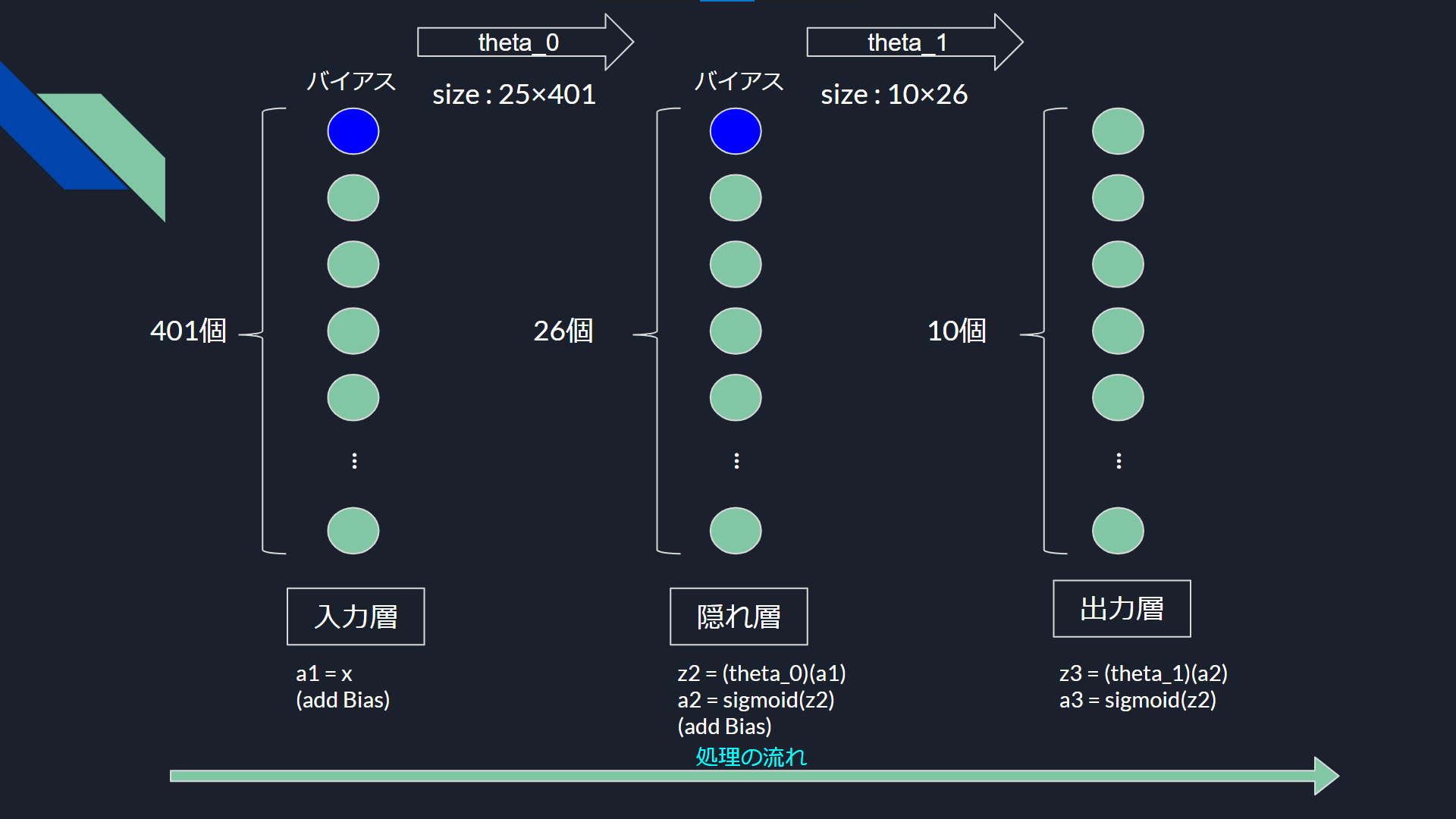
今回構築するニューラルネットワークの全体は画像のとおりです。

入力層は画像一枚のサイズ400とバイアスユニットがあり401個のノードを持っています
隠れ層は25+1、出力層は分類カテゴリの個数の10個のノードを持ちます。
大きな流れとして フォワードプロパゲーション と バックプロパゲーション の2つがあります。
前者は未知のデータに対しての予測をし、後者は既知のデータを学習する流れです。
フォワードプロパゲーション
- 入力の_x_をそのまま_a1_にセットする
- _a1_にバイアスを追加
- _a1_に_theta0_を左から作用させ25サイズの_z2_を得る
- _z2_にシグモイド関数を使い_a2_を得る
- _a2_にバイアスを追加
- _a2_に_theta1_を左から作用させ10サイズの_z3_を得る
- _z3_にシグモイド関数を作用させて_a3_を得る
理解するのは簡単かなと思います。先程のスライドがとても簡潔にまとまっていると思います。
バックプロパゲーション
データを学習していくプロセスです
これが大問題です。処理が面倒な部分が多いので何度か読みかえしてください。
Courseraとの兼ね合いがあるので、変数名についてすこしだけ説明をします。
| Coursera | 今回のコード |
|---|---|
| δ(ギリシャ小文字) | delta |
| Δ(ギリシャ大文字) | DELTA |
| D | D |
順を追って説明します
まず_delta_は「誤差」です。フォワードプロパゲーションと逆の順番で処理をします。
- 出力の_a3_と正解の_y_の差を_delta3_にセットする
- _theta1_の転置と_delta3_を掛け、26サイズのベクトルを得る
- そのベクトルに a2, 1-a2 を要素ごとに掛けて26サイズの_delta2_を得る
- バイアスユニットの誤差に相当する_delta2[0]_を取り除く
_delta3_及び_delta2_を使います
Courseraによる_DELTA_の定義は
\Delta^{(l)} = \Delta^{(l)} + \delta^{(l+1)}(a^{(l)})^T
としてすべてのデータセットで足していくとなっていますが、これは結局
\Delta^{(l)} = \sum_{n=1}^m\delta^{(l+1)}_n(a^{(l)}_n)^T
と意味は同じです(_m_はデータセットの個数)
そしてこの_DELTA_を使って
\begin{array}{ll}\frac{\partial}{\partial \Theta_{i j}^{(l)}} J(\Theta)=D_{i j}^{(l)}=\frac{1}{m} \Delta_{i j}^{(l)} \quad \text { for } j=0 \\ \frac{\partial}{\partial \Theta_{i j}^{(l)}} J(\Theta)=D_{i j}^{(l)}=\frac{1}{m} \Delta_{i j}^{(l)}+\frac{\lambda}{m} \Theta_{i j}^{(l)} & \text { for } j \geq 1\end{array}
の計算によって微分を求めます($J(\theta)$はコスト関数)
j=0において$\Theta$の項を足さないのは、バイアスユニットに関わる_theta_を正則化させないためです。
最後に_theta_の配列から_D_の配列を引けば更新は完了です
この作業を繰り返して行けば学習が進みます。
終わりに
今回は概要編でした。自分はCourseraで結構苦戦したので、初めての人もじっくりやっていきましょう。内容が理解できた人はこちらの実践編でコードを書いていきましょう。
Pythonで文字認識ニューラルネットワーク構築【Coursera Machine Learning】(2.実践)
参考
たくさんの先駆者がいます。かなり書き方が違うところがあるのでわかりやすい方を参考にしていただければとおもいます。
この記事を書いたあとに読んでわかりやすいと思った記事
@koshian2 さんの記事Coursera Machine LearningをPythonで実装 - [Week4]ニューラルネットワーク(1)
アンドリュー先生の愛が身にしみます
Coursera Machine Learning / Andrew Ng