作りかた
前回までに最小完全ハッシュ関数がいかに便利なものかを示したので、今回はその生成方法について説明する。以下で示すロジックは、こちらの論文を元にしている。この論文では「マッピングステップ」「割り当てステップ」という段階を経てまず最初に完全ハッシュ関数を作成し、それを最後の「ランキングステップ」によって最小完全ハッシュ関数に変形する、という段階を踏む。
マッピングステップ
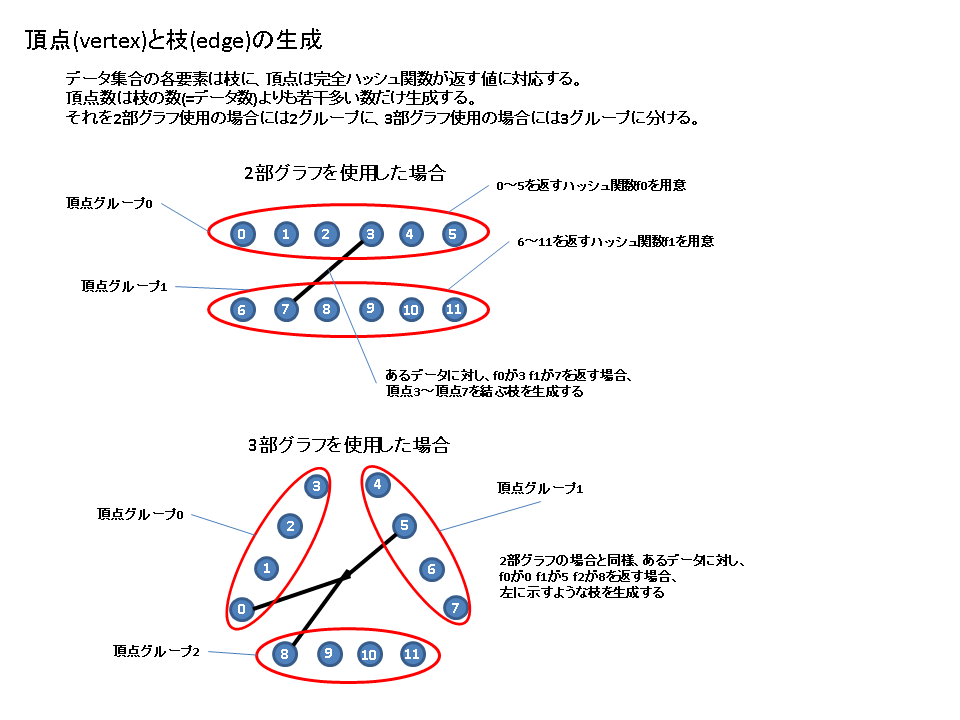
論文中では2部グラフと 3部グラフを使うやりかたが試されている。概念的にはn部グラフ(n>=2)のどれでも同じように構築可能だが、2部グラフ、3部グラフの両方の場合を図にしておく。まずは、データの数より少し多い数だけ頂点(vertex)を作成する。2部グラフの場合にはそれを二つのグループに、3部グラフの場合にはそれを三つのグループにわける。そしてそれぞれのグループから頂点を一つづつ選んだ枝(edge)をデータ数の数だけ生成する。この時、頂点の選び方としてハッシュ関数を頂点のグループの数だけ用意し、一つのデータに対して各ハッシュ関数を適用し得られたハッシュ値に応じた頂点を選ぶようにする。なお、後の説明まで読めばわかるが、枝はデータに、頂点は完全ハッシュ関数が返すハッシュ値に対応している。
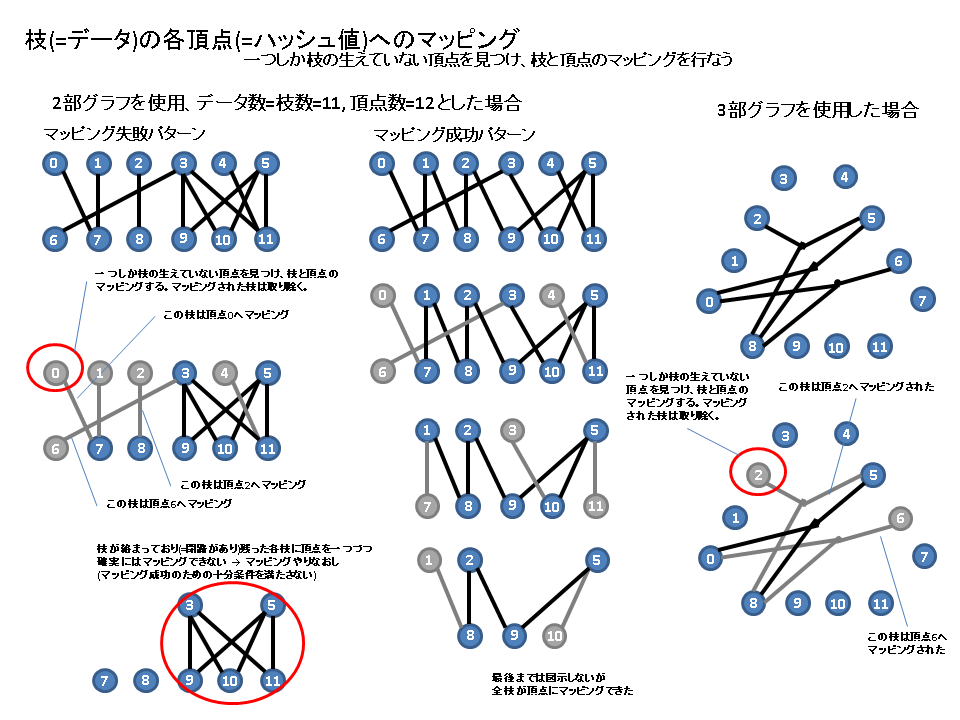
全データに対応する枝を生成し終えたら、次に一つの枝しか生えていない頂点を見つけ、そこから生えている枝のマッピング相手として頂点を対応させる。対応させられた枝は削除し、枝が全部なくなるまで枝と頂点の対応関係が生成できればマッピングステップの完了となる。もし、マッピングステップが完了せず頂点と対応できない枝が残ってしまった場合には(=グラフに閉路が存在する)別のハッシュ関数を用いて再度マッピングステップをやりなおす。
割り当てステップ
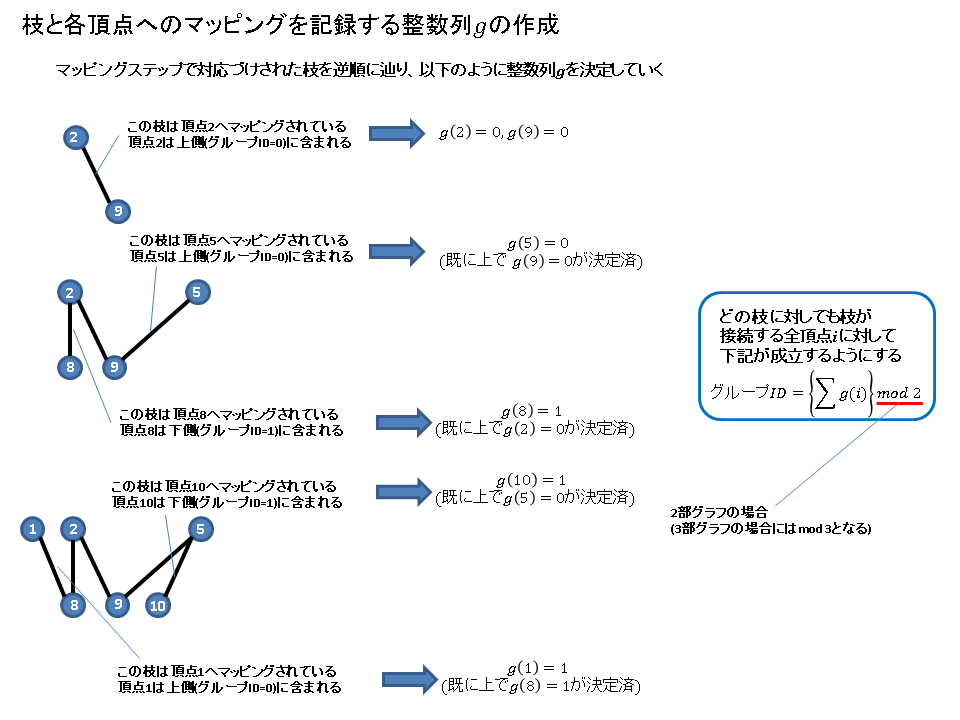
各枝が頂点へマッピングできた後、枝と頂点の対応関係を記録する整数列gを作成する。これを割り当てステップと呼ぶ。なお、gのサイズは頂点の数と同じである。まず、マッピングステップにて対応づけられた順の逆順に枝を並べる。そして以下で図示するように順に整数列gを決めていく。
なお、マッピングによっては頂点に対応するgが決定できない箇所もあるが、そのような値はどのみちハッシュ値計算に使用されないので何か適当な値を埋めておいても問題ない。後で説明するランキングステップのためには負の値やグループIDの最大値+1のような値を埋めておくのが便利である。いずれにしても、以上の手続きを経てgが決定されれば、完全ハッシュ関数の構築が完了である。ハッシュ値の求めかたは以下のようになる。
- データに対応する枝を求める(2部グラフの場合、ハッシュ関数f0, f1にて求められる値の頂点を結ぶ枝を作る。3部グラフの場合、ハッシュ関数f0, f1, f2 にて求められる値の頂点を結ぶ枝を作る)
- 枝に接続している頂点のうち、どのグループを採用するかを以下の式で求める
- 枝に接続している頂点のうち、前段で求めたグループに属している頂点のIDをハッシュ値とする
ランキングステップ
以上で構築された完全ハッシュ関数は、論文によればデータ数×1.23倍の頂点を用意すれば充分に構築可能(3部グラフを利用時)とのことで、既にかなり最小完全ハッシュ関数に近い。最後の仕上げとして、これを最小完全ハッシュ関数にするために完備辞書と呼ばれるビット列を用いる。完備辞書は以下の二つの操作が定数時間でできるビット列のことだ。
- 0~n-1番目のビットまでに true もしくは false がいくつあるか数える操作。以降 int rank(lboolean[] v, int nth, boolean b); というような関数として表現する。
- 先頭から数えてn個目の true もしくは false であるビットがk番目にあるとして、k+1を求める操作。以降 int select(boolean[] v, int n, boolean b); というような関数として表現する。
rank と select は逆関数になっていることに注目だ。つまり rank(v, select(v, n, true), true) = n となる。ここではとりあえず「定数時間で」というところを無視しておくことにする。丁度、以下のような簡素なコードがあると考えておいて先へ進むことにしよう。これでは性能が悪くて使いものにならないが…(正しく定数時間で上記操作が実行できるコードはまた後の回で示すことにする)
public static int rank(boolean[] v, int num, boolean bit) {
int result = 0;
for (int i = 0; i < num; i ++) if (v[i] == bit) result ++;
return result;
}
public static int select(boolean[] v, int nth, boolean bit) {
for (int i = 0; i < v.length; i ++) if (rank(v, bit, i) == nth) return i;
throw new IndexOutOfBoundsException();
}
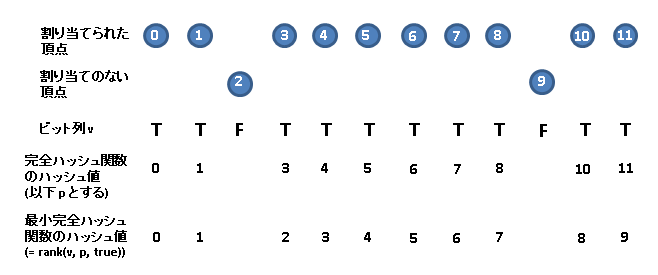
割り当てステップにて説明したように頂点の中にはハッシュ値計算に使用されないものが出てきてしまう。そのような頂点に対応するハッシュにはデータが対応せず、その分、空きが生じる。そこで完備辞書であるビット列vを用意し、頂点iが使用されていれば v(i) を true に、そうでなければ v(i)を false にする。そうすることで、上で求まった完全ハッシュ関数によるハッシュ値をpとするとrank(v, p, true)を返すようにすれば最小完全ハッシュ関数のできあがりだ。以下の図を参照すれば内容は理解できるだろう。なお、整数列gの使用されない部分もvを利用すればつめてしまうことができる。空きスロットを詰めてしまったものをg' と呼ぶことにするとg(n) = g'(rank(v, n, true))となるからで、そのようにすることでメモリを省くことができる。
ここまでのロジックを簡素なコードに落とせば Java で書いて100行にも満たないレベルで記述できる。ここまで詳細を説明すれば、もうほとんどの人が自力で最小完全ハッシュ関数を生成するロジックは書けると思う。次回、私の方でも具体的なコードを提示して動作を検証してみることにする。