はじめに
仕事の隙間に少しだけ時間ができたので数年来勉強したいと思っていた Succinct Data Structure(簡潔データ構造) について勉強してみる。勉強といっても単に論文を読むのでなく実装する方向であり、コードの方向性としては性能を目指すのでなく内容を理解しやすいできる限り簡素なコードを目指すことにする。
簡潔データ構造(Succinct Data Structure) とは何か
簡潔データ構造とは、情報理論上、下限に近いくらいまで元のデータを圧縮しながらなおかつ、効率的に検索等ができるデータ構造を指す。普通、ファイルを zip 等で圧縮してしまうと、再度使うためには一度解凍してから、というのが常識であると思う。ところが簡潔データ構造を用いると圧縮した状態そのままで、そのデータを使用することができるというのだ。初めて聞いたときにはあまりにも信じられない思いで、すぐさま論文をダウンロードし…そして自分の数学的才能のなさに絶望した。(要はすぐには理解できなかったのだ…)
今のところこのようなデータ構造はビッグデータ処理といったハイエンドな分野で使用されることが多いように見られる。しかし今後は組込み系など省メモリ性能が厳しく問われる領域でも広く使われていくことになるのだと思う。あるいは私が知らないだけでもう既に広く使われはじめているのかもしれない。いずれにしても自分の技術力を磨き続けるため、隙間時間を見つけて以前理解できなかった論文群をもう一度読みなおした結果、ある程度動く実装が作れる程度までに理解できたと思うのでここにメモを記して行こうと思う。
まずは簡潔データ構造と呼ばれるものの中でも実用上、一番応用分野が広いと(私のような素人が)考える最小完全ハッシュ関数というものをネタにしよう。
最小完全ハッシュ関数
ハッシュ関数とは「あるデータを代表する(要約する)数値を得る関数」である。Javaで言えばデータは一般にオブジェクトとして表現され、そのオブジェクトは Object.hashCode をオーバーライドした整数を返すメソッドを持っているはずである。それがまさにハッシュ関数だ。ハッシュ関数は同じデータに対しては同じ数値を返さなければならず(決定性を持つと表現される)、また与えられた値域の中に一様に分散するのが望ましい(一様性を持つと表現される)。
さて、今ハッシュ関数は同じデータに対しては同じ値を返さねばならないと書いたが、違うデータに対して違う値を必ずしも返す必要はない。JavaのObject.hashCode にはそのような説明がつけられており良く知られた話なので特に説明はいらないだろう。しかしここで仮に、あるデータ集合の各要素に対して全て異なる値を返すことのできるハッシュ関数があったとしよう。そのようなハッシュ関数は完全ハッシュ関数と呼ばれる。完全ハッシュ関数が存在する場合、それを用いて非常に簡単にハッシュテーブルが書けることになる。以下の疑似コードを見てみよう。
public class SimpleHashTable<K, V> {
private static int perfectHashFunction(K key) { // 完全ハッシュ関数 ... 以下略
private Object[] table = new Object[initialSize];
public void put(K key, V value) {table[perfectHashFunction(key)] = (Object) value;}
public V get(K key) {return (V) table[perfectHashFunction(key)];}
}
要するに完全ハッシュ関数は衝突(違うデータに対して同じ値を返してしまうこと)の心配が一切不要なので、ハッシュテーブルの実装がほぼ単なる配列の読み書きになってしまうのだ。なお、あたりまえだが配列のサイズ(上のコードで言えば initialSize)はデータ集合の要素数以上のものを確保しておく必要がある。そしていくつかのセルは対応する要素の存在しない、空いた部分となる可能性がある。
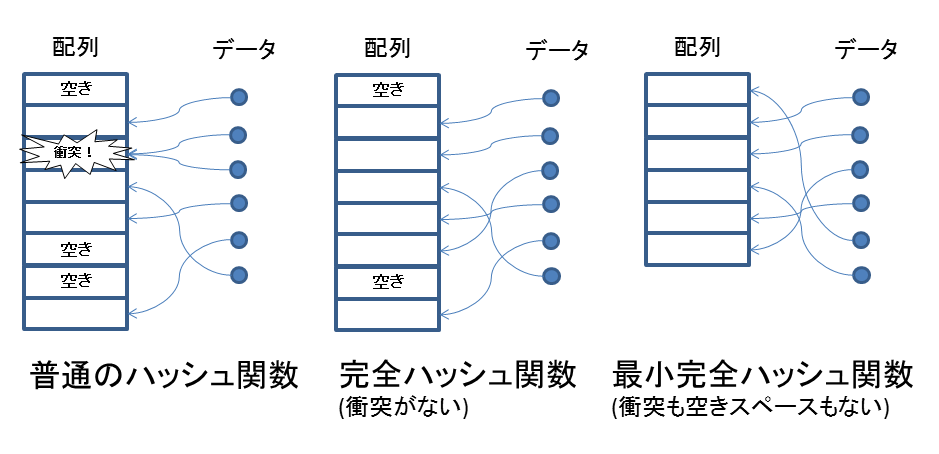
ここでもし、要素数nのデータ集合に対して0~n-1の値を返す完全ハッシュ関数が存在する場合、そのような空いた部分が存在しない、非常にメモリ効率の良いハッシュテーブルが実現する。そのようなハッシュ関数を最小完全ハッシュ関数と呼ぶ。それぞれのハッシュ関数を図にすると以下のようになる。
さて任意のデータ集合に対して、最小完全ハッシュ関数があればハッシュテーブルが非常に簡素に、かつ高いメモリ効率で実装できることはわかった。問題はそんな都合の良い関数がほいほい作れるのか、ということだ。実はできる。しかもJavaで書いて100行にもならない簡素なアルゴリズムで、だ。
以下、こちらの論文を元に解説する。………と言いたいところだが一つの記事が長くなりすぎるので、ここからは次回に回すことにしてまずは後で使うための単純なハッシュ関数を準備しておこう。素数をかけ算しながら加算していくシンプルなハッシュ関数だ。素人なのでこんな単純なハッシュ関数で実用に耐えるのか(一様性など充分なのか)良くわからなかったが、実際に試してみた結果、後で最小完全ハッシュ関数を得るための下準備としては充分な性能があった(のでたぶん問題ない)。
public static interface HashFunction {
public int hash(byte[] src);
// fromInclusive ~ toExclusive - 1 までの範囲のハッシュ値を返す。(後で最小完全ハッシュ関数を生成するのに必要となる)
public default int folded(byte[] src, int fromInclusive, int toExclusive) {return Math.floorMod(hash(src), toExclusive - fromInclusive) + fromInclusive;}
}
public static class SimpleHashFunction implements HashFunction {
protected final int prime;
public SimpleHashFunction(int prime_) {prime = prime_;}
@Override public int hash(byte[] src) {
int sum = prime;
for (byte b : src) sum = sum * prime + b;
return sum;
}
}
private static final List<Integer> primeList = Arrays.asList(
11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,
211,223,227,229,233,239,241,251,257,263,269,271,277,281,283,293,307,311,313,317,331,337,347,349,353,359,367,373,379,383,389,397,401,409,419,421,431,
433,439,443,449,457,461,463,467,479,487,491,499,503,509,521,523,541,547,557,563,569,571,577,587,593,599,601,607,613,617,619,631,641,643,647,653,659,
661,673,677,683,691,701,709,719,727,733,739,743,751,757,761,769,773,787,797,809,811,821,823,827,829,839,853,857,859,863,877,881,883,887,907,911,919,
929,937,941,947,953,967,971,977,983,991,997);