ベイズ推論において重要な役割を果たす事後分布ですが、その計算には避けて通れない壁が存在します。それが、分母の計算ができない問題です。
想定読者
- 入門と言いつつ、ベイズ推論とMCMCについて1冊くらいの本を読んでわからないようなわかったような... となっている人向けの記事になってます。
- 「事後分布の計算が難しい、というのはわかったけど、MCMCはそれをなぜ克服できるのか?どう解決しているのか?MCMCのアルゴリズムってどういう発想なのか?」という疑問に回答できるかと思います。
事後分布とは?
事後分布は、ベイズの定理によって定義される、パラメータ $\theta$ の確率分布です。データ $D$ が与えられた下で、パラメータ $\theta$ がどのような値を取りやすいのかを表します。
$$
p(\theta | D)=
\frac{p(D|\theta)p(\theta)}{p(D)}
$$
ここで、
- $p(\theta | D)$:事後分布
- $p(D|\theta)$:尤度関数
- $p(\theta)$:事前分布
- $p(D)$:周辺尤度(またはエビデンス)
なぜ分母 p(D) が計算できないのか?
この事後分布の定義式において、分母 $p(D)$ は周辺尤度と呼ばれ、以下の積分で計算されます。
$$
p(D) = \int p(\theta, D) d\theta = \int p(D| \theta)p(\theta) d\theta
$$
この分母 $p(D)$ が、ベイズ推論の実践において大きな障壁となることが多いのです。なぜなら、以下の2つの理由により、解析的に計算することが困難、あるいは計算量が膨大になるケースがあるためです。
理由①:解析的に計算できないケース
例えば、ロジスティック回帰モデルを考えてみましょう。ロジスティック回帰の尤度関数にはシグモイド関数が含まれており、この関数を解析的に積分することは一般的に不可能です。
理由②:計算量が膨大になるケース
パラメータ $\theta$ やデータ $D$ が高次元である場合、積分の次元数が増加し、計算量が指数関数的に増大します。現代のデータ分析においては、パラメータやデータが数十~数万の次元を持つことは珍しくありません。このような場合、たとえ計算機を用いたとしても、積分計算は現実的な時間内には終わりません。
MCMC(マルコフ連鎖モンテカルロ法)とは?
このような背景から、「事後分布の分母 $p(D)$ を直接計算せずに、事後分布 $p(\theta | D)$ からサンプルを生成する方法はないか?」という発想が生まれます。そして、この問題を解決するために考案された手法が、**MCMC(マルコフ連鎖モンテカルロ法)**なのです。
MCMC は、以下の2つの問題を区別して考えることで、分母の計算を回避します。
- 事後分布の形状を正確に知ること
- 事後分布からサンプルを得ること
MCMC が目指すのは、後者の「事後分布からサンプルを得ること」です。 $p(D)$ を計算せずとも、事後分布に従うサンプルを得ることができれば、そのサンプル群から事後分布の特性(平均値、分散、分位数など)を近似的に推定することができます。
MCMC の基本アイデア:母集団と標本集団のイメージ
MCMC の基本的な考え方は、母集団と標本集団の関係に似ています。
- 母集団: 真に知りたい事後分布 $p(\theta | D)$ (しかし、計算は困難...)
- 標本集団: MCMC によって生成された、事後分布に従うサンプルの集まり
計算困難な事後分布 $p(\theta | D)$ を直接求める代わりに、$p(\theta | D)$ に従うサンプルを大量に生成し、そのサンプル集団(標本集団)から、逆に事後分布(母集団)を近似しようというのが、MCMC の基本的なアイデアです。
メトロポリスヘイスティング法:事後分布の比率に着目したサンプリング
MCMC の代表的なアルゴリズムの一つが、メトロポリスヘイスティング法です。
メトロポリスヘイスティング法は、「事後分布の比率が分かれば、サンプルを生成できる!」というアイデアに基づいています。
事後分布の比率を利用する
メトロポリスヘイスティング法では、以下の事後分布の比に着目します。
\begin{aligned}
\frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)}
&=
\frac
{p(D|\theta^{\ast})p(\theta^{\ast})/p(D)}
{p(D|\theta^{(t)})p(\theta^{(t)})/p(D)} \\
&= \frac{p(D|\theta^{\ast})p(\theta^{\ast})}{p(D|\theta^{(t)})p(\theta^{(t)})} \qquad (\because 分母 p(D) がキャンセルされる!)
\end{aligned}
重要な点は、事後分布の比を計算する際に、分母 $p(D)$ が分子と分母で相殺されるため、計算する必要がなくなるということです! これにより、分母の計算困難性という問題を回避しつつ、事後分布に関する情報を得ることが可能になります。
メトロポリスヘイスティング法のアルゴリズム
メトロポリスヘイスティング法のアルゴリズムは、以下のステップを繰り返すことで、事後分布からのサンプル $\theta^{(t)}$ を生成します。
-
提案: 現在のパラメータ $\theta^{(t)}$ をもとに、次のパラメータ候補 $\theta^{\ast}$ を提案分布 $q(\theta^{\ast}|\theta^{(t)})$ から生成します。
-
受理確率の計算: 受理確率 $a$ を以下の式で計算します。
$$
a = min\left(1,
\frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)}
\frac{q(\theta^{(t)}|\theta^{\ast})}{q(\theta^{\ast}|\theta^{(t)})}
\right)
$$ -
受理判定: $[0,1]$ の一様分布から乱数 $u$ を生成し、乱数 $u$ と受理確率 $a$ の大小を比較します。
- $u \leq a$ の場合:提案 $\theta^{\ast}$ を受理し、 $\theta^{(t+1)} = \theta^{\ast}$ とします。
- $u > a$ の場合:提案 $\theta^{\ast}$ を棄却し、 $\theta^{(t+1)} = \theta^{(t)}$ (現在のパラメータを維持)とします。
これらのステップを繰り返すことで得られるパラメータ列 ${ \theta^{(1)}, \theta^{(2)}, \theta^{(3)}, ... , \theta^{(N)} }$ が、事後分布 $p(\theta|D)$ からのサンプルとみなされます。
例①:レストランの人気度調査
メトロポリスヘイスティング法の基本的な流れを理解するために、簡単な例としてレストランの人気度調査を考えてみましょう。
設定
A, B, C の3つのレストランがあり、以下の人気度に関する情報のみが分かっているとします。
- A は B の 2 倍人気
- B は C の 3 倍人気
この情報から、各レストランの人気度 [A, B, C] = [60%, 30%, 10%] を MCMC 的に推定してみます。
MCMC の実行
ステップ 0: 初期値として、レストラン B を選択したとします。
ステップ 1:
-
現在のレストラン: B
-
提案されたレストラン: C
- どのようにして提案されるかについては後述します。いまは、3つのレストランから1つを選択してくれる便利な機械を使っていると思ってください。
-
受理確率の計算:
\begin{aligned} a &= min(1, \frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)}) \\ &= min(1, \frac{p(C)}{p(B)} \\ &= min(1, \frac{1}{3}) \\ &= \frac{1}{3} \end{aligned}
- ここで注意点。
- さっきは、受理確率を $a = min(1, \frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)}\frac{q(\theta^{(t)}|\theta^{\ast})}{q(\theta^{(\ast)}|\theta^{(t)})})$ としていましたが、ここでは、 $a = min(1, \frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)})$ としている点に注意です。これは上述したように複雑な部分を削ぎ落として、MCMCの計算の流れを掴むために、$\frac{q(\theta^{(t)}|\theta^{\ast})}{q(\theta^{(\ast)}|\theta^{(t)})}$ の計算を除外しています(そのほうがわかりやすいので)。後述しますが、これも大事な要素であるため、あとで正しいMCMCを計算するときにこれが復活させます。
- 一様乱数 $u = 0.5$ を生成
- $a < u$ なので、提案 C を棄却し、 $\theta^{(t+1)} = B$ (レストランは B のまま)
ステップ 2:
-
現在のレストラン: B
-
提案されたレストラン: A
-
受理確率の計算:
\begin{aligned} a &= min\left(1, \frac{p(A)}{p(B)}\right)\\ &= min\left(1, \frac{2}{1}\right)\\ &= 1 \end{aligned} -
一様乱数 $u = 0.2$ を生成
-
$u < a$ なので、提案 A を受理し、 $\theta^{(t+1)} = A$ (レストランは A に変更)
ステップ 3 - 5: 同様のステップを繰り返します。
結果、以下のようになったとします。
| ステップ | 現在地 | 提案 | 受理/棄却 |
|---|---|---|---|
| 1 | B | C | 棄却 |
| 2 | B | A | 受理 |
| 3 | A | B | 受理 |
| 4 | B | C | 受理 |
| 5 | C | B | 受理 |
MCMC の結果: 上記のステップを多数回繰り返すことで、各レストランが選択された回数を集計し、人気度を推定します。今回の例では、 [A, B, C] = [1/5, 3/5, 1/5] となりました。ステップ数が少ないため理論値とは異なる結果となりました。このステップ数を増やすことで理論値 [A, B, C] = [60%, 30%, 10%] に近づいていきます。
Python コードによる検証(ステップ数と精度)
import numpy as np
rng = np.random.default_rng()
import collections
# 遷移確率
prob_dict = {
("A","A"): 1., # A -> A
("A","B"): 1./2, # A -> B
("A","C"): 1./6, # A -> C
("B","A"): 1., # B -> A
("B","B"): 1., # B -> B
("B","C"): 1./3, # B -> C
("C","A"): 1., # C -> A
("C","B"): 1., # C -> B
("C","C"): 1., # C -> A
}
int2name={
0:"A",
1:"B",
2:"C",
}
def count_name(mcmc_results:list)->dict:
return collections.Counter(mcmc_results)
def get_suggestion() -> int:
"""generate suggestion
out: integer
"""
return rng.integers(low=0, high=3)
def mcmc(n:int = 100):
"""MCMCを実行する"""
res_hists = []
res_hists.append("B")
for _ in range(n):
current_name = res_hists[-1]
suggested_int = get_suggestion()
suggested_name = int2name[suggested_int]
# print(f"{current_name} --> {suggested_name}")
prob = prob_dict[(current_name, suggested_name)]
acceptance_ratio = min([1., prob])
u = rng.random()
# print(f"{prob=}", f"{acceptance_ratio=}", f"{u=}")
if u < acceptance_ratio:
res_hists.append(suggested_name)
else:
res_hists.append(current_name)
# delete init value
res_hists.pop(0)
return res_hists
# 10ステップ
res_hists = mcmc(n = 10)
count_name(res_hists)
# 出力
# Counter({'B': 5, 'A': 3, 'C': 2})
# 100ステップ
res_hists = mcmc(n = 100)
count_name(res_hists)
# 出力
# Counter({'A': 48, 'B': 33, 'C': 19})
# 1000ステップ
res_hists = mcmc(n = 1_000)
count_name(res_hists)
# 出力
# Counter({'A': 596, 'B': 304, 'C': 100})
# 10000ステップ
res_hists = mcmc(n = 10_000)
count_name(res_hists)
# 出力
# Counter({'A': 5989, 'B': 3038, 'C': 973})
上記の Python コードを実行すると、ステップ数を増やすほど、MCMC による推定結果が理論値 [60%, 30%, 10%] に近づくことが確認できます。
(もしコピペして実行させても、上記のコードのままでは乱数のseedを固定していないので、上記の結果と同じ数値が出てこないかもしれないです。)
例②:1次元ガウス分布の平均推定
より実務に近い例として、1次元ガウス分布の平均 $\mu$ を MCMC で推定するケースを考えます。分散 $\sigma$ は既知(だったとします。)とし、観測データは ${x_1, x_2}$ の2点のみと仮定します。さらにパラメータ$\mu$の事前分布の平均値は$m$として設定しておきます。
ちなみに$\sigma$が未知だったとしても$\mu$と$\sigma$を推定するためにちょうど良い事前分布がすでに存在している(知られている)ので、それを使えば下記のアルゴリズムで$\mu$と$\sigma$それぞれの事後分布を近似できます。今回のケースは説明用に使いやすい$\mu$を推定するケースを考えます。この場合は、ガウス分布を事前分布に設定すれば良いと経験的にわかっているので、説明しやすいです。
モデル設定
- 事前分布: $p(\mu) = N(\mu|m,\sigma_{\mu}^2)$ (平均 $m$、分散 $\sigma_{\mu}^2$ のガウス分布)
- 尤度: $p(x_i|\mu) = N(x_i|\mu, \sigma^2)$ (平均 $\mu$、分散 $\sigma^2$ のガウス分布)
例①のMCMCのアルゴリズムで厄介そうなのは、受理確率の計算ですよね。これが計算可能なものなのかMCMCする前に、確認してみましょう。
受理確率の計算
事後分布の比は、以下のように計算できます。
\begin{aligned}
\frac{p(\mu^{\ast}|D)}{p(\mu^{(t)}|D)}
&=
\frac
{p(D|\mu^{\ast})p(\mu^{\ast})/p(D)}
{p(D|\mu^{(t)})p(\mu^{(t)})/p(D)} \\
&= \frac{p(D|\mu^{\ast})p(\mu^{\ast})}{p(D|\mu^{(t)})p(\mu^{(t)})} \\
&= \frac{ p(\mu^{\ast}) p(x_1|\mu^{\ast})p(x_2|\mu^{\ast}) }{ p(\mu^{(t)}) p(x_1|\mu^{(t)})p(x_2|\mu^{(t)}) } \\
&= \frac{
\frac{1}{\sqrt{2\pi \sigma_{\mu}^2} }
exp\left(- \frac{ (\mu^{\ast} - m)^2}{2\sigma_{\mu}^2}\right)
\times
\frac{1}{\sqrt{2\pi \sigma^2} }
exp\left(- \frac{ (x_1 - \mu^{\ast})^2}{2\sigma^2}\right)
\times
\frac{1}{\sqrt{2\pi \sigma^2} }
exp\left(- \frac{ (x_2 - \mu^{\ast})^2}{2\sigma^2}\right)
}
{
\frac{1}{\sqrt{2\pi \sigma_{\mu}^2} }
exp\left(- \frac{ (\mu^{(t)} - m)^2}{2\sigma_{\mu}^2}\right)
\times
\frac{1}{\sqrt{2\pi \sigma^2} }
exp\left(- \frac{ (x_1 - \mu^{(t)})^2}{2\sigma^2}\right)
\times
\frac{1}{\sqrt{2\pi \sigma^2} }
exp\left(- \frac{ (x_2 - \mu^{(t)})^2}{2\sigma^2}\right)
}
\end{aligned}
上記の式は、すべてのパラメータ ($\sigma_{\mu}^2, \sigma^2, m, x_1, x_2, \mu^{(t)}, \mu^{\ast}$) が既知であれば、スカラ値として計算可能です。
実際、$\mu^{(t)}$は各ステップで定義されます(ステップ1であれば初期値 $\theta^{(0)}$)。
さらに、$\mu^{\ast}$は各ステップで提案されたパラメータ値なのでアルゴリズム中で既知のものとなります。
$x_1$:観測データなのでわかっています。
$x_2$:観測データなのでわかっています。
また$m$は事前分布として設定しているので、これも既知として扱えます。
以上から、上記の計算は手でやると大変ですが、計算するための値がすべて既知であるため、比率を(例えば0.8のような)値として出すことができます。
MCMC のステップ
- ステップ 0: 初期値 $\mu^{(0)}$ を適当に設定します。
-
ステップ 1:
- 現在のパラメータ値: $\mu^{(t)} = \mu^{(0)}$
- 提案されたパラメータ値: $\mu^{\ast}$ (提案分布から生成)
- 受理確率 $a$ を上記式で計算
- 一様乱数 $u \quad \in[0,1]$ を生成
- $u \leq a$ ならば $\mu^{(t+1)} = \mu^{\ast}$、そうでなければ $\mu^{(t+1)} = \mu^{(t)}$
- ステップ 2 以降: ステップ 1 を繰り返します。
MCMC の結果: MCMC を実行することで、パラメータ $\mu$ のサンプル列 ${ \mu^{(1)}, \mu^{(2)}, \mu^{(3)}, ... , \mu^{(N)} }$ が得られます。このサンプル列を用いて、事後分布の特性を分析します。
例えばN=5だったとしたら以下のような結果となります。
| ステップ | 現在地 | 提案 | 受理したかどうか |
|---|---|---|---|
| 1 | θ^(1) = θ^(0) | θ^*_1 | 受理 |
| 2 | θ^(2) = θ^*_1 | θ^*_2 | 棄却 |
| 3 | θ^(3) = θ^(1) | θ^*_3 | 受理 |
| 4 | θ^(4) = θ^*_3 | θ^*_4 | 受理 |
| 5 | θ^(5) = θ^*_4 | θ^*_5 | 棄却 |
注意点: MCMC の初期段階のサンプルは、初期値に依存する傾向があるため、一般的にはバーンイン期間として初期のサンプルを破棄し、後半のサンプルのみを分析に用います。
補足:受理確率の意味
受理確率 $a = min\left(1, \frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)}\right)$ の$\frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)}$は、提案パラメータ $\theta^{\ast}$ が現在のパラメータ $\theta^{(t)}$ よりも、真の事後分布に近いかどうかを計算したものです。
- $\frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)} \geq 1$ の場合:提案 $\theta^{\ast}$ は現在の $\theta^{(t)}$ よりも事後分布に近いと判断され、100% の確率で受理されます。
- $\frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)} < 1$ の場合:提案 $\theta^{\ast}$ が事後分布に近い確率に応じて、確率的に受理されます。
確率的に受理する理由は、MCMC が事後分布そのものを近似することを目的としているためです。分布を近似するためには、取りうるパラメータ値の範囲を網羅的にサンプリングし、かつ、事後分布の形状を反映した頻度で各パラメータ値が出現するようにする必要があります。確率的な受理ステップは、この要請を満たすために不可欠な仕組みです。
ここは筆者がなぜ一定確率で、真の事後分布から遠ざかる方のパラメータも受理するのか不思議に思ったので、ChatGPTに聞いたり調べながら着地した結論です。
$\frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)}$ は要するに、 $p(\theta^{\ast}|D)$ と $p(\theta^{(t)}|D)$ のどっちのほうが、真の分布に近いのかを表したものである。
であるとするならば、 $\frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)} >= 1$ のとき(つまり提案パラメータ $\theta^{\ast}$ のほうが真の分布に近い)に100%の確率で提案パラメータを受理するのは直感的に理解できる。なぜなら、本来の分布を近似することが目的なので、現在値( $\theta^{(t)}$)よりも 本来の分布により近いであろう $\theta^{\ast}$ を受理するのは自然である。
しかし、 $\frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)} < 1$ のときは確率的に提案パラメータを受領するのはなぜなのか?
これは、MCMCの目的が関係している。
MCMCの目的は、事後”分布”をサンプルから近似(推測)することが目的であった。キーワードは”分布”である。
分布である以上、取りうる値のすべてを網羅している必要がある。
そしてその値の出現頻度は、もとの分布(=真の事後分布)で高頻度で出現する値はサンプル(MCMCの結果)上でも高頻度に出現し、
もとの分布(=真の事後分布)で低頻度でしか出現しない値はサンプル(MCMCの結果)上でも低頻度に出現しない
を再現しないといけない。
これを実現するために、 $\frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)} < 1$ であったとしても確率的にその 提案値を受理する、というステップを踏んでいる。
おまけ | MCMCで取得したパラメータサンプル(パラメータ分布)の活用方法
MCMCのアルゴリズムには直接関係ないので、読み飛ばしてもOK。MCMCをやったところで何に使えるのかを説明している。
- いろいろなことに使える。
- 事後分布の可視化。
- 事後分布を計算的に求められないから困っていたが、 MCMCの結果、得られたパラメータサンプルをKDEなりヒストグラムなりの処理に突っ込めば分布を可視化することができる。
- 事後平均や信頼区間の計算
- 事後分布の可視化。
事後平均の計算の仕方
$E[x^{\ast}]$ を求める、ということ。
上記の例のケースの場合は、
\begin{aligned}
p(x^{\ast}|x_1, x_2)
&= \int p(x^{\ast}|\mu) p(\mu|x_1, x_2) d\mu
\end{aligned}
この中で、 $p(\mu|x_1, x_2)$ はMCMCで擬似的に求めたものである。したがって、期待値の計算は、
\begin{aligned}
E[x^{\ast}]
&= \int x^{\ast}p(x^{\ast}|x_1, x_2) dx^{\ast}\\
&\approx
\frac{1}{N}\sum^{N}_{i=1}E[x^{\ast}|\mu_i]
\end{aligned}
ここで、
\begin{aligned}
E[x^{\ast}|\mu_i]
&= \int x^{\ast} N(x^{\ast}|\mu_i, \sigma^2) d\mu \\
&=\mu_i
\end{aligned}
であるので、事後平均は、サンプリングされたN個のパラメータ( $\mu_i$)の平均に等しいことがわかった。
正しい受理確率の定義:提案分布の考慮
ここまでの説明では、受理確率を $a = min\left(1, \frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)}\right)$ としてきましたが、正しいメトロポリスヘイスティング法における受理確率の定義は、以下の通りです(これまでの計算の仕方はMCMCの流れを理解しやすくするために正しくない定義で計算してました)。
$$
a = min\left(1,
\frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)}
\frac{q(\theta^{(t)}|\theta^{\ast})}{q(\theta^{\ast}|\theta^{(t)})}
\right)
$$
ここで、 $q(\theta^{\ast}|\theta^{(t)})$ は提案分布と呼ばれ、現在のパラメータ $\theta^{(t)}$ から次の候補 $\theta^{\ast}$ を提案する際の確率分布を表します。 $\frac{q(\theta^{(t)}|\theta^{\ast})}{q(\theta^{\ast}|\theta^{(t)})}$ は、提案分布の比率であり、提案分布の形状が非対称である場合に、サンプリングの偏りを補正する役割を果たします。
非対称な提案分布の問題点
例えば、ポアソン分布や指数分布のように非対称な形状を持つ提案分布を用いる場合、パラメータ空間のある方向に提案されやすく、別の方向には提案されにくいという偏りが生じることがあります。
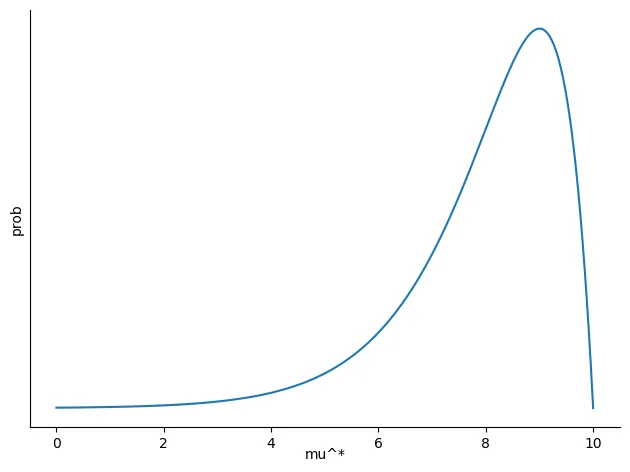
このような偏りが生じると、受理確率 $a = min\left(1, \frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)}\right)$ のみを用いた場合、提案分布で高頻度に提案されるパラメータ領域ばかりが重点的にサンプリングされ、パラメータ空間全体を網羅的にサンプリングできなくなる可能性があります。
提案分布の比率による補正
提案分布の比率 $\frac{q(\theta^{(t)}|\theta^{\ast})}{q(\theta^{\ast}|\theta^{(t)})}$ を受理確率に掛け合わせることで、非対称な提案分布を用いた場合に生じるサンプリングの偏りを軽減することができます。
- $\theta^{(t)} < \theta^{\ast}$ の場合: 提案分布において $\theta^{\ast}$ が提案されやすい場合、 $\frac{q(\theta^{(t)}|\theta^{\ast})}{q(\theta^{\ast}|\theta^{(t)})} < 1$ となり、受理確率が抑制されます (ペナルティ)。
- $\theta^{\ast} < \theta^{(t)}$ の場合: 提案分布において $\theta^{\ast}$ が提案されにくい場合、 $\frac{q(\theta^{(t)}|\theta^{\ast})}{q(\theta^{\ast}|\theta^{(t)})} > 1$ となり、受理確率が増加します (報酬)。
このように、提案分布の比率を考慮することで、非対称な提案分布を用いた場合でも、よりバランスの取れたサンプリングを実現し、事後分布の近似精度を向上させることができます。
私が提案分布の比を事後分布の比に掛け算している理由を勉強していたときのメモも残しておく
問題意識
結論、以下で受理確率を計算するとMCMCとして都合が悪いのである。
\frac
{
p(\theta^{\ast}|D)
}
{
p(\theta^{(t)}|D)
}
- MCMCは、「任意の分布からサンプルを生成できること」に本質がある。
- これを考えたときに、ある特徴を持つ提案分布を使うと都合悪いのである。それは、非対称な形状を持つ提案分布である。非対称な分布を持つ分布とは、ポアソン分布や指数分布などである。逆に対称な形を持つ分布は例えばガウス分布や一様分布である。
- 結論から言えば、この非対称な形状の提案分布を想定したときに、以下のように提案分布の比( $\frac{q(\theta^{(t)}|\theta^{\ast})}{q(\theta^{(\ast)}|\theta^{(t)})}$)を掛け算してあげると、非対称さによる悪影響を軽減(言い換えると、非対称な分布を使ったときの提案パラメータに対してペナルティをかけられる)できるのである。
\frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)}
\frac{q(\theta^{(t)}|\theta^{\ast})}{q(\theta^{(\ast)}|\theta^{(t)})}
- このようなペナルティ項をかけたときに対称な分布のときに問題とならないのか気になるだろうが、問題ない。なぜならば、対称な分布のときは、 $\frac{q(\theta^{(t)}|\theta^{\ast})}{q(\theta^{(\ast)}|\theta^{(t)})} = 1$ となるためだ。
非対称な分布を持つときの問題

- この分布のとき $\theta^{\ast}$ は、比較的大きな値(8~9)隣りやすい一方で、小さい値(0~4)は取りづらい。つまり、大きな値ばっかり提案されやすいということ。逆に小さい値は提案されづらい。
- 「パラメータ値が 右側に行きやすいのに、左側には行きづらい」という状況。- つまり提案分布の時点で提案されてくる パラメータ値( $\theta^{\ast}$)が特定領域に偏ってしまっているということ。
- こうなると、 $a = min(1, \frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)})$ で計算される受理確率は、提案分布で偏っているパラメータ範囲(8~9)だけ集中して受理する( & 棄却する)することとなってしまい、取りうるパラメータ範囲全部のサンプリングが行えくなってしまう。
- ここまで読んでいると、そもそも非対称な提案分布を使わなければ良いのではないかと思ったのではないだろうか。私も思った。
- しかし、調べると、一部の問題だとこういう非対称な分布を使ったほうが良いケース(ロジスティック回帰の係数の分布とか)がある模様。また、離散値の分布を考えるときなど、対称な形の分布を使えないケースもあるため、非対称な提案分布を使ったときの補正が必要なのだそうだ。- では、メトロポリスヘイスティング法の場合は、この問題を軽減するために何をするのかといえば、提案分布の比を事後分布の比に掛け算するのである。
- $\theta^{(t)} < \theta^{\ast}$ のとき、 $q(\theta^{(\ast)}|\theta^{(t)}) > q(\theta^{(t)}|\theta^{\ast})$ である。
- これは、提案分布において、大きな値ほど高頻度で提案されやすいという回避すべき状態である。ペナルティを与えたい。- $\theta^{\ast} < \theta^{(t)}$ のとき、 $q(\theta^{(\ast)}|\theta^{(t)}) < q(\theta^{(t)}|\theta^{\ast})$ である。
- これは、 珍しく、小さな値が提案された状態である。ペナルティではなく、報酬を与えたい。- これを考えると、 $\frac{q(\theta^{(t)}|\theta^{\ast})}{q(\theta^{(\ast)}|\theta^{(t)})}$ という比率でペナルティ(もしくは報酬)を与えると良さそう、という見通しが立つ。
- 実際に受理確率の定義を見てみると、 $a = min(1, \frac{p(\theta^{\ast}|D)}{p(\theta^{(t)}|D)}\frac{q(\theta^{(t)}|\theta^{\ast})}{q(\theta^{(\ast)}|\theta^{(t)})})$ となっている。
まとめ
- MCMCの中でもメトロポリスヘイスティング法に絞って説明しました。
- 個人的にこう解釈すると理解しやすい、というものを噛み砕いて説明してみましたが、数式ばっかりになってしまいました。
- 個人的にMCMCを勉強していると、「詳細釣り合い条件」とか「遷移核」とかそういった用語や概念が出てきて、最終目標である "サンプリングしたい!" との関連性が見えず、混乱していました。事後分布を直接計算できないから変わりにサンプリングして代用しよう、という発想のはずなのに、詳細釣り合い条件?遷移核? サンプリングしたい、という考えはどこいった?となってました。しかし、以下のように割り切って整理するとわかりやすいと思いました。
- MCMCの本質的なところは、事後分布の分母を計算しなくて済むように比率で計算しているところにある。推定したいパラメータ(の新しい)値が提案されたとき、そのパラメータと現在のパラメータとで事後分布をそれぞれ計算して、大きければ即採用。小さければ確率的に(あえて)採用する。
- つまり、『提案分布の条件はあくまでも、補正のために使用しているだけであり、本質は事後分布の比でサンプリングしている点』と捉えてしまうと、 すっと理解できました。